Sonia Sorgato, classe seconda, Milano
“Sei stato bravissimo a spiegarmi come contare i pezzi del puzzle, anche se non si vedevano tutti.” (Davide, 7 anni)
Ci troviamo ad affrontare in questi giorni un’esperienza di scuola totalmente diversa che non può far leva su tutti gli aspetti che solitamente caratterizzano il modo di stare a scuola: la relazione, le routine, la cooperazione.
Per questo ci è sembrato prioritario fin dai primi momenti salvare dalle modalità consolidate le pratiche che hanno caratterizzato il lavoro di quest’anno per fare in modo che la didattica a distanza non venisse travolta dai metodi trasmissivi che sono sicuramente i più facili da realizzare in una situazione di emergenza. Questa priorità risponde anche al bisogno delle insegnanti e dei bambini di trovare in questi momenti pezzi di normalità anche in ciò che normale non è. Per rispondere a questo bisogno abbiamo chiesto ai bambini di continuare a inviarci le loro creazioni matematiche. Il lavoro sulle creazioni matematiche nasce dalla lettura del testo di Le Bohec (Il testo libero di matematica) e dai corsi del MCE a Cantieri e a Milano tenuti da Donatella Merlo e Valeria Perotti.
Per Le Bohec una creazione matematica “È semplice, è una qualsiasi cosa! Allora ecco: a partire da cifre, da numeri, da punti o da lettere (cioè segni), componete una cosa qualsiasi. Questa qualsiasi cosa tutti sono capaci di farla”. Le Bohec sottolinea che “è ugualmente nella natura dell’uomo cercare di dare un ordine alle cose che lo circondano. […] Si tratta di dare un ordine al mondo esterno. Questo sarebbe invivibile se, a poco a poco, non se ne scoprissero le leggi, se non si imparassero a distinguervi delle strutture per proteggersene meglio o meglio dominarlo. Questa funzione di comprensione si esercita molto presto nella vita” (Le Bohec, 1985). A partire dalla capacità dei bambini di comprendere, rappresentare e scoprire le regole che dominano gli oggetti e i fenomeni del mondo è stato avviato in questo anno scolastico un lavoro che ha permesso di orientare la progettazione di classe, che ha determinato i passaggi e le proposte poiché i prodotti dei bambini e le discussioni che ne sono seguite durante il percorso hanno evidenziato il punto in cui si trovavano e il loro bisogni formativi. Come esempio di questa situazione possiamo analizzare le creazioni matematiche di Ginevra e Cloe e di Jan Paul che ci mostrano una teorizzazione del calcolo in colonna non ancora affrontato in modo sistematico e nella seconda creazione un avvio alla moltiplicazione. Queste due creazioni, insieme alle altre, hanno permesso di orientare i percorsi a partire dalle conoscenze e dalle prime forme di concettualizzazione che hanno trovato una risonanza all’interno del gruppo classe così come emerge da questa discussione:
Sara: in quella di Jan Paul vedo che ha scritto tanto e ha fatto un disegno.
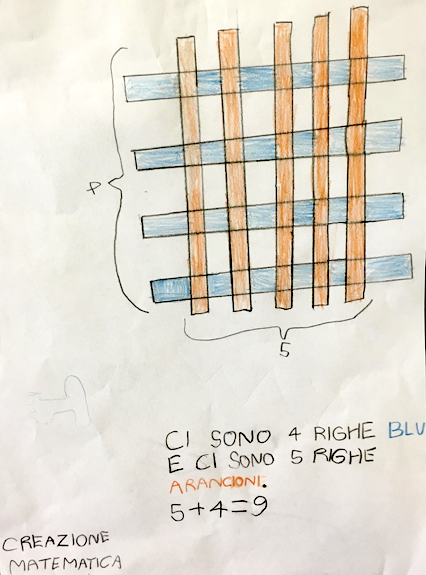
Alessandro: in quella di Jan Paul ha messo delle linee blu e delle linee arancioni, ha scritto il numero 4 e il numero 5, ha fatto un’operazione e ha scritto come si fa, ha scritto un’operazione con i numeri e con le parole…
Sonia: un’operazione con le parole…
Davide: quelle righe che ha fatto Jan sembrano delle operazioni in colonna.
Cloe: Jan ha scritto che ci sono 4 righe blu e 5 righe arancioni e se tu le conti tutte insieme fanno 9.
Ale: ha contato le righe e ha visto che faceva 9. 4+4+1 fa 9.
Matteo: c’è un’operazione con le parole ed è un problema difficile come quelli che abbiamo ma con la risoluzione già fatta, è come se fosse una scheda autocorrettiva perché c’è già la risposta.
Arianna: in quella di Jan mi sembra che ci sono unità e decine e ha fatto 4 e 5 che fa 9.
Sveva: in quella di Jan Paul vedo pochi numeri.
Stefany: io vedo dei quadretti arancioni e blu.
Sonia: Stefany ha notato una cosa nuova.
Matteo: ci sono delle righe che vanno una sopra l’altra.
Alessandro: ci sono degli incroci, una riga va sopra l’altra.
Jan Paul: per fare questa creazione matematica ho disegnato 4 righe e ho scritto il numero 4, poi ho disegnato altre 5 righe e ho scritto il numero 5 qui, ho scritto l’operazione e ho usato i colori.

In questo momento segnato da giornate senza scuola ci sembra prioritario proseguire il lavoro per fare in modo che i bambini continuino a cercare e a rappresentare le proprie idee nei confronti dei concetti matematici: per questo abbiamo richiesto di inviarci le loro creazioni matematiche. Così come accade in classe è di fondamentale importanza “non lasciare il fanciullo alle sole proprie risorse” (Le Bohec, 1985). Ciò che è emerso nelle creazioni inviate da casa è la capacità dei bambini di trovare le strutture matematiche nella loro vita quotidiana, nei giochi come il lego, i puzzle, i giochi di costruzione, negli oggetti quotidiani, nelle pratiche sperimentate come le ricette in cucina (video che posso condividere: lego). Le loro teorie rispetto alle strutture condivise in una bacheca virtuale (così come facciamo realmente in classe con un cartellone) hanno animato gli scambi di questi giorni: i bambini hanno commentato i lavori dei compagni, ma aspetto ancora più significativo, le creazioni successive sono state influenzate da quelle prodotte dai compagni. Se analizziamo la creazione di Davide notiamo che la sua costruzione con dei mattoncini di legno riproduce una scala il cui punto più alto è formato da 10 pezzi, il gradino più in basso da 9 pezzi, poi 8, 7 e così via. Si tratta di una costruzione molto interessante perché mette in luce la successione numerica e l’ordine dei numeri: essi vengono riconosciuti all’interno di un gioco o forse è a partire da questa consapevolezza matematica che prende vita la costruzione stessa o più probabilmente c’è un’interazione tra i due piani. Sulla bacheca virtuale abbiamo restituito al bambino una domanda per tutta la classe: quanti pezzi sono stati utilizzati in tutto?
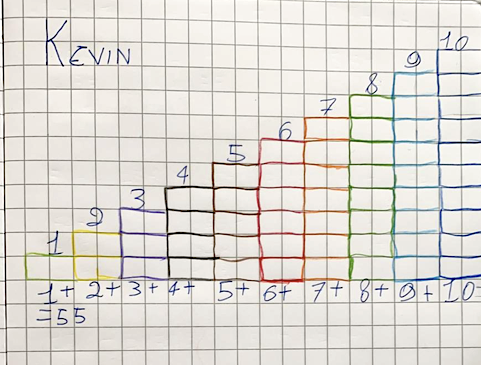
L’idea successiva è quella di ampliare questa domanda a numeri più grandi per lavorare su strategie più veloci per il calcolo (magari come Gauss). Le prime risposte stanno già arrivando e rivelano una circolarità che si concretizza in rappresentazioni in grado di riprendere la costruzione del compagno mettendone in evidenzia le caratteristiche geometriche e numeriche. La creazione di Davide ha dato spunto a un altro video di una compagna che ha ripreso il tema della successione numerica per rappresentare concretamente con delle custodie di dvd una struttura a triangolo per un totale di 15 custodie. La successione numerica, la sua rappresentazione, il riconoscimento di questa struttura negli oggetti della quotidianità sembrano rimbalzare di casa in casa, ogni bambino aggiunge un aspetto o ne dispiega uno in particolare.

Un altro filo rosso che caratterizza le creazioni matematiche inviate questi giorni è la struttura moltiplicativa: emerge il bisogno dei bambini di tornare sui percorsi avviati in classe a partire dal reticolo di Jan Paul. Nel video qui presente Antonio descrive un pezzo di Lego 8×4 da 32. Successivamente vengono sovrapposti a questo primo pezzo 2 pezzi da 16 (2×8) e poi 4 pezzi (4×2) e infine 8 pezzi (2×2).

In questa creazione matematica si mette in evidenza la struttura della moltiplicazione in modo molto chiaro e Antonio permette a tutti i compagni un aggancio concreto con ciò che utilizzano per giocare. L’invito è quello di riflettere sugli oggetti e la risposta non tarda ad arrivare. In un video successivo un compagno presenta un puzzle: il bambino costruisce solo la metà della cornice in verticale e in orizzontale. Sotto alla cornice viene riprodotta la numerazione che permette di contare i pezzi necessari per delimitare i due lati del puzzle. Giorgio esplicita il fatto di aver trovato il modo di contare tutti i pezzi senza contarli uno a uno e per argomentare questa affermazione fa riferimento al reticolo numerato e mostra come sia possibile scoprire il numero dei pezzi contando le colonne e procedendo di 10 in 10.

In questo momento il ruolo dell’insegnante è quello di rilanciare e ampliare ciò che portano i bambini per estendere ancora di più queste scoperte e trovare nuovi elementi in ciò che sperimentano. Le creazioni permettono di tenere viva la loro attenzione nei confronti delle strutture matematiche e consentono di creare una continuità rispetto alla progettazione in grado di partire dalla realtà di ciò che osservano per trovare agganci con i loro interessi. L’idea che guida questa proposta è quella di trasformare queste ipotesi e ricerche individuali in un bene collettivo, in conoscenze di classe.
Dalle creazioni matematiche nascono in particolare due piste di lavoro: una su pattern e regolarità (pre-algebra) e una sulle strutture moltiplicative.
