Enrico Bottero

La pedagogia Freinet ha un punto fermo: il rifiuto della “scolastica”. Questo rifiuto l’ha indotta a privilegiare la pedagogia del progetto concretizzatasi nelle diverse tecniche di vita: testo libero, giornale, corrispondenza interscolastica, ecc. In questo modo non si vuol rinunciare a far apprendere i saperi ma li si persegue indirettamente grazie a un progetto finalizzato e motivante (il testo libero, ad esempio, può condurre a riflessioni sulla lingua, al miglioramento dell’ortografia, a ricerche scientifiche e di ambiente e a molto altro).  Si cercano così di comporre due  esigenze pedagogiche:  dare un senso a quello che si fa a scuola e far progredire gli apprendimenti. Sappiamo però che questa  è una via non facile perché ci costringe a  restare sempre su un crinale (1). Ma non dobbiamo stupircene: stare sul crinale è il destino di ogni buona pedagogia che cerca di conciliare  esigenze apparentemente in contrasto tra loro. Naturalmente, come in ogni azione educativa, non mancano i rischi. Ad esempio, c’è il rischio che l’attività cada in una deriva “produttivista”: si lavora per fare un buon prodotto senza aver necessariamente appreso. Spesso la logica dell’efficacia non permette di arrivare alla comprensione. L’essere umano, adulto o minore, tende infatti a cercare  un risultato con il minimo sforzo. Tutto ciò non è in sé un fatto negativo: ogni attività produttiva si trova costretta ad adottare questa postura. È una postura, però, che contraddice le finalità della scuola. A scuola, infatti, non si va solo per “fare”  qualcosa ma anche per acquisire un “sapere”. Dunque, come perseguire gli apprendimenti senza abbandonare le “tecniche di vita”? Come non abbandonare i ragazzi  più in difficoltà  evitando che producano qualcosa senza  aver appreso? La scelta di Freinet è stata chiara: l’individualizzazione attraverso il sistema del piano di lavoro e dei brevetti. Con questa scelta  non ha rinunciato ad un principio cardine: scommettere sull’autonomiadel ragazzo coinvolgendolo nella definizione di attività e obiettivi individualizzati, concedendogli un potere decisionale nella scelta delle attivitàe  dei tempi della loro valutazione. La personalizzazione degli apprendimenti deve permettere al ragazzo di lavorare in funzione dei suoi bisogni ed interessi facendo di lui l’attore della propria formazione. Non a caso, con il piano di lavoro si personalizzano  molte attività, non solo le esercitazioni di lingua e matematica, ma anche la ricerca e i testi liberi. Con il sistema dei brevetti, poi, si cerca di fare in modo che tutti gli allievi, in tempi medio-lunghi, possano raggiungere gli obiettivi di apprendimento fondamentali. È la valutazione per “unità di valore” che va a sostituire le tradizionali valutazioni sommativa e certificativa.

Con queste scelte la pedagogia Freinet non ha affatto abbandonato la centralità del progetto, anzi. Il piano di lavoro, cioè, non è una pedagogia per obiettivi individualizzata in cui l’insegnante, individuato il livello di apprendimento di ciascun allievo, gli assegna un compito per quella settimana offrendogli un feed back in fase finale.  Non è, insomma, una valutazione formativa à la Scriven. Il punto di partenza, infatti, è sempre l’autonoma scelta di attività che abbiano un senso per l’allievo (finalizzazione). Naturalmente, con gradualità, nel dialogo insegnante – allievo e tra allievi (utilizzando altre “istituzioni”, l’aiuto reciproco e il tutorato), il ragazzo si rende consapevole degli obiettivi di apprendimento legati all’attività (obiettivi che l’insegnante già conosce). In questo modo la sua autovalutazione si affina e si perfeziona fino a permettergli di autoregolarsi e scegliere con maggior consapevolezza le attività da svolgere nella settimana successiva. 

Le attività individualizzate sono uno dei modi con cui, in tempi e modalità diverse, si perseguono gli apprendimenti di tutti. Non va infatti dimenticato che hanno senso solo se si collocano in un sistema di classe cooperativa. L’auto-organizzazione dei ragazzi e il lavoro comunitario a scopo sociale sono alla base del vivere e dell’apprendere insieme.

(1) Non è un caso che Sul crinale sia il titolo della prima parte del volume di Philippe Meirieu Una scuola per l’emancipazione (Roma, Armando, 2019)

Per approfondire v.  https://www.enricobottero.com/pedagogia-freinet; https://www.icem-pedagogie-freinet.org/node/14228. 

Nessun tag per questo articolo.

Materiali per un piano di lavoro

Abbiamo già condiviso il modello di piano di lavoro usato da Freinet a Vence in un articolo precedente (per saperne di più: Bibliothèque de l’Ecole Moderne n° 15 – Les plans de travail | Coop’ICEM.pdf). Si legge, nelle proposte di questo piano, l’idea dei “complessi d’interesse” a cui si ispirava Freinet e anche l’importanza data al lavoro e alle attività manuali.
Praticamente sono i “compiti” che ogni alunno progetta di svolgere da solo durante una settimana. Ma come fa un alunno a decidere che cosa inserire nel suo piano di lavoro?
Lo ricava, su indicazione del maestro, dal percorso didattico svolto in classe nella settimana precedente, il quale, a sua volta, fa parte del piano annuale relativo ad ogni disciplina. È l’insegnante che predispone un piano generale delle attività. L’allievo compone il suo piano di lavoro personale scegliendo tra le opzioni che gli presenta l’insegnante. Poi, deve essere libero di svolgere il lavoro nei tempi e nei modi stabiliti dall’organizzazione della classe cooperativa, anche non in presenza dell’insegnante della disciplina a cui si riferisce il compito. Nel piano sono previste sia attività di consolidamento delle abilità strumentali sia attività di studio sia attività creative e rilassanti e, a fine settimana, c’è sempre un momento anche breve di dialogo insegnante/alunno in cui si fa un bilancio del lavoro effettivamente svolto e si mettono in luce gli obiettivi ancora da raggiungere.

• 

• 

Nei piani di lavoro che condividiamo ora della classe di Sonia Sorgato (molti altri a cui ispirarsi sono reperibili sui siti francesi) non tutte le attività sono autocorrettive, lo sono solo le schede di italiano e di matematica; nel piano ci sono le tecniche (la corrispondenza scolastica, le creazioni matematiche, il testo libero); le attività cambiano di settimana in settimana anche in base a nuovi interessi che si creano nella classe; c’è l’autovalutazione e la riflessione metacognitiva; c’è la firma del genitore. In questo piano di lavoro inizialmente c’erano attività solo di italiano e matematica ma gradualmente nella classe si sono introdotte anche altre discipline e altre attività (inglese e lavoro manuale) e poi, in futuro, ci saranno anche le conferenze degli alunni su un tema scelto per lo studio personale.

Dal piano di lavoro emerge la coerenza e l’integrazione tra questo strumento e le altre tecniche oltre agli aspetti relativi all’autovalutazione che è uno dei primi passi per condurre l’allievo a costruirsi strumenti di autoregolazione necessari per poter dire di avere imparato e anche di avere imparato ad imparare. Dare in mano ai bambini un “documento” di questo tipo, cartaceo e strutturato secondo un preciso impianto metodologico, significa istituzionalizzare il momento del lavoro autonomo, dargli valore e rilevanza all’interno delle attività della classe. Significa anche dare fiducia ai bambini, credere nelle loro capacità e quindi potenziare l’autostima, oltre a condividere con loro, in ogni momento dell’attività scolastica, gli obiettivi di apprendimento. Dall’organizzazione del documento si desume quindi in gran parte il modo di lavorare della classe.

Allora che fare? Un primo passo, per andare nella direzione del materialismo pedagogico, potrebbe essere riprendere in mano i vecchi materiali ad esempio gli schedari autocorrettivi MCE per il calcolo e l’ortografia. Erano materiali che non implicavano necessariamente un metodo particolare di lavoro per poter essere fruiti, li potevano usare tutti ed erano tutti autocorrettivi, gli obiettivi erano semplici ed espliciti.

• 

• 

• 

• 

Lo schedario di calcolo era determinato dalla tecnica freinetiana del “calcolo vivente” e quindi dalla necessità di esercitarsi sul “far di conto”, funzionale però alla risoluzione dei problemi posti quotidianamente dalla classe cooperativa. 
Lo stesso valeva per lo schedario di ortografia: dovendo scrivere e poi diffondere un giornalino l’ortografia non era un elemento secondario, dovendo scrivere ai corrispondenti era importante che il testo scritto fosse il più possibile corretto.
Non si doveva solo acquisire uno strumento ma c’era dietro una motivazione che dava senso anche al momento esercitativo. Separare i materiali da questo motivo significa snaturarne il significato.
Dopo aver svolto una serie di esercizi c’era una scheda di controllo che doveva essere corretta dall’insegnante. In base al risultato il bambino poteva procedere negli esercizi successivi (strettamente graduati!!!) oppure ripetere la serie.
Questo materiale può ancora avere una sua validità? Avrebbe senso rieditarlo, con eventuali aggiornamenti, per renderlo nuovamente disponibile?
Contemporaneamente sarebbe interessante, oltre che utile, elaborare materiali come la Biblioteca di lavoro o le Schede scolastiche cooperative (realizzate dagli alunni), indispensabili per portare avanti la ricerca d’ambiente e realizzare le conferenze, due ambiti su cui il Movimento ha ancora molto da dire. Che cosa ci offre già l’editoria MCE rispetto a questo? Che richieste possiamo fare agli esperti del MCE per produrre materiali adeguati e soprattutto “nuovi”? Quali collaborazioni esterne potrebbero essere utili?

Per mantenere la rotta occorre fare un passo alla volta.

È possibile, con uno sforzo comune dei gruppi di ricerca e dei gruppi territoriali, condividere i materiali prodotti relativamente alle tecniche in modo che si possano conoscere e confrontare e diventino parte dei materiali a disposizione degli iscritti (e non solo!) riattivando ciò che a suo tempo aveva fatto la Cooperativa per la Tipografia Scolastica? 
Ora abbiamo altri strumenti: spazi web su cui pubblicare, strumenti di comunicazione per diffondere. Serve però un progetto comune condiviso per mettere insieme le tante risorse già esistenti e crearne di nuove, validarle, classificarle, organizzarle in modo logico e facilmente fruibile per poi diffonderle.
Tempo fa si era tentata la creazione di una sezione didattica sul sito MCE ma la risposta dei gruppi era stata praticamente nulla quindi il progetto era stato dopo breve tempo abbandonato. È evidente che se non c’è interesse da parte di qualcuno e soprattutto se non c’è qualcuno che se ne occupa davvero i progetti nascono e muoiono. Speriamo che in questo caso le cose vadano diversamente.

Donatella Merlo, Sonia Sorgato
Gruppo Creazioni matematiche – settembre 2021

Riferimenti bibliografici su piano di lavoro e tecniche Freinet nell’articolo Sulle tecniche Freinet in questo stesso blog.
 

Nessun tag per questo articolo.

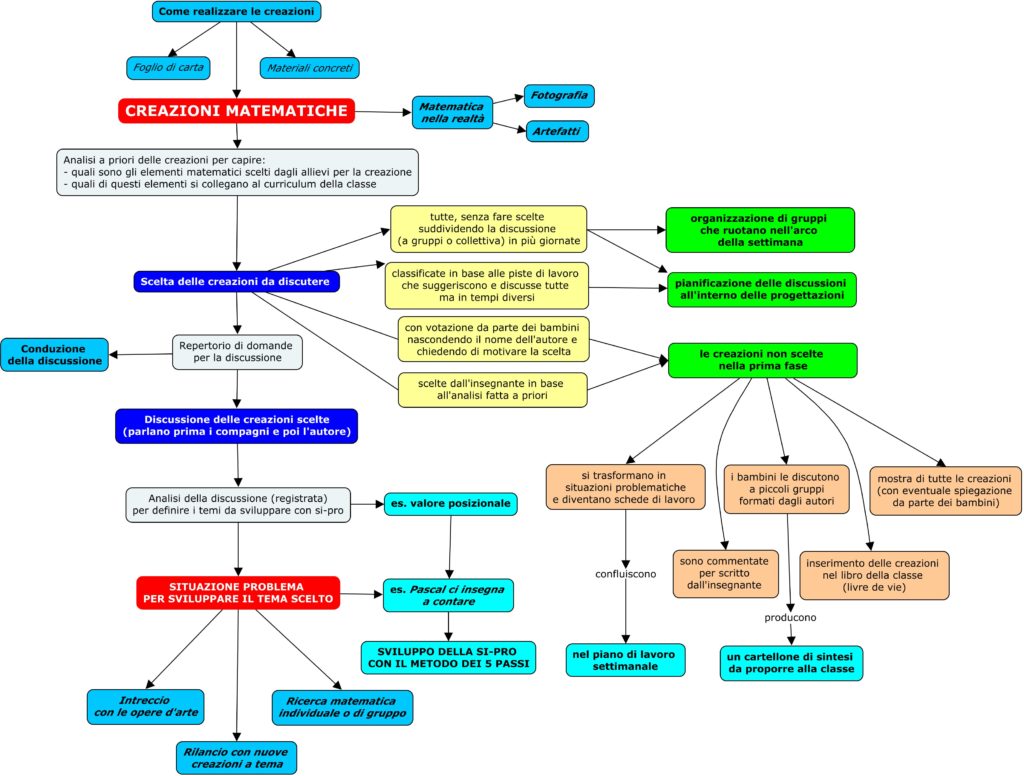
I gruppi di ricerca come il nostro si occupano di studiare e sperimentare, all’interno di un certo ambito di interesse, nel nostro caso la matematica, con lo scopo finale di diffondere pratiche didattiche coerenti con la pedagogia popolare di cui il Movimento è testimone. Per raggiungere questo obiettivo è anche importante produrre e diffondere materiali fruibili, internamente ed esternamente al Movimento stesso, per realizzare quel materialismo pedagogico che è un elemento fondamentale della pedagogia freinetiana.

Esistono molti gruppi nel Movimento che lavorano sulle tecniche Freinet all’interno di percorsi disciplinari frutto di ricerche di lungo periodo, costantemente in revisione e aggiornamento. Sono anche numerose le esperienze di sperimentazione delle tecniche documentate all’interno dei gruppi di ricerca: il testo libero nel gruppo di lingua, le creazioni matematiche, il giornale, il consiglio sono solo alcuni esempi. Una maggiore circolazione dei materiali prodotti e la ricerca di una validazione di questi materiali da parte di chi ha competenze, non solo pedagogiche ma anche disciplinari, dovrebbero essere intenti comuni a tutti i gruppi. 

Dal webinar del 25 settembre 2021 “Proviamo a cambiare didattica?”, a cui sono stati invitati esperti con competenze e punti di vista molto differenti, pensiamo di ricavare nuovi input per la ricerca del gruppo e nello stesso tempo raccogliere istanze dai partecipanti che ci aiutino a definire quali siano i tipi di materiali che potrebbero aiutare la diffusione delle nostre pratiche.

Nelle sperimentazioni di alcuni insegnanti del nostro gruppo si è già realizzata un’integrazione tra tecniche diverse (nel nostro caso tra creazioni, corrispondenza scolastica, piano di lavoro, brevetti….) secondo il principio freinetiano per cui le tecniche non debbono essere considerate le une isolate dalle altre ma pratiche che si realizzano compiutamente solo se inserite all’interno di un sistema. Questa idea delle tecniche come sistema è ciò che si dovrebbe cogliere da una lettura attenta non solo di ciò che ci ha lasciato in eredità Freinet ma anche dalla ricerca attuale che avviene nel nostro Movimento e anche all’estero, particolarmente in Francia. Queste esperienze rappresentano un’enorme ricchezza da cui è necessario partire: sono un patrimonio di ricerca che garantisce di tenere sempre presenti il senso, la coerenza e la correttezza dei materiali prodotti. La pedagogia freinetiana è di fatto una ricerca elaborata da chi la pratica quindi in continuo divenire in coerenza con i principi di fondo che l’hanno sempre ispirata.

Noi pensiamo che se isoliamo le singole tecniche dal sistema complessivo banalizziamo e strumentalizziamo ciò che invece anima ancora oggi la ricerca di molti di noi. Non possiamo prescindere dalle considerazioni di “cornice” che determinano l’ossatura del sistema: soltanto all’interno di una pedagogia cooperativa gli strumenti assumono un ruolo di emancipazione per i bambini e le bambine, emancipazione che è strettamente legata non solo alla pianificazione delle attività ma soprattutto ai processi di autovalutazione e autoregolazione che, inseriti all’interno di una pedagogia cooperativa, producono spazi di inclusione e differenziazione e animano la ricerca. Ha senso (ed è urgente), quindi, ragionare tutti insieme sulle tecniche e sulla loro attualizzazione condividendo le esperienze e facendo uno sforzo di elaborazione collettiva di linee guida per la costruzione di strumenti che possano supportare l’implementazione in classe delle tecniche. 

È necessario, parallelamente, un lavoro di ricerca storica sulle tecniche, non tanto perché dobbiamo adeguarci alle soluzioni – sicuramente, per certi aspetti, da ricontestualizzare – dei maestri e delle maestre che le usavano decine di anni fa (Lodi, Bigiaretti, Ciari, Fantini, Criscuolo per fare solo alcuni nomi) ma perché proprio a partire dal loro lavoro di ricerca, ampiamente documentato, possiamo trovarne gli elementi costitutivi e quindi capire come e dove apportare anche radicali modifiche per sviluppare le tecniche nelle nostre classi. Partire dalla nostra storia significa capire le ragioni profonde e ridare vita alle innovazioni portate dai maestri del passato che avevano l’intenzione viva di realizzare il dettato costituzionale rendendo la scuola strumento di emancipazione per tutti, esigenza reale o meglio “urgenza” anche per noi in questi anni. 

Per iniziare questo lavoro di approfondimento storico è utile coinvolgere le maestre e i maestri che hanno utilizzato le tecniche, analizzare i materiali che ne documentano il lavoro, presenti presso la sede di Roma, cercare e recuperare all’interno delle nostre scuole ciò che è rimasto di quel repertorio preziosissimo elaborato negli anni ’70 e ’80. In questo i maestri che non sono più in servizio potrebbero diventare un’utile risorsa.

È necessario inoltre rivolgere il nostro sguardo verso realtà al di fuori dell’Italia per confrontarci con materiali e strumenti che attualmente sono utilizzati (in Francia numerosi sono i materiali prodotti dall’ICEM, dal PIDAPI, dall’editore Odilon) e potrebbero quindi rappresentare una significativa fonte di ispirazione a cui attingere. 

La costruzione di materiali concreti, secondo noi, dovrebbe avvenire in seno ai gruppi di ricerca per garantire la correttezza rispetto all’impianto epistemologico di ogni disciplina. Avviata questa ricerca si devono individuare dei momenti di condivisione e di coordinamento, in particolare con gli esponenti dei gruppi dei 4 passi, in modo da favorire una reale integrazione tra il lavoro di ricerca disciplinare e le tecniche. Ad esempio il Gruppo lingua potrebbe occuparsi della realizzazione di schede di italiano coerenti con il lavoro di ricerca sulle concettualizzazioni di partenza dei bambini a cui viene proposto un approccio alla letto-scrittura basato sul metodo naturale e sulla scrittura spontanea, tenendo conto della diversità della situazione in cui si trovano ad agire gli insegnanti di oggi rispetto a quelli del passato. Infatti, per progettare attività di apprendimento della letto-scrittura in classi in cui il numero degli stranieri è in crescita, è necessario che gli insegnanti costruiscano nuove visioni e nuove competenze con il supporto di esperti che spieghino, ad esempio, come gestire l’abbinamento suono-segno in questa realtà mutata e composita. Le neuroscienze ci hanno aperto gli occhi su queste e altre difficoltà, anche per quanto riguarda la matematica, ma le nuove conoscenze raggiunte in questo campo non si traducono automaticamente in didattica, vanno prese per quello che valgono. Siamo noi gli specialisti della didattica, quindi tocca a noi insegnanti far buon uso delle conoscenze provenienti da ricerche scientifiche attuali per elaborare strategie didattiche che mettano sempre al centro il bambino. Le scoperte di una scienza che studia il funzionamento del cervello, prescindono dalle situazioni reali e soprattutto non tengono conto del fatto che i bambini, per apprendere, devono innanzitutto seguire dei percorsi di senso. Le competenze si costruiscono sempre a partire dai significati intuitivi, dalle conoscenze ingenue che vanno quindi prese come punto di partenza. Non dalla teoria.

Un gruppo MCE che focalizzi la sua ricerca sulle tecniche deve cominciare condividendo il senso da dare alle tecniche stesse nella scuola attuale elaborando innanzitutto dei principi comuni e ponendosi alcune domande di partenza.

Dal punto di vista della pedagogia:
Che cosa significa pedagogia cooperativa?
Che cosa significa pedagogia differenziata? Come si realizza concretamente la differenziazione? 
Il piano di lavoro, che si colloca all’interno di una pedagogia differenziata, come strumento per l’individualizzazione che ruolo assume nella nostra didattica quotidiana? 
Quali sono le relazioni del piano di lavoro con le altre tecniche (testo libero, creazioni matematiche, calcolo vivente, corrispondenza, conferenze, giornale di classe…)? Quali le scelte progettuali per integrarle? …

Dal punto di vista delle discipline:
Che cosa si insegna e come si insegna? 
Quali sono i modelli teorici rispetto alla disciplina che si insegna?
Quali sono i riferimenti attuali rispetto alla didattica di quella disciplina? …

Infine deve prendere in considerazione i rischi.

Tutte queste variabili condizionano i prodotti che si realizzano perché dipendono dal modo di insegnare di chi li propone e dai soggetti a cui li si propone. 

Avere riferimenti comuni non dà la garanzia che i materiali prodotti e condivisi vengano utilizzati da tutti nello stesso modo in quanto ognuno li adatterà al suo personale modo di fare didattica. Anche l’esercizio più banale, per restare nello spirito della pedagogica attiva, dovrebbe nascere da ciò che si è fatto prima in classe, dovrebbe essere un prodotto in cui i bambini si riconoscono perché richiama ciò che si è costruito tutti insieme, un prodotto della classe cooperativa che si innesta, senza soluzione di continuità, sul percorso progettato dall’insegnante e verificato nella relazione con gli alunni.

L’attenzione ai soggetti, cioè agli alunni, chiama in causa il concetto di “differenziazione” che, per realizzarsi, richiede azioni finalizzate a conoscere gli allievi uno per uno per individuare i loro punti di forza e di debolezza, per riconoscere gli inciampi che incontrano e studiare le modalità migliori per far loro superare questi inciampi. Non si realizza “solo” offrendo materiali a diversi livelli di difficoltà a libera scelta. Ogni bambino sa “cosa sa fare” e “cosa non sa fare”, se nella classe c’è una modalità di lavoro in cui la riflessione metacognitiva è parte della routine. C’è quindi una presa di coscienza continua delle proprie difficoltà e la consapevolezza che per superarle occorre lavorare in una certa direzione e soprattutto con qualche aiuto. È nel dialogo continuo che si realizza tra alunno e insegnante che avviene la differenziazione, non solo nella distribuzione di compiti o di schede a diverso livello di difficoltà. Anche per questo nell’organizzazione della classe cooperativa ci sono delle “istituzioni” che permettono di strutturare questo dialogo (cooperativa/consiglio, incarichi/mestieri…) nelle sue diverse dimensioni (tutoraggio, aiuto reciproco…).

Sonia Sorgato, Donatella Merlo
Gruppo nazionale Creazioni matematiche – settembre 2021

Riferimenti bibliografici
Boncourt, M. e Legay M. (2019). La pédagogie Freinet en élémentaire, ESF, Paris.
Bottero E. (2021), Pedagogia cooperativa. Le pratiche Freinet per la scuola di oggi, Roma, Armando.
Ciari B. (2012), Le nuove tecniche didattiche, Roma Edizioni dell’Asino.
Freinet C., La scuola moderna, Trieste, Asterios (collana MCE Narrare la scuola, in corso di pubblicazione).
Freinet, C. (1962). Les plans de travail,  Édition de l’École moderne française, Cannes. (disponibile all’indirizzo http://www.icem-pedagogie-freinet.org/node/18345, ultimo accesso 6 settembre 2021).
Freinet, C. (1969). Le mie tecniche, La Nuova Italia, Firenze.
Freinet, C. (2002). La scuola del fare, Junior, Bergamo.
Gruppo di ricerca MCE sulla valutazione (2020), Valutazione e metacognizione e i Brevetti, in Pedagogia dell’emancipazione e valutazione, eBook Collana RicercAzione, Edizioni MCE (acquistabile qui https://store.streetlib.com/it/gruppo-valutazione-mce/pedagogia-dellemancipazione-e-valutazione).
Laboratoire de recherche Coopérative de l’ICEM, Pédagogie Freinet, Dictionnaire de la pédagogie Freinet, Paris, ESF, 2018.
Le Bohec, P. (2019). Il testo libero di matematica, eBook Collana RicercAzione, Edizioni MCE (acquistabile qui https://store.streetlib.com/it/paul-le-bohec/il-testo-libero-di-matematica).
Sorgato S., Valentini E. (2020), Faccio i complimenti a me stessa perché ho lavorato bene, in Cooperazione educativa giugno 2020. Trento: Erickson. 
Tamagnini G. (1965), Didattica cooperativa, Le tecniche Freinet in Italia, Frontale, Movimento di Cooperazione Educativa, (nuova edizione ridotta, Junior, 2002).
Sulle tecniche Freinet articoli e video sono disponibili qui: https://www.enricobottero.com/pedagogia-freinet
Per reperire materiali utili consultare anche: https://www.icem-pedagogie-freinet.org/accueil-outils-et-publications

Nessun tag per questo articolo.

Rileggendo l’articolo di Le Bohec sulle creazioni matematiche scritto per Cooperazione Educativa n. 3/2000 ho trovato nuovi spunti sia di riflessione che di lavoro per il nostro gruppo di ricerca.

Vorrei mettere in evidenza un aspetto significativo di questa ricerca, il fatto che durante le discussioni che conduciamo sulle creazioni spesso si hanno evidenze di una presa di coscienza da parte dei bambini di concetti fondamentali della matematica. Quando i compagni interpretano una creazione mettono in gioco tante “intelligenze” diverse, tanti modi di guardare diversi… Chi ne trae beneficio, dice Le Bohec, sono soprattutto gli autori, costretti, dagli interventi dei compagni, a mettere in discussione le loro rappresentazioni mentali. Questo mi sembra un aspetto caratteristico delle creazioni, il fatto che obbligano la mente a continue ristrutturazioni delle reti di significati che i bambini via via si costruiscono. E sono le sorprese, le visioni inaspettate che aiutano a procedere. Aiutato dai compagni ogni bambino inizia a vedere la propria creazione dall’esterno e quindi riesce anche a valutarla, a criticarla se necessario, individuando degli errori, a cercare poi di migliorarla. Si appropria quindi del sapere matematico e ci fa vedere che se ne è appropriato con i fatti e con le parole.

Un altro elemento, più pratico, è il fatto che Le Bohec “estraesse” dalle creazioni dei bambini solo quelle parti che voleva mettere in discussione nella classe. Era ancora più selettivo di noi che ci limitiamo a scegliere fra tutte le creazioni quelle che ci sembrano più coerenti con il percorso che immaginiamo possa condurre verso la costruzione di nuovi saperi, grazie alla nostra esperienza come insegnanti, da un lato, e alla conoscenza della matematica, dall’altro.

Le Bohec scrive: “…si cercava di sviluppare una produzione, la si riprendeva, la si allargava. Si aiutava a volte l’autore a sviluppare la sua idea fino in fondo. Si notava un grande piacere nello sperimentare, ma anche nel copiare, o nel sorprendere, o nell’esprimere, attraverso l’espediente della matematica, un problema personale.”

Questi aspetti emozionali e affettivi legati alle creazioni li abbiamo sperimentati anche noi e sono veramente fondamentali; lo diventano ancor più se questa pratica diventa parte delle routine della classe perché inserita nel piano di lavoro. Scrive Le Bohec: “Gli insegnanti che, per prudenza, non hanno osato lavorare in questo modo che una volta sola alla settimana, non hanno visto le cose svilupparsi come l’avrebbero desiderato.”

Un’ultima riflessione riguarda il ruolo dell’insegnante nella discussione: “…egli deve guardarsi dall’intervenire troppo presto in quanto, perché ci sia comprensione, occorre che ci sia stato innanzitutto un lavoro di ricerca, un’apertura dell’intelligenza verso una domanda.” Ritornando a quanto si diceva prima sul fatto che le creazioni devono condurre a una trasformazione delle rappresentazioni mentali Le Bohec afferma che “occorre esser messi davanti a delle affermazioni che sorprendano, che pongano problemi.”

Altrimenti quel processo di ristrutturazione necessario per imparare non può partire. Questo è tutto.

Nessun tag per questo articolo.