Paola Spolaor, classe quinta, Spinea (VE)

















Descrizione delle creazioni di coppia o piccolo gruppo
Auto
Una creazione geometrica per me significa una costruzione nuova o fatta a modo mio che contenga la geometria.
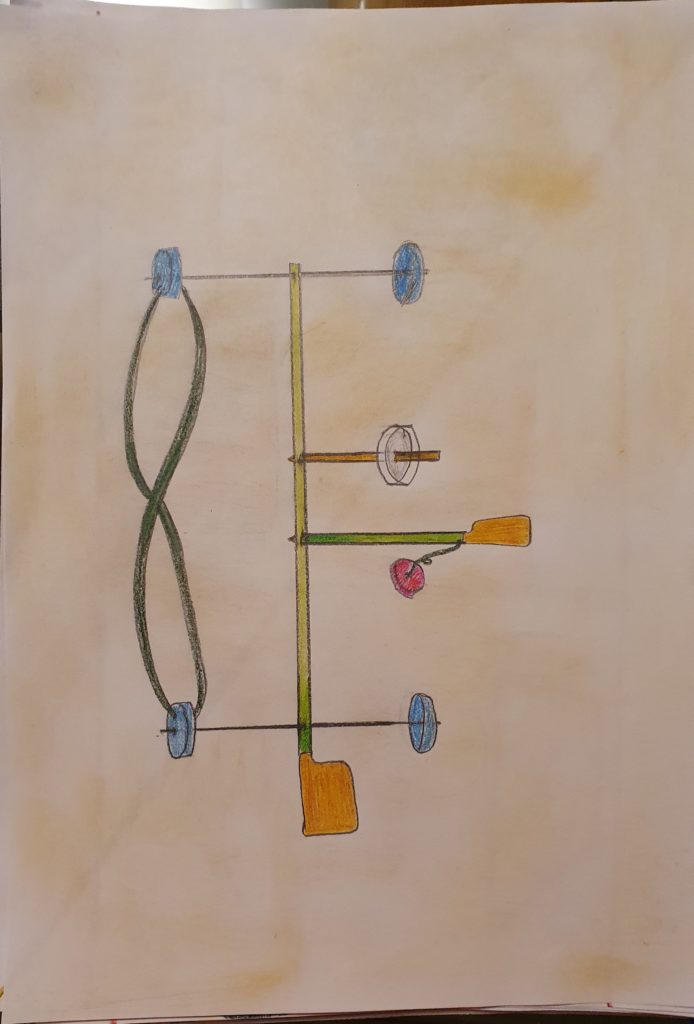
La mia creazione geometrica rappresenta un’auto: la sua base è una cannuccia che è attraversata circa sulle estremità da due lunghi stuzzicadenti che hanno due tappi infilzati sulla fine. Le 4 “ruote” hanno dei buchi interni rispetto all’auto. Nei buchi sono infilati dei fili di lana che collegano la ruota destra anteriore e posteriore e viceversa, formando un quadrato. Ci sono anche altri due stecchini, infilati perpendicolarmente alla cannuccia e agli altri due, che servono come decorazione: uno dei due ha attaccato un tappo e funge da finto volante, mentre l’altro ha attaccato un filo che tiene legato un tappo. (Tommaso)
Forme geometriche
Per me una creazione geometrica è un insieme di figure.
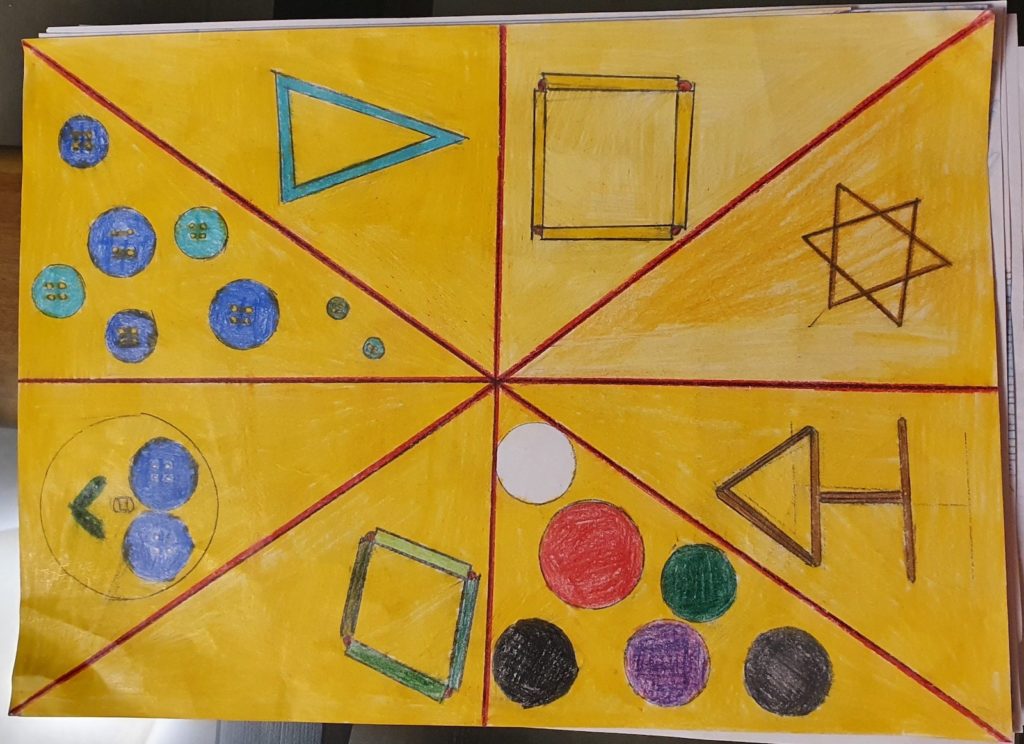
Noi abbiamo messo dei fili di lana in verticale, in orizzontale, e due oblique opposte, e ci sono venuti otto triangoli. In un triangolo abbiamo messo sei tappi, in un altro un albero fatto con gli stuzzichini, in un altro la stella di David, in un altro ancora un quadrato fatto con una cannuccia, poi in un altro triangolo un triangolo isoscele, e un altro otto bottoni, in un altro ancora un cerchio con della lana, due bottoni e due pezzetti di cannuccia, che formano una faccina, e infine un rombo con della lana e delle cannucce.
La nostra creazione rappresenta otto triangoli e dentro ogni triangolo ci sono figure geometriche diverse. La nostra creazione significa che ogni figura geometrica si può raffigurare con ogni materiale. (Giorgia)
Per me creazione geometrica vuol dire creare una figura con diverse regole.
Ho creato su un piano delle strisce 2 oblique, 1 verticale e 1 orizzontale bianche, e le ho attaccate con lo scotch. Si sono formati dei triangoli. In ogni triangolo ho disegnato con materiali diversi figure geometriche. In un triangolo ho disegnato un albero con gli stecchini, poi in un altro ho disegnato / creato con le cannucce un quadrato e poi un triangolo e un parallelogramma.Con i tappi e i bottoni gli ho sparsi. Infine con uno spago ho disegnato un cerchio e dentro 2 bottoni gli occhi, con un piccolo pezzo di cannuccia il naso e con uno più grande la bocca. Ho creato un mix di figure geometriche creandole con ogni materiale. (Francesca)
Per me raffigura una specie di tangram con la maggior parte delle figure geometriche. (Fabio)
Per me una creazione geometrica vuol dire una figura precisa ma anche inventata perchè secondo me le figure vanno inventate ma con le sue proprietà sempre inventate.
La nostra creazione descrive 4 cerchi, 2 trapezi, 4 triangoli, e 2 rettangoli messi nella nostra maniera, fatti con la fantasia seguendo le regole. La nostra creazione rappresenta tutte le forme geometriche facili, la nostra fantasia ci ha aiutato a farle, mettendo insieme le nostre idee di gruppo. (Azzurra)
Girandola o giostra
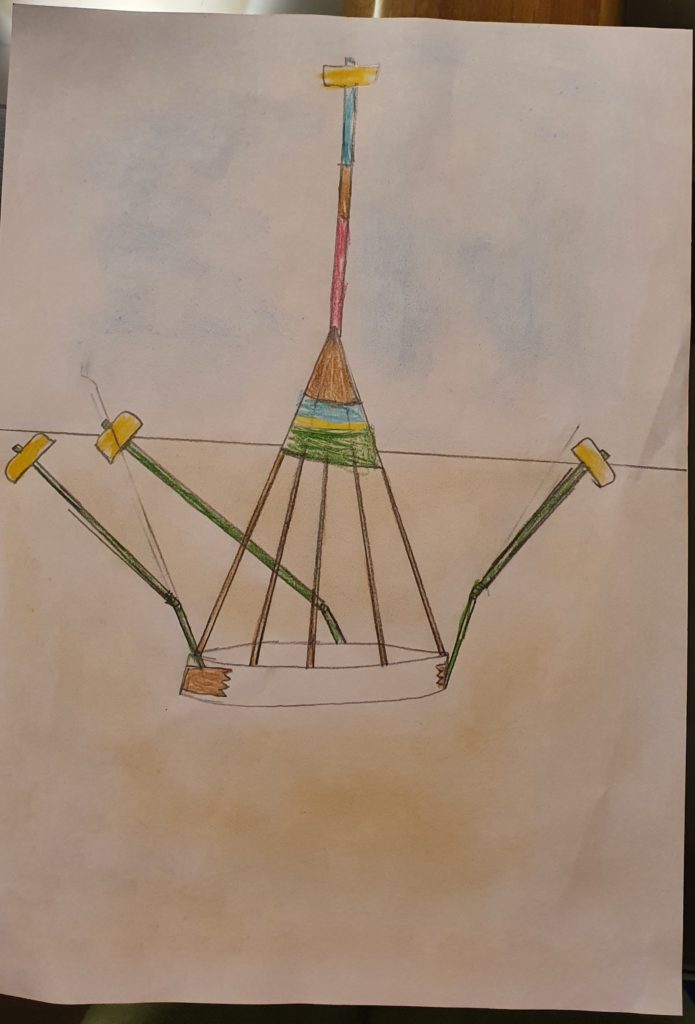
La costruzione che abbiamo ideato l’abbiamo chiamata Girandola. Per crearla abbiamo utilizzato come base un tappo abbastanza alto e largo. Al centro del tappo abbiamo messo uno stuzzicadente per spiedino mentre ai lati ne abbiamo messi otto che si incontravano sulla punta dello stuzzicadente al centro, visto che erano laschi gli abbiamo legati con dello scotch. In punta abbiamo messo una cannuccia con in cima un tappo di una bottiglia. Abbiamo fatto la stessa cosa ai lati del tappo (base) attaccando le cannucce con dello scotch nel contorno di esso. Sotto lo scotch che si trovava in punta abbiamo messo uno strato di nastro verde per dare un po’ di colore alla creazione, sotto del filo verde abbiamo messo del nastro arcobaleno. La nostra idea era quella di fare una figura solida invece che piana basandoci su un cono. Per vederla bene per ricordarla nel tempo. Ci hanno ispirato le giostre del luna park che girano con le seggiole sostenute su una struttura al centro. (Giacomo)
Per me creazione geometrica significa costruire con pezzi geometrici.
La creazione che ho fatto con Bianca e Giacomo, a come base un tappo di nutella, abbiamo fatto l’altezza con una stecca, intorno abbiamo messo tante stecche, e li abbiamo legati insieme con lo scotch, il cono che è venuto fuori lo abbiamo decorato in cima con la lana e una cannuccia con un tappo sopra. Intorno al tappo che fa da base, abbiamo messo 3 cannucce con in cima un tappo. Per me la creazione che abbiamo creato sembra un giostra del luna park, in senso geometrico sembra un cono. (Alex)
Per me creazione geometrica è una creazione fatta con materiali geometrici. Una creazione si fa per modellare, montare e costruire con i materiali che si hanno usando le regole della geometria.
Abbiamo preso un grande tappo e al centro l’abbiamo bucato e infilzato con un bastoncino. Quel bastoncino è diventato l’altezza, da là abbiamo attaccato altri bastoncini fino a farli arrivare alla punta dell’altezza. Dopo aver fatto questo abbiamo attaccato lo scotch e così è venuto fuori un cono. L’abbiamo rivestito solo nella punta con della lana e ai lati esterni del tappo abbiamo attaccato 3 cannucce. Abbiamo bucato 3 tappi e li abbiamo infilati nelle cannucce attraverso il buco. Dopo aver infilzato un’altra cannuccia nell’incrocio dei bastoncini cioè nella punta del cono, abbiamo bucato un altro tappo e lo abbiamo infilzato nella cannuccia formando così una giostra. (Bianca)
Pesce
Per me la parola creazione geometrica significa mettere insieme varie figure geometriche senza seguire istruzioni.
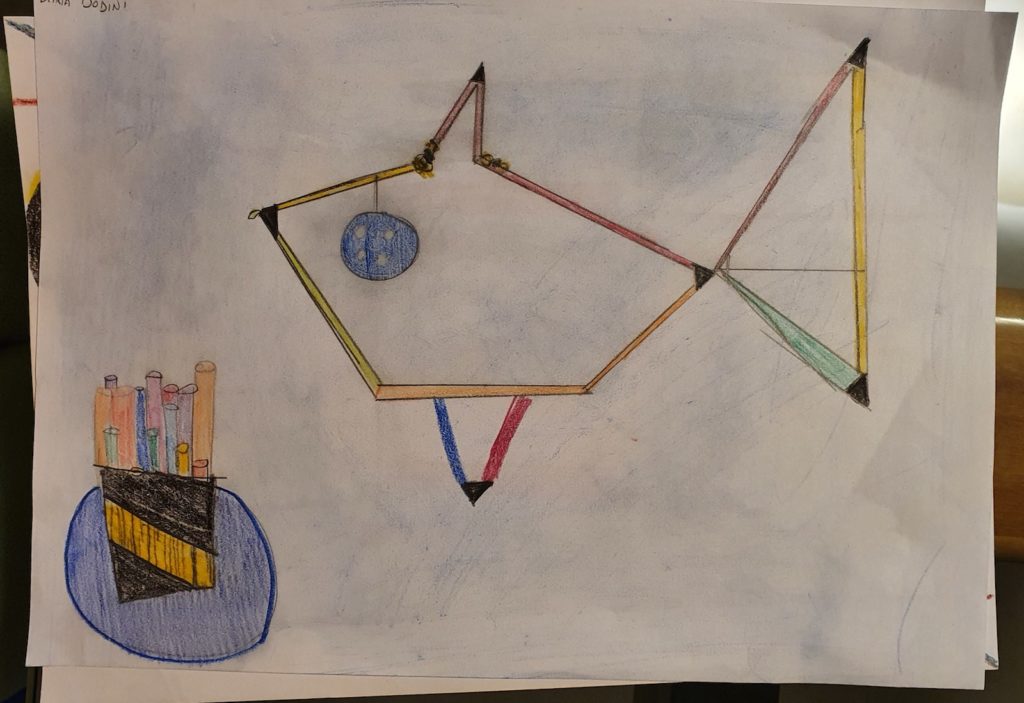
Io, Biagio e Anita abbiamo costruito un pesce. Come costruire il pesce: prendere una quindicina di cannucce e unirle con dello scotch. Questo diventa l’appoggio. Prendere quattro cannucce e formare un rombo. Prendere altre tre cannucce e incastrarle fino a formare un triangolo equilatero. Poi con uno stuzzicadente unire il triangolo con il rombo, adesso si è formata la struttura. Prendere due cannucce e trasformare in triangoli, poi con lo scotch attaccarle alla struttura del pesce. Prendere un bottone e del filo, far passare il filo attraverso il bottone, a questo punto legare il filo con il bottone sul lato del rombo. Questa è la creazione del pesce. La nostra creazione rappresenta un pesce e significa la vita in mezzo al mare. (Marco)
Per me una creazione geometrica è qualcosa di modificato da una figura già nota. Per costruire la nostra creazione geometrica bisogna fare un rombo con le cannucce. A una estremità del rombo abbiamo attaccato con lo scotch un triangolo fatto di cannucce. Ai vertici della diagonale minore abbiamo attaccato due piccoli angoli fatti di cannucce. È venuto un pesce che per me significa la vita nel mare. (Biagio)
Stella di David
Per me, la creazione geometrica è l’immaginazione della mente che genera il suo pensiero.
Per prima cosa abbiamo fatto una croce e una x con del filo, poi con dei tappi abbiamo fatto dei cerchi, abbiamo tagliato delle cannucce in quattro e abbiamo infilato dentro del filo creando un rombo, abbiamo costruito la stella di David con degli stuzzicadenti, abbiamo poi creato un viso con del filo, usato dei bottoni per gli occhi, delle cannucce per la bocca e il naso. A fianco abbiamo creato un quadrato con delle cannucce e con dei bottoni un cielo stellato. Io da questo lavoro, mi aspettavo esattamente quello che abbiamo costruito, un mondo di figure geometriche dove ognuno può immaginare quello che desidera. (Sebastiano)
Per iniziare abbiamo fatto un cerchio. Abbiamo fatto una linea retta nel mezzo del cerchio e continuato come quando fare il triangolo equilatero ma abbiamo fatto un altro arco dalla parte opposta dell’altro arco. Poi abbiamo fatto i 2 triangoli equilateri con sopra i fili di lana, abbiamo sparso un pò di brillantini e così si è creata la stella a 6 punte. (Dario)
Per me creare qualcosa vuol dire usare la propria fantasia per costruire un oggetto unico, ma significa anche costruire qualcosa (esempio: un triangolo) sapendo già la tecnica.
Io ho creato la stella di David:
-per prima cosa ho creato un cerchio a mano e ho tracciato il diametro;
-poi, sempre a mano, ho tracciato due semicerchi all’estremità del diametro;
-ho tracciato delle linee che collegano fra loro i punti di intersezione formati dai due semicerchi;
-infine ho usato lo spago per costruire i due triangoli attaccando le estremità (dello spago che forma i triangoli) sui punti di intersezione sulle estremità del diametro;
-per decorare ho sparso vari tipi di bottoni all’interno della stella.
Devo dire che per me la creazione che ho fatto è stata la meno bella, per di più non amo i lavoretti. Forse dovevamo metterci più creatività ma in sè è bellina. Per me questa creazione spiega che anche seguendo un metodo fai una creazione tua o non tua. (Alessandro)
Fiore
La creazione che ho formato con il mio gruppo è stata realizzata con dei tappi bianchi come “prato”(solo per 2 strati), filo di lana tutto compatto per formare il “gambo del fiore” che lo abbiamo messo in mezzo ai tappi, sempre con del filo di lana abbiamo creato il contorno del “fiore” che al suo interno ci abbiamo messo dei tappi di quasi tutti i colori, e un tappo di un barattolo al centro del “fiore” cioè un cerchio. Poi abbiamo messo all’estrema sinistra in alto un quadrato giallo con: del filo di lana tutto colorato nei margini e dell’altro filo di lana rosso in centro per creare il “sole”, vicino al “sole” abbiamo messo un filo di lana bianco per creare le “nuvole” e con delle cannucce azzurre abbiamo creato il “cielo”. (Roberto)
La creazione geometrica che abbiamo fatto rappresenta un fiore creato con: tappi, bottoni, fili di lana, un quadrato di colore giallo come sole e cannucce come cielo. Per crearlo basta creare un cerchio con tappi e bottoni attaccandoli con lo scotch. In centro si mette un tappo più grande tipo quello della marmellata, sopra quel tappo si appoggia una rosa fatta con la lana rossa. Per crearla basta avvolgere la lana rossa intorno a un bottone e dopo metterla sopra il tappo della marmellata, lo stesso procedimento per i petali. Per fare il gambo basta prendere un filo di lana verde e attorcigliarlo su se stesso e posizionarlo sotto il fiore. Poi abbiamo fatto il prato incollando un pò di tappi. Per fare il cielo bisogna prendere lana bianca per le nuvole e cannucce azzurre per il cielo poi tutto questo si attacca con lo scotch. Per fare il sole abbiamo preso un quadrato giallo avvolgendolo nella lana colorata e poi abbiamo messo al centro un gomitolo di lana rossa. (Elisa)
Cosa vedi di geometria nella creazione…
FIORE Gruppo: Roberto, Thomas, Elisa

An: vedo tanti cerchi,linee curve e rette nel cielo,un quadrato giallo che fa il sole.
Tomm.Si linee curve sullle nuvole…
Alex.Il gambo del fiore è un rettangolo
Giorg. La terra è formata da tanti tappi che formano 2 trapezi rettangoli..
Nic.il piano di appoggio della creazione è un rettangolo..
Bianc. Sui tappi ci sono delle stelle formate da triangoli piccoli.
Giaco: io vedo una grande circonferenza che contiene tanti cerchi,
Marc. Nella circonferenza ci sono tanti cerchi,cioè tanti tappi di tanti colori,se unisco i tappi rossi formiamo un triangolo . Se unisco un tappo,che è come un punto o un vertice,con un altro tappo disegnando un segmento, formiamo triangoli interni alla circonferenza
Azzurra: O un rombo,con i tappi arancioni..
Biagio:O un triangolo isoscele,mi pare che due lati sono uguali..
Vitt. Vedo anche nel cielo una circonferenza di lana..
Alex.Ma il cerchio e la circonferenza sono la stessa cosa?
Fabio. No! Il cerchio è la forma con l’interno…lo spazio dentro..La circonferenza è solo il bordo..
Alessandro. Cioè il perimetro..
Franc.Vedo un triangolo,ci sono circonferenze sovrapposte crescenti anche al centro del fiore…dalla più piccola alla più grande.
Giorgia.Le circonferenze esterne al cerchio grande possiamo unirle con dei segmenti e formare un triangolo isoscele forse?!
Giacomo.Dobbiamo verificarlo perchè i due tappi che formano la base non sono paralleli tra loro e se prolunghiamo l’altro tappo facendo cadere a picco sulla base ,non cade a metà esattamente..
Noemy.Vedo anche un trapezio unendo i tappi colorati..
Dario. Azzurra diceva un rombo per me è un parallelogramma,non mi sembra che ha i lati uguali…
Emiliano. Anche i bottoni hanno 4 fori paralleli e uniti formano un quadrato..
Azzurra. Nel cielo vedo triangoli e nel terreno dei rettangoli..
Alek. Vedo linee perpendicolari
Dario. Anche un pentagono con i 5 punti uniti.
Giorgia. Sul sole c’è un quadrato con sopra un cerchio ,con le parti non occupate dal cerchio posso formare un altro quadrato?!
Marco. O un rettangolo?!
Ins. Bisognerebbe provare a scomporre e ricomporre..
Giacomo. Il gambo è vero.. è perpendicolare al fiore e al terreno…cioè forma 2 angoli retti.
Ora parla uno dei componenti del gruppo:
Roberto: Non credevo di vedere tutte queste figure geom.L’abbiamo fatto a caso. Per noi era un fiore fatto di cerchi..
LA GIOSTRA Gruppo: Alex, Bianca, Giacomo

Alessandro: Il coperchio che sta alla base può essere un cerchio,ma per me è un cilindro senza una faccia…concavo..
Sebastiano.Lo scotch che unisce le cannucce è un parallelogramma.
Azzurra. Gli stecchini formano tanti triangoli uniti al centro in alto in un unico punto.
Roberto: la punta e le due cannucce formano un triangolo…isoscele se le cannucce sono uguali.
Nicoleta:All’interno del cono c’è un volume …è una figura 3D…tridimensionale c’è spazio dentro, ed è formata da tanti triangoli piani.
Elisa: Lo stecchino centrale al cono è una linea retta che cade al centro del coperchio.
Ins: Osservate bene il coperchio che sta alla base,e gli stecchini che si appoggiano all’interno…
Anita: sotto al coperchio c’è un cerchio …sono sovrapposti
Roberto. Se immagino di unire tutti i punti degli stecchini dentro al coperchio,tranne quello al centro, ottengo un ottagono dentro al cerchio.
Marco . La giostra non è un cono…è una piramide!!…a base ottagonale..mi sembra che si dice..
Ins. Lo stecchino centrale a cosa corrisponde per quella piramide …
Francesca. cade sul punto mercio del cerchio..
Ins. Ma che cos’è il punto medio per il cerchio?
Franc.E’ il centro del cerchio..dove è fissato lo stecchino centrale…e cade perpendicolare al piano di appoggio,cioè al coperchio ,anche la cannuccia fissata sopra alla piramide è perpendicolare..
Tommaso. Sì è l’altezza della piramide,lo stecchino centrale..
Parla un componente del gruppo:
Bianca:Anche io ho visto tutte queste cose ora..e le cannucce piegate le abbiamo piegate per fare degli angoli ottusi
Alex. Prima doveva essere un cono…poi è diventata una giostra
Giacomo:la giostra delle catenelle
Ins. I tappi bianchi inseriti alle estremità delle cannucce ,si muovono sono fissi?
Giacomo. I tappi bianchi scorrono lungo le cannucce e ruotano intorno al punto di intersezione,in questo caso al centro con la cannuccia inserita
Alex la base che sta sotto al coperchio bianco dovrebbe ruotare su se stessa per far muovere la struttura della giostra intorno.Avevamo preso lo stecchino centrale che fa da asse del cerchio e fa da perno nel ruotare intorno a se stesso.
Tema scelto: quadrato circoscritto e inscritto in una circonferenza
Conversazione su: Cerca di spiegare le proprietà della circonferenza e del quadrato, punti in comune tra le due figure e non.
Conversazione e uso degli strumenti (compasso, squadra..) e su Geogebra successivamente, per risolvere il problema: come faccio a costruire un quadrato e, successivamente, un quadrato circoscritto e inscritto in una circonferenza .
Conversazione, riflessione collettiva, approfondimento sull’utilizzo dei concetti geometrici conosciuti e utilizzati nella costruzione: perpendicolarità., parallelismo, simmetria, asse del segmento, per due punti passa una sola retta, la retta è formata da infiniti punti… punto medio di un segmento…
Costruzione ragionata e uso consapevole dei concetti sopra esposti per la costruzione di un quadrato inscritto e poi circoscritto ad una circonferenza.
16 marzo 2021
18 Marzo 2021
Proviamo a costruire altri poligoni regolari…: conversazione su un tutorial per la costruzione di un pentagono inscritto e tentativo di comprendere i concetti e le regole conosciute sulla scomposizione di un poligono in triangoli congruenti, le proprietà dei triangoli, la somma degli angoli interni di un triangolo…
7 aprile 2021
Non comprensione del tutorial e avvio conversazione per trovare un modo per costruire il pentagono con le conoscenze possedute: la somma degli angoli interni di un triangolo è di 180°, il pentagono è formato da 5 triangoli isosceli congruenti, l’angolo al vertice è di 72°…
Revisione e consolidamento delle proprietà e concetti geometrici utilizzati per la costruzione del quadrato inscritto e circoscritto ad una circonferenza: realizzazione su GeoGebra su foglio bianco (non quadrettato).
13 aprile 2021
Libro Geogebra: Quadrato, cerchio e poligoni iscritti e circoscritti
19 maggio 2021
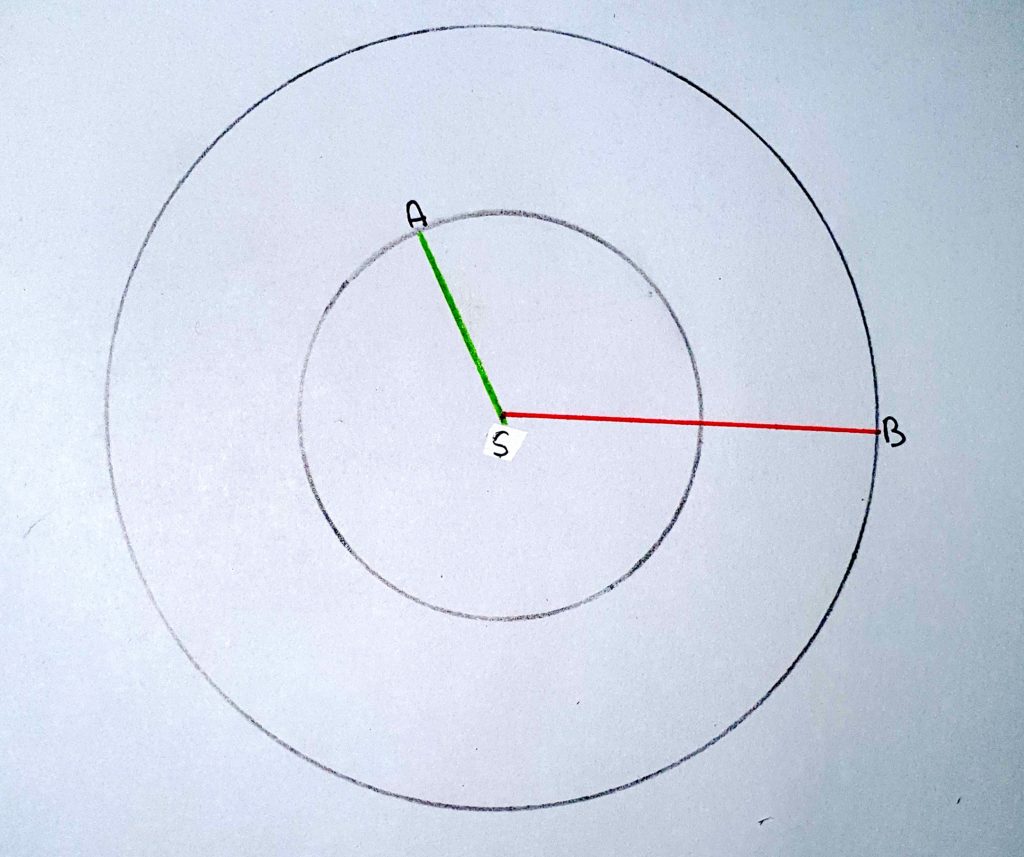
SITUAZIONE PROBLEMA: La distanza casa-scuola
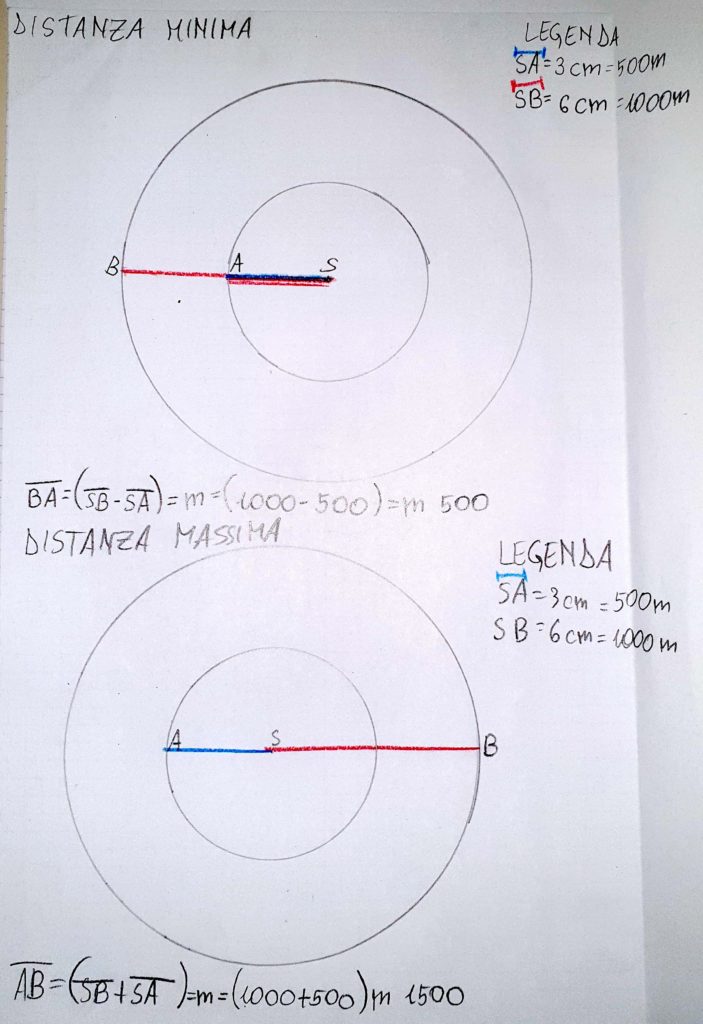
Ultima riflessione sul lavoro Percorso scuola-casa.
Dopo aver realizzato in modo operativo il percorso in atrio e realizzato il modellino in cartoncino per rappresentare le varie posizioni sul piano dei percorsi casa-scuola di A e B, in un incontro successivo abbiamo ripreso l’argomento ed evidenziato le seguenti conclusioni:
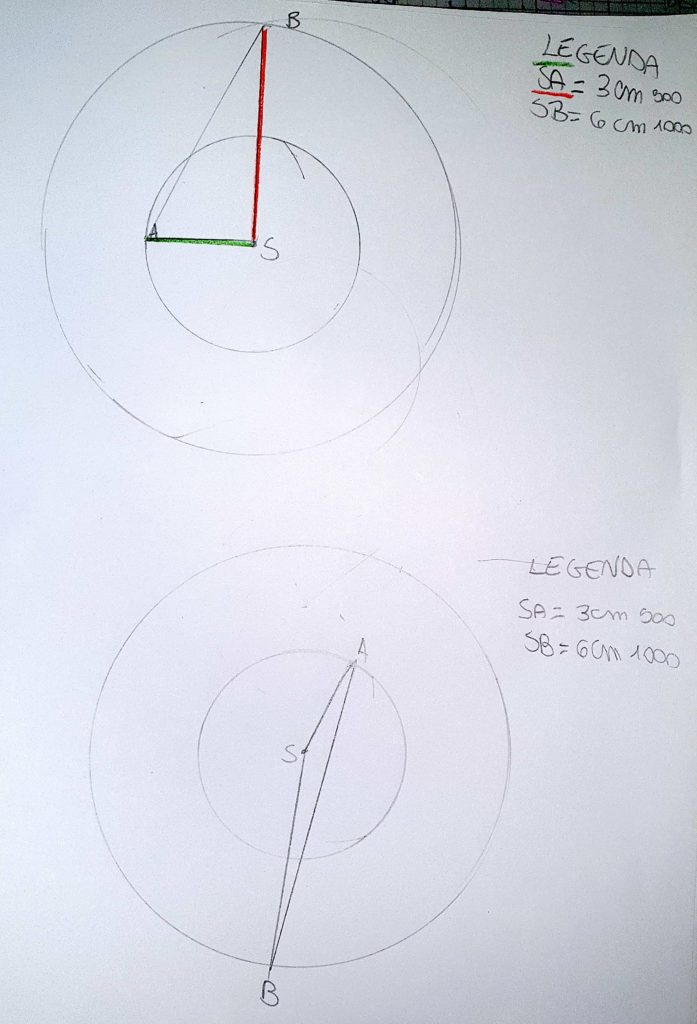
Tutti i ragazzi hanno rappresentato sul quaderno, su foglio bianco, le tre posizioni (minima, massima e media**) e poi hanno avviato la discussione sulle altre possibili posizioni delle case, fermo restando che il centro era la scuola.
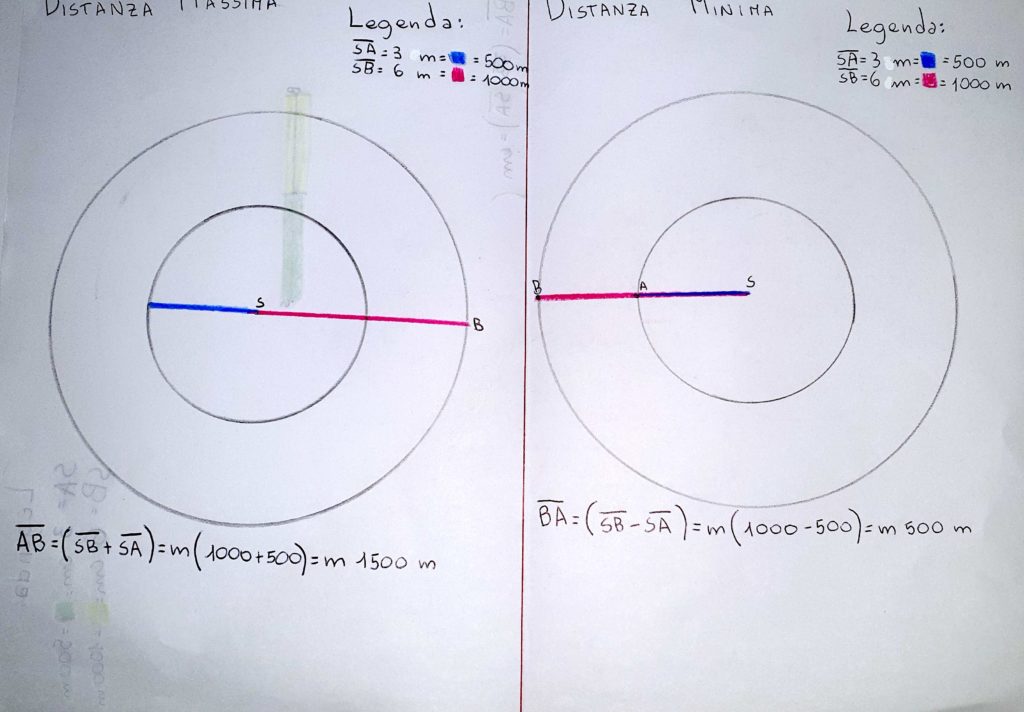
Alessandro. Le posizioni delle case possono essere tante a seconda della rotazione che noi facciamo della casa di A o di B…Certo la massima è 1500 m. dove le case sono una opposta all’altra rispetto alla scuola al centro…e si forma dalla rotazione di 180°. Se facciamo ruotare una casa di 180° ,si trovano nella stessa retta e dalla stessa parte rispetto alla scuola e abbiamo la distanza minima, cioè 500 m.
Giacomo: Ce ne sono infinite posizioni… Almeno 360° se spostiamo una casa, una per ogni angolo di rotazione….
Vittoria: Ma se una circonferenza è formata da infiniti punti, allora ci sono infinite posizioni, una per ogni punto..
Alex: Anche io dico che ci sono infinite posizioni come ha detto V.
Nicoletta: Se guardiamo i gradi degli angoli allora sono 360 posizioni per una casa e 360 se faccio ruotare l’altra casa, cioè almeno 720 posizioni..
Marco: Ma ci sono posizioni che si ripetono o sono speculari.
Ins. Ci sono posizioni simmetriche che hanno stesse distanze.
Giacomo: ma tra un grado e l’altro ci sono decimi, centesimi …di grado quindi alla fine sono infinite posizioni… Sono come le lancette dell’orologio…i minuti è la distanza da SB e le ore la distanza SA.
Ins. Alessandro ha calcolato la distanza massima e minima dei due percorsi, quando le due case sono sulla stessa retta (opposte rispetto al centro o dallo stesso lato) .
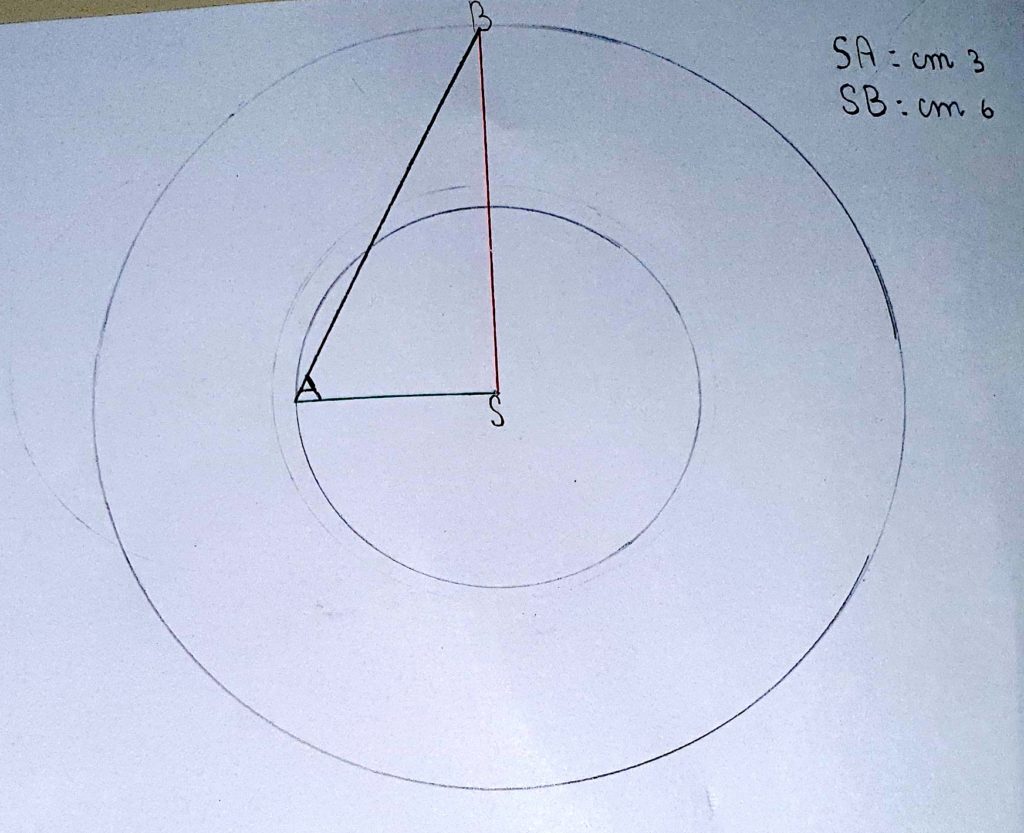
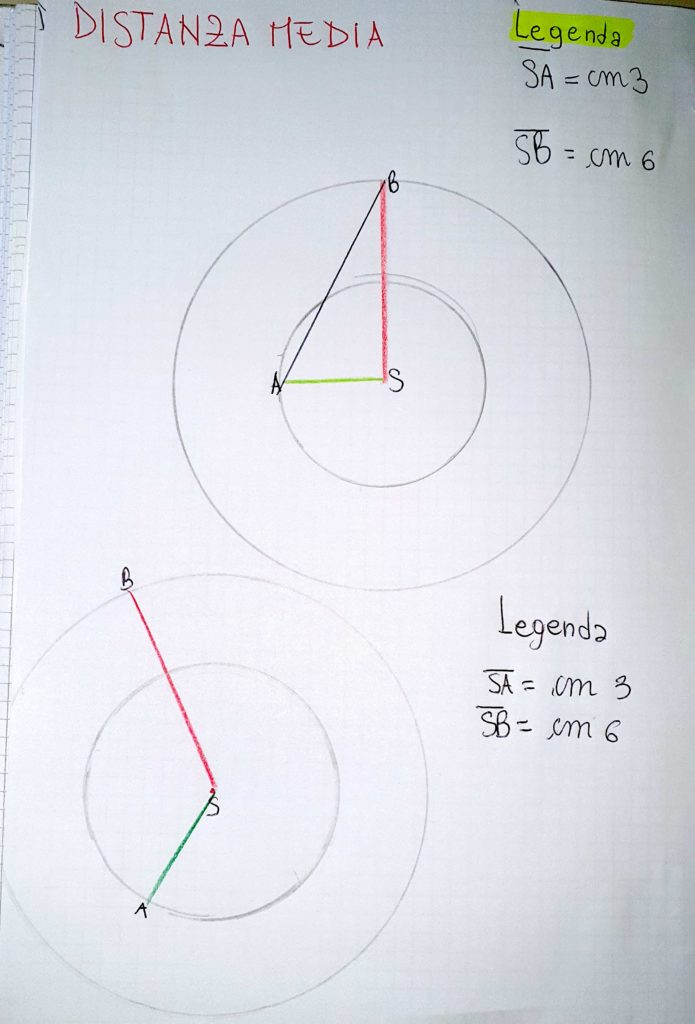
Come possiamo trovare la distanza nella posizione intermedia, quando le due case formano un angolo retto?
Alessandro: In questo caso basta unire B con A .
Marco: Viene fuori un triangolo..
Alex: Un triangolo retto.
Nicoletta: un triangolo rettangolo.. Conosciamo le misure dei lati che formano il triangolo…Forse ci sarà un modo per trovare l’altro lato.
Alessandro: l’ipotenusa. Io so che mia sorella lo sa calcolare , alle medie..
Ins. Sì è possibile calcolare la misura dell’ipotenusa, grazie al teorema di Pitagora che avremo potuto scoprire anche noi se avessimo avuto un po’ di più tempo….Ma che certamente scoprirete alle medie.
**L’uso del termine ” distanza media” andrebbe evitato perché può veicolare la falsa idea che le situazioni possibili siano solo 3 mentre i bambini hanno ben chiaro che le distanze “medie” sono… infinite. In questi casi è importante che l’insegnante intervenga subito per creare un conflitto cognitivo: esiste una distanza media? I bambini in realtà chiamano “distanze medie” tutte quelle che stanno fra la minima e la massima con un’attenzione particolare a quella dove l’angolo è di 90° e quindi li porterebbe, come dice l’insegnante alla fine, verso il teorema di Pitagora essendo una situazione particolare. (D.M.)
Libro Geogebra: La distanza da casa a scuola
26 maggio 2021
La Geometria scoperta e ritrovata nell’arte contemporanea


L’ins. mostra alla LIM varie opere d’arte di Kandinskij e di V. Vasarely
La classe ,dopo averle analizzate , sceglie un’opera per ogni artista che più si integra con il lavoro svolto nelle creazioni geometriche.
Viene scelta l’opera “Quadri” di Kandinskij e “Vega 200” di Vasarely
Si inizia ad osservare attentamente l’opera di Kandinskij..e si avvia la conversazione sulle impressioni, emozioni rilevate.
Azzurra: ci sono 12 quadrati con dei cerchi inscritti, hanno colori diversi, dimensioni diverse, i cerchi,
Tommaso: Mi è venuta in mente la cartina fisica che è dentro ad una griglia, reticolato e i colori indicano le profondità o le altitudini…
Alessandro: Sembrano dei” buchi neri “(abbiamo appena approfondito l’universo e il sistema solare)colorati, allegri , ma mi ricorda un quadro in cui in ogni quadrato c’era il volto di una donna, della Pop Art…non mi ricordo l’artista
Azzurra:Hanno dimensioni differenti ,la stessa immagine del quadrato con i cerchi inscritti riprodotta 12 volte ma con colori deversi, il colore ti dà l’idea di profondità come fossero in 3D.
Francesca: Tanti cerchi sovrapposti non perfetti,irregolari ,ma con il centro in comune.
Marco: sono cerchi concentrici







Anita: sembrano cellule che formano un tessuto…
Noemy: Si possono immaginare elementi naturali che si uniscono per formare organismi.
Si passa poi all’analisi del quadro “Vega200 “di Vasarely.
Rob. E’ come una grande palla ,racchiusa nel vuoto..
Daria. Ci sono dei quadri con dei cerchi inscrittti.
Francesca: E’ un quadrato circoscritto ad una mezza sfera.Vuole dimostrare che tante forme geometriche che si ripetono e formano altre figure che si ripetono con colori di forti e deboli per dare effetti e comunicare emozioni diverse..
Giorgia: Al centro c’è un cerchio, tutto parte da quel cerchio da cui partono altri cerchi più piccoli che si rimpiccioliscono via via , sembra che escano dal quadro come un effetto tridimensionale.
Fabio:Ci sono anche corone circolari e cerchi concentrici blu e rossi..
Nicoleta: Con le forme geometriche e l’uso dei colori contrastanti è possibile esprimere emozioni forti..
Tommaso. C’è un effetto ipnotico, la prima cosa che vediamo è la sfera che sporge ,ma se guardiamo l’insieme interamente senza concentrarsi sul particolare si vede la composizione di molte forme nell’insieme che stanno bene …in armonia.
Anita :Con le forme geometriche si possono fare disegni astratti e non e ci possono dare delle illusioni ottiche.
Noemy:Sembra l’universo che si espande e le forme si allontanano dal centro..
Bianca: Tanti quadrati che si espandono fino a formare un cerchio
Rob. E’ un’illusione ottica che ci fa sembrare che esce dal foglio
Nicoleta: Sembra il dopo- Big Bang quando le varie forme si allontanano con regolarità per formare i pianeti e le stelle che hanno la stessa origine e la stessa composizione …
Alessandro: Sì sembra proprio l’espansione dell’Universo con una sua regolarità…




