La creazione di Aya – Creazioni matematiche

Irene Vacca, classe quinta, Barzanò (LC)

La creazione scelta è quella di Aya che l’autrice spiega così:

Dopo aver discusso di questa creazione Aya offre ai compagni la sua spiegazione. Si parla di fare sempre la metà o fare sempre il doppio. Ma qualcuno afferma anche che basta aggiungere e togliere. Emerge il conflitto tra additivo e moltiplicativo ma anche il passaggio dalla divisione alle frazioni. La discussione ci porta verso una situazione problema che mette in gioco sia i concetti di divisione che di frazione.

Il muro delle creazioni

Dopo aver scelto e discusso la creazione di Aya, ho pensato a un modo per utilizzare tutte le altre creazioni.

Essendo in DDI, ho utilizzato Padlet per organizzare una “mostra delle creazioni”; l’abbiamo chiamato “IL MURO DELLE CREAZIONI”.

Ho pensato di proporre quest’attività con un duplice obiettivo: fare in modo che tutte le creazioni fossero condivise e permettere ai bambini di continuare ad allenare il proprio “occhio matematico”.

La consegna data agli alunni è la seguente:

A questo link https://padlet.com/irenevacca/x201diugjo1gdlfb puoi accedere al muro delle creazioni.
Scegli due creazioni e scrivi il motivo della tua scelta, seguendo queste domande guida:
– perché hai scelto questa creazione?
– cosa vedi di matematico?
– cosa diresti al tuo compagno che ha fatto la creazione?

Ecco le risposte degli alunni:

Ho scelto la creazione di Simone “il bicchiere matematico” perché, proprio come contrario della creazione di Camilla, qui tutti gli elementi matematici sono mescolati nella bibita del bicchiere. Ci sono tante cose matematiche per esempio i numeri, le frazioni, i numeri con la virgola, la famiglia dei litri e infine i segni delle operazioni. A Simone chiederei perchè ha fatto questa scelta, a me viene in mente un bicchiere magico pieno di conoscenze matematiche che se lo bevi tutto impari tutta la matematica in un solo sorso! FRANCI

Ho scelto quella di Simone perchè secondo me è vero quello che vuole rappresentare cioè che in un bicchiere d’ acqua non è così scontato che ci sia tanta matematica. Secondo me di matematico c’è tutto, ma in particolare i l, ml, dl… Vorrei chiedere a Simo cosa stanno a significare i numeri messi all’interno del bicchiere e se sono stati messi a caso. VERA

Mi ha colpita molto la creazione di Stella, perchè è interessante. Vorrei dire che anche se capovolgiamo la creazione l’altezza può cambiare; per quello ci conviene utilizzare i grammi! L’altezza può cambiare, ma la quantità no. AYA

Le mie creazioni preferite. Ho scelto le creazioni di Stella e Citty perché hanno lo stesso scopo di rappresentare l’equivalenza, infatti hanno:
-usato gli stessi elementi (pasta e farro)
-volevano rappresentare la stessa cosa (ovvero che una quantità di qualsiasi cosa può essere rappresentata in modi diversi).
A Stella e Citty vorrei dire che le loro creazioni sono chiare e si capiscono bene. FABIA

Per quella di Samah ho solo da dire che ha messo la matematica ma soprattutto quello che abbiamo fatto: le equivalenze, le frazioni….. AYA

La mia creazione preferita è quella di Samah: Nella creazione di Samah vedo di matematico:
I numeri
Le unità di misura(g, d…)
Le frazioni (⅓ ⅘)
AIDA

Ho scelto la creazione di Samah; io di matematico nella sua creazione ho visto le frazioni e che ha usato le varie misurazioni. ARIANNA

Ho scelto quella di Davide e Corti, perchè, sono molto chiare. Di matematico in quella di Davide vedo che ha usato i litri e li ha distribuiti in un bicchiere. E in quella di Corti vedo la stessa cosa di Davide è solo che Corti li ha distribuiti in cubi. Ai miei compagni gli direi che sono stati molto bravi, perché, quelle creazioni si capiscono! SAMU

Ho scelto questa creazione di Corti perché mi ha colpito la grafica che ho usato. Di matematico vedo i litri. Gli chiederei perchè ha scritto 300/500/1000. DAVIDE

Di matematica io vedo i grafici e i litri. Ho pensato che se il cubo più piccolo fosse da 250 dl, tra tutti i contenitori ci sarebbe un rapporto che, dal più piccolo al più grande sarebbe del doppio, mentre, dal più grande al più piccolo sarebbe della metà. Di geometria, invece osservo la presenza di tre cubi disegnati in 2D. Vorrei chiedere ad Andrea se nei cubi le tacche sono state fatte con un ordine preciso o a caso. CITTY

Ho scelto la creazione di Andrea Corti perchè ha avuto un’idea simile alla mia. Viene rappresentato un istogramma dove vengono riportate le quantità di acqua presente nei cubi. Le tacche verticali rappresentano i dl che vanno di 100 in 100. Di matematico vedo l’unità di misura dei litri, il grafico e la rappresentazione dei cubi. Ad Andrea chiederei con quale altro grafico vorrebbe rappresentare questa situazione. CAMI

La creazione di Corti l’ho scelta perchè era molto ordinata e molto chiara da comprendere rispetto ad altre. Di matematico vedo un istogramma, i numeri, le unità di misura del l in particolare i dl e qualcosa anche di geometrico cioè i cubi. Non gli chiederei nulla perchè il suo lavoro mi sembra completo. NICHOLAS

Ho scelto la creazione di Arianna perchè ci sono rappresentate due operazioni: la moltiplicazione e la divisione. Nella divisione 25:3 compare il numero periodico 8,3333… viene messo in evidenza il fatto che il 10:3 come risultato è 3,3 periodico. Per quanto riguarda la moltiplicazione mette in evidenza tutte le prove che ha fatto per trovare un numero che si avvicini come risultato a 25 tenendo sempre come moltiplicatore il numero 3 e per questo motivo ha messo le parole alto, basso e si avvicina. Direi ad Arianna che ci ha messo alla prova ed è stata molto astuta. CAMILLA

Ho scelto questa creazione perché è dalla mia amica Fabia . Vedo di matematico delle frazioni. Poteva mettere le scatole di riso e di farro per far capire l’intero ¼ di scatola di riso e ⅔ di scatola di farro. La seconda creazione che ho scelto è quella di Fabia perché è molto originale. Di matematico ci sono le quantità dentro ad ogni contenitore rappresentate dalle frazioni. Vorrei dire alla mia compagna che è stata molto brava. COSTANZA

Ho scelto questa creazione perché è un esempio pratico di come la matematica si possa applicare alla realtà. Osservo che ¼ si riferisce alla quantità di riso contenuto rispetto alla ciotolina, mentre 2/3 si riferisce alla quantità di farro e cioccolato rispetto alla ciotolina. Vorrei chiedere a Fabia se ha diviso le quantità approssimativamente oppure in modo preciso. ANDREA CITTY

Secondo me Fabia ha voluto rappresentare una retta dei numeri perchè i bicchieri indicano le tacchette e una tacchetta vale ⅔ e un’altra ¼. PRINCE

(Costanza, alla fine del tempo per realizzare la creazione, ha detto che non era riuscita a metterci la matematica)

La mia prima creazione preferita è quella di Costanza perché anche se lei crede che non ci sia matematica nella creazione, io sono sicura che qualcosa di matematico ci sia. Ecco cosa vedo di matematico della creazione di Costi: le unità di misura (la quantità degli elementi che la compongono), la L di litri o la G di grammi fatta con la pasta sopra la creazione. L’unica cosa che vorrei chiedere alla Costi è: “Perché credi che non ci sia matematica nella creazione???’’ STELLA

Ho scelto la creazione di Nicholas, perchè di matematico vedo: se sommo e moltiplico i numeri il risultato è 6, i disegni di geometria sono 6 e le equivalenze contengono il numero 6. È stata un’ottima creazione! ALESSIA

Come prima creazione ho scelto quella di Nicholas perché c’era il +,×,– e c’era anche un trapezio, le unità di misura ma avevo anche qualche dubbio su quello che ha scritto: “chi? cosa? ecc.” non ho capito molto bene quello che intendeva con quelle scritte. AMINA

La seconda creazione che ho trovato interessante è quella di Prince perché secondo me racchiude sia matematica e sia la geometria. Di geometrico vedo le forme invece di matematico vedo le unità di misura e un 8. L’informazione che vorrei sapere è: “Che cosa sono quelle ali che ha l’8’’ STELLA

Ho scelto questa creazione perchè quando l’ho vista mi ha colpito molto e mi ha fatto ragionare tantissimo per capire che senso avesse quella creazione e dopo qualche oretta (forse) ho capito cosa volesse rappresentare. Vedo di matematico molte cose ad esempio l’otto in mezzo, il triangolo e il trapezio dentro un otto capovolto ai lati, i litri e i chilometri e molte altre cose. Chiederei a Prince di potermi spiegare se i cerchi con dentro il trapezio e il triangolo sono i due cerchi dell’otto capovolto. ANDREA CORTI

Nella creazione di Camilla vedo di matematico:
I numeri
Le unità di misura (dl, l, hl, ml…)
I grafici
AIDA

Io di matematico della sua creazione ho visto che voleva rappresentare la trasformazione tra i vari grafici. Poi ho visto che ha usato sia i grammi che i litri. ARIANNA

Io ho scelto la creazione di Camilla perchè ha trasformato l’immagine del cocktail in grafici e seconde me è una cosa divertente. Di matematico vedo i grafici (istogramma e torta), la suddivisione grafica del cocktail (in realtà non potrebbe esistere perché i liquidi si mischierebbero) e un’equivalenza della somma dei vari liquidi da dl a l. Io farei i complimenti a Camilla perchè tutto quello che ha rappresentato è collegato e vorrei chiederle come gli è venuta in mente questa bellissima idea. FRANCESCO

Quella di Camilla l’ho scelta perchè mi piaceva come era disposta sul foglio e mi incuriosiva molto. Nella sua creazione vedo, di matematico, prima di tutto i grafici che ha usato cioè l’istogramma e il grafico a torta, poi vedo i numeri e le unità di misura dei litri in particolare i dl e i l. L’unica cosa che le chiederei è perchè alla fine ha trasformato i dl in l e invece non ha tenuto la stessa unità di misura. NICHOLAS

Camilla ha usato i dl e i grafici dalla sua creazione vedo che:
la limonata ha la quantità’ maggiore di liquido
per ogni bibita ha usato la quantità’ di cibo corrispondente es.
5 chicchi di riso =5 dl
3 chicchi di farro = 3 dl
2 sedanini = 2 dl
9 chicchi di farro = 9 dl
SIMONE

Come prima creazione ho scelto quella di Camilla perchè mi piace come l’ha rappresentata, ma soprattutto perchè ha mischiato grafici, litri e grammi. Di matematico vedo tutto perchè non esiste cosa dove non c’è la matematica, ma in particolare l’istogramma ed il grafico a torta o areogramma. A Cami chiederei perchè ha messo così pochi chicchi di riso per rapresentare l’aranciata, se berrebbe il miscuglio o se è commestibile, se le quantità sono a caso o se sono state calcolate per poterlo fare e perchè non ha usato i litri. VERA

Ho scelto la creazione di Andrea Citterio, perchè di matematico vedo le equivalenze; ha trasformato gli ettolitri in decalitri e in litri. È stata una bella creazione! ALESSIA

Ho scelto la creazione di Andrea Citterio perché mi è piaciuto il percorso che ha fatto con l’unità di misura. Di matematico vedo un’unità di misura: i litri. Gli chiederei perché ha voluto rappresentare il passaggio da centilitri a decilitri e da litri a decalitri. DAVIDE

Ho scelto le creazioni di Stella e Citty perché hanno lo stesso scopo di rappresentare l’equivalenza, infatti hanno:
-usato gli stessi elementi (pasta e farro)
-volevano rappresentare la stessa cosa (ovvero che una quantità di qualsiasi cosa può essere rappresentata in modi diversi).
A Stella e Citty vorrei dire che le loro creazioni sono chiare e si capiscono bene. FABIA

Ho scelto la creazione di Citty perchè mi sembrano delle lettere scritte con l’alfabeto egiziano. Di matematico vedo i numeri e le trasformazioni della famiglia dei litri. Direi a Citty che il suo lavoro mi è piaciuto e mi ha colpito molto come ha rappresentato la famiglia dei litri. CLAUDIO

La prima creazione che ho scelto è quella di Alessia perchè è schematica ma semplice. Di matematico ci sono le misure di lunghezza e di capacità. Vorrei dire alla mia compagna che si potevano inserire anche delle equivalenze. MATTEO

A me è piaciuta molto quella di Alessia perchè:
-ho scelto questa creazione perchè appena vista mi ha incuriosito molto e mi ha spinto a ragionare su che cosa volesse rappresentare esattamente.
– di matematico vedo sia i LITRI che i METRI ma anche un RETTANGOLO. Secondo me ha voluto rappresentare una partita di pallavolo che giocavano i litri contro i metri di cui lei era l’arbitro.
– chiederei ad Alessia se davvero voleva rappresentare una partita di pallavolo, perché ha messo alcune uguaglianze (ad esempio 3 cl=3 m) e vorrei inoltre sapere chi ha vinto tra i litri e i metri questa fantastica sfida ANDREA CORTI

Ho scelto la creazione di Alessia perchè mi è sembrato di vedere un campo da calcio o da pallavolo con dei giocatori, i litri contro i metri. Di matematico vedo le famiglie dei litri e dei metri. Direi ad Alessia che mi sembra di vedere dei giocatori con i numeri sulla maglietta. CLAUDIO

Situazione problema: La lepre marzolina

La situazione nella sua versione originale:

La-Lepre-Marzolina-scheda-alunno Download

LA LEPRE MARZOLINA

I bambini hanno cercato la soluzione in autonomia. Di seguito, ciò che hanno scritto i bambini sul loro quaderno.

Ho raccolto le strategie e le ho riassunte.

Questa settimana ho mostrato loro queste strategie riassunte, ho chiesto loro in quale si ritrovassero e abbiamo discusso quali potevano funzionare e quali no. Abbiamo cercato anche analogie e differenze tra le strategie.

Successivamente abbiamo pensato a come rappresentarle graficamente: prima ci siamo dedicati al cibo e poi al tè; anche durante questa attività ci siamo soffermati sulle differenze tra l’operare con 9 tartine/rotolini/vasetti e operare con i 9 cl.

Consegna: “Come risolverà il problema la Lepre Marzolina? Riuscirà a non far avanzare nulla?”

QUINTA A

Secondo me la Lepre Marzolina può dare a tutti una porzione e mezza così non rimane niente. Ho tracciato una linea ogni porzione e mezza e così non rimane niente. FRANCI

Secondo me la Lepre Marzolina dovrà fare 9 centilitri diviso 6 tazze:

9:6= 1,5. Così ognuno avrà 1,5 cl di tè.

Potrebbero fare lo stesso con le tartine, la marmellata e i rotolini di burro: daranno 1,5 di tartina,1,5 di vasetti per ciascuno e 1,5 rotolini di burro ad ognuno. ANDREA

9:6=1,5

Per me per dividere il tè, la Lepre Marzolina deve fare 9 che sono i cl diviso 6 che sono le persone e fa 1,5. Ognuno berrà 1,5 cl di tè.

Per non far avanzare il cibo, ognuno dovrà mangiare 1,5 di tutto, perché 1,5×6= 9. Quindi non avanza niente. CAMI

La lepre risolverà la situazione dando a ciascuno 1,5 di tè, di tartine, di vasetti di marmellata e rotolini. Ho pensato a 1,5 perché ho fatto 9:6=1,5. ARIANNA

[Cosa significa “1,5 di tartina”? Questo ha acceso la conversazione sul ciò che c’è di diverso quando ragioniamo con le 9 tartine e quando ragioniamo sui 9 cl.

Citty ha riassunto dicendo: “Anche io ho usato questo ragionamento, ma 1,5 va bene per i centilitri. Per generalizzare con il cibo ho detto una quantità e mezza.”]

La lepre potrebbe dare a ogni partecipante 1,5 cl. Ecco perché:

9 cl :6=1,5cl

E, per non far avanzare niente, basterà dare anche per la marmellata, le tartine e il burro una quantità e mezza. CITTY

Sapevo che le tartine erano 9 e gli invitati 6, perciò ho fatto 9:6=1 resto 3

Ho pensato di dividere il 3 di resto: venivano 6/2.

questo modo di porre la soluzione va attentamente discussa perché 3:6=0,5 cioè ½ non 6/2, perché Vera dice che trova 6/2? perché ha preso 3 porzioni e di ciascuna ha fatto la metà quindi ha fatto 2/2 + 2/2 + 2/2

la scrittura 6/2 traduce in simboli le parole sei mezze porzioni (vedi Samah)

A ogni tartina ho aggiunto ½. VERA [ragiona con le frazioni]

Se i personaggi sono 6, dobbiamo dividere il tè in 6 facendo 9:6. Per comodità però io ho deciso di trasformare 9 centilitri in 90 millilitri e fare 90:6 che fa 15. così evita di fare la divisione con il divisore maggiore che dà sempre fastidio, ma questo con i rotolini di burro non si può fare, mi sembra un buon aggancio

Cara lepre Marzolina, per dare la stessa quantità di tè a tutti dovrai versarne 15 ml a ciascuno. Buon tè!

Per non far avanzare cibo, la lepre deve prima dare a ciascuno 1 tartina e ne avanzeranno 3 (dato che sono 6 e le tartine sono 9).

Dovrà fare 3:6= 0,5.

Ognuno prenderà mezza tartina. SAMAH [qui noto che c’è proprio l’idea del distribuire] ma anche prima c’era altrimenti non avrebbero ragionato in quel modo, chiedi cosa vuol, dire “dividere” e avrai i diversi significati

Lepre Marzolina, io farei così: dividere i centilitri di tè: 9:6 = 1

Per le tartine, sempre uguale e anche per gli altri cibi.

Devi dividere per forza per 6 perché ci sono sei persone che devono bere il tè oppure mangiare.

Avanza sempre 3 di tutto. che cosa ne facciamo? CLAUDIO [non considera il resto]

Lepre Marzolina, io farei così: per far mangiare a tutti la deliziosa merenda io dividerei tutto il cibo sulla tavola (cioè 36) per il numero delle persone che devono mangiare la merenda (cioè 6).

36:6= 6

Così tutti hanno mangiato la merenda. AIDA [non considera che tutti devono mangiare la stessa quantità di ogni cibo e di tè]

La mia idea è che ad ognuno va metà di ogni cosa, quindi così:

½ di tartina ad Alice, ½ al coniglio, ½ al gatto, ½ alla lepre, ½ al cappellaio e ½ al ghiro…

Il ragionamento che ho fatto è lo stesso per tutto ciò che c’è sul tavolo. SIMONE

[questo ragionamento che non dà una soluzione corretta ha aperto, però, alla visione di un’altra possibilità: dividere ogni tartina a metà e distribuire ½ di tartina ad ogni personaggio, fino a finire le tartine. In questo modo riusciamo a capire che ogni personaggio avrà 3/2 di tartine, rotolini, vasetti e che 3/2 corrisponde a 1 intero e ½] ottimo!

Lepre Marzolina, io farei così:

per il tè sono andato un po’ a tentativi e infine ho capito che era 1,5. Poi però ho trovato una tecnica: mi sono immaginato una retta e ho fatto come in classe, sono arrivato a 9 e ho diviso per gli spazi che erano 6. E poi ho capito che l’operazione era 9:6

Ovviamente per le altre cose è uguale perché gli interi sono sempre 9 e dobbiamo dividerli sempre per 6. NICHOLAS [idea della RETTA DEI NUMERI, questa strategia può essere utilizzata per un ulteriore passaggio concettuale per la classe?] direi proprio di sì, è importantissimo passare da una sistema all’altro

QUINTA B

Ho pensato di dare a ciascuno una tazza, una tartina, un vasetto di marmellata e un rotolino di burro.

Rimarranno 3 cose di qualunque cibo e ho pensato di dividerli a metà; quindi una persona prenderà:

1,5 cl di tè
1 tartina e mezza
1 vasetto di marmellata e mezzo
1 rotolino di burro e mezzo

Infine tutti ingrasseranno della stessa quantità. AYA [idea del distribuire, il finale comico ha sotto un’idea importante: dare ad ognuno la stessa quantità, che abbiamo ricordato più volte durante il confronto e che è chiara ai ragazzi]

Se ci sono 9 tazzine per sei persone, ognuno può averne 1 e condividere 1 tazzina con un altro; così tutte le tazzine sono prese.

Poi se ci sono 9 tartine, ognuno ne prende 1 e le altre 3 rimanenti si dividono a metà e si ottengono 6 pezzi e se ne distribuisce 1 a ognuno e ne avranno 1 e mezzo.

Così anche per i rotolini di burro. Poi per la marmellata, ognuno prende 1 vasetto e un altro lo condivide con un altro personaggio. Infine per i 9 cl d’acqua ognuno ne beve 1 cl e 5 ml. FABIA

[anche qui emerge l’idea del distribuire. Questa spiegazione ci ha permesso di riflettere sul linguaggio. Non a tutti era chiaro, allora abbiamo provato ad aggiungere delle parole “matematiche”, sostituendo “ 6 pezzi” con 6 metà oppure sei mezzi; la frase “ne distribuisce 1 a ognuno” è stata modificata con “ distribuisce ½ (oppure metà) tartina a ognuno” anche qui tornano le frazioni] molto bene, è importante distinguere “pezzo” da “metà” ma non bisogna nemmeno perdere il riferimento al fatto che si tratta di metà di qualcosa, sono parti di…. non parti e basta

Se i partecipanti sono 6 dà ad ognuno 1 cibo e avanzeranno 3 di ogni cibo. Quindi basta dividere ogni cibo un’altra volta; quindi ci sarà 6 [6 cosa? Manca la precisione del linguaggio; il discorso affrontato con la spiegazione di Fabia si collega anche a questa spiegazione] di ogni cosa e avanzerà 0 di ogni cosa.

Per il tè rimarranno 3 centilitri di tè quindi se ogni centilitro lo dividiamo per 2, usciranno 5 millilitri in più per tutti e non avanzerà nulla. DAVIDE [come Fabia, passa in modo spontaneo dai cl ai ml]

Io ho pensato di fare 9:6 che fa 1,5, quindi per dividere la merenda e darla a tutti, ogni cosa devi farla da 1,5. SAMU [questa strategia, utilizzata anche da altri compagni, ci ha permesso di iniziare a riflettere sul fatto che ci sia una differenza tra dividere le 9 tartine e dividere il tè. Stella dice: “Per il tè ha senso dire 1,5 cl; ma con le tartine no. Cosa vuol dire 1,5 di tartina. Devo usare le frazioni”. Si tratta di una differenza che viene percepita ma che si fatica a spiegare]

Se noi abbiamo 9 tartine, 9 tazzine, 9 vasetti di marmellata, 9 rotolini di burro e 9 centilitri di tè. Per farli diventare per 6 persone, 9 centilitri di tè dobbiamo farli diventare 90 ml.

90ml :6=15 ml

I nostri 15 ml di tè dobbiamo trasformarli in centilitri; quindi saranno 1,5 cl. [anche qui c’è il passaggio da un’unità di misura all’altra, ma per il cibo? Anche questo si è collegato alla strategia di Samu]

Due alunne non hanno trovato la soluzione alla situazione.

queste due bimbe non le dobbiamo abbandonare, diamo loro in mano gli oggetti veri e facciamoglielo fare concretamente, se porti le cose a scuola o fai un filmino in cui le mostri davvero potrebbe essere utile anche come conclusione per gli altri e per rilancio sul 12…

quelli che dicono subito che 9:6=1,5 come fanno il calcolo? usano la calcolatrice o hanno altre strategie?

E se i partecipanti fossero 12?

Alcuni esempi di protocolli degli alunni con diverse strategie:

Il conflitto additivo moltiplicativo

OBIETTIVO: CONFRONTARE LA VISIONE MOLTIPLICATIVA E LA VISIONE ADDITIVA – IDEA DELLA SOTTRAZIONE

Stella: secondo me invece c’entrano le unità di misura perché se non sbaglio prima ha utilizzato la caraffona con le misure. Secondo me ha utilizzato sempre gli stessi ingredienti però nel primo ha utilizzato un tot di farro; nel secondo ha utilizzato sempre il farro, solo che ne ha usato di meno. Ha utilizzato le unità di misura per capire…per dare un senso…come si dice..

M. Irene: prova, poi magari qualche compagno ti aiuta

Stella: eh va tipo a scala

M. Irene: a scala

Davide: eh sì così: dal più piccolo al più grande

Ale: no dal più grande al più piccolo

Fabia: è uguale

Stella: ecco cosa volevo dire: secondo me di sicuro ha utilizzato una misurazione. Tipo i centimetri, penso, per vedere l’altezza.

M. Irene: quindi secondo te l’unità di misura che ha utilizzato sono i centimetri

Stella: secondo me sì. Poi ha calcolato qualcosa e ha pensato: lì metto un numero tipo 15 e ha sempre sottratto il 5. E ha fatto 10, 5 e lì…..

DIVISIONE E SOTTRAZIONE

M. Irene: quindi secondo te ha sottratto. Davide ha detto che ha fatto la metà della metà della metà; cosa ha fatto?

Fabia: ha diviso

M. Irene: cambia o è la stessa cosa?

Fabia: forse è la stessa cosa

Cos: eh no perché dividere significa che c’hai..

Ale: una quantità

Cos: una quantità e la devi dividere. Sottrarre non è uguale.

M. Irene: e cosa c’è di non uguale?

Samu: se dividi, dividi per due. Se fai meno, fai meno un pezzettino.

M. Irene: Proviamo a rispiegare… Samu dice: se ho una quantità la divido in due parti, come?

Samu: uguali. Se sottraggo, tolgo quanto voglio. Però Stella ha un po’ fatto anche la divisione. Cos’avevi detto? 15?

Stella: eh ma con 15, l’ultimo rimane 0.

Samu: ha fatto come 15:3

Stella: era meglio utilizzare il 20. Perché quello lì è 20, quello diventa 15, poi 10 e 5.

Davide: è come fare 20:4

M. Irene: in che senso?

Fabia: secondo me è fare la stessa cosa sì e no: è la stessa cosa “Sì” perché se hai un numero tipo 20 e dividi per 4 e trovi 5, poi fai meno 5, meno 5….. ora ti dico perché “no”: perché con la divisione se fai 20:4, arrivi direttamente a un numero, con la sottrazione devi fare tutti i passaggi.

Samu: fare 20:4 è come fare 20-15. Se fai 20:2 è diverso che fare 20-2

M. Irene: è molto diverso

Canovaccio della discussione

PARTENDO DAL PIÙ PICCOLO, FARÒ SEMPRE IL DOPPIO DEL PRECEDENTE…. PARTENDO DAL BICCHIERE PIÙ GRANDE, FARÒ SEMPRE LA METÀ
PARTENDO DAL PIÙ GRANDE, SOTTRAGGO SEMPRE LA STESSA QUANTITÀ.

DOMANDE PER LA DISCUSSIONE:

NOTATE DELLE DIFFERENZE TRA QUESTE DUE IDEE?
QUALE OPERAZIONE STIAMO FACENDO NEL PRIMO CASO E NEL SECONDO CASO?
OSSERVANDO LA CREAZIONE DI AYA, SECONDO VOI, CHI HA RAGIONE?
IMMAGINATE DI PREPARARE I QUATTRO BICCHIERI: COSA VI SERVE SAPERE PER ORGANIZZARE I BICCHIERI SECONDO LA PRIMA REGOLA? E SEGUENDO LA SECONDA REGOLA?

Di questa discussione non c’è la trascrizione.

Dopo la Lepre Marzolina

Dopo la Lepre Marzolina

Le situazioni problema sviluppate dopo quella della Lepre Marzolina

Dal macellaio (detto anche “Il problema del prosciutto“)

Luca e Francesca si trovano in macelleria.
“Ciao!”, dice Luca, e intanto paga alla cassa con una banconota da 20 euro i 3 etti di prosciutto crudo che ha comprato.
Francesca dice: “Anch’io sono venuta a comprare il prosciutto, la mamma mi ha detto di comprarne una fetta da 0,6 etti e mi ha dato questi soldi” e mostra a Luca le monete che ha in mano: 1,50 euro.
“Non ti basteranno!”, dice Luca, “guarda in vetrina: il prosciutto costa 2 euro l’etto”
Pensate che Luca abbia ragione? Date le vostre risposte e spiegate perché.

Il puzzle di Brousseau

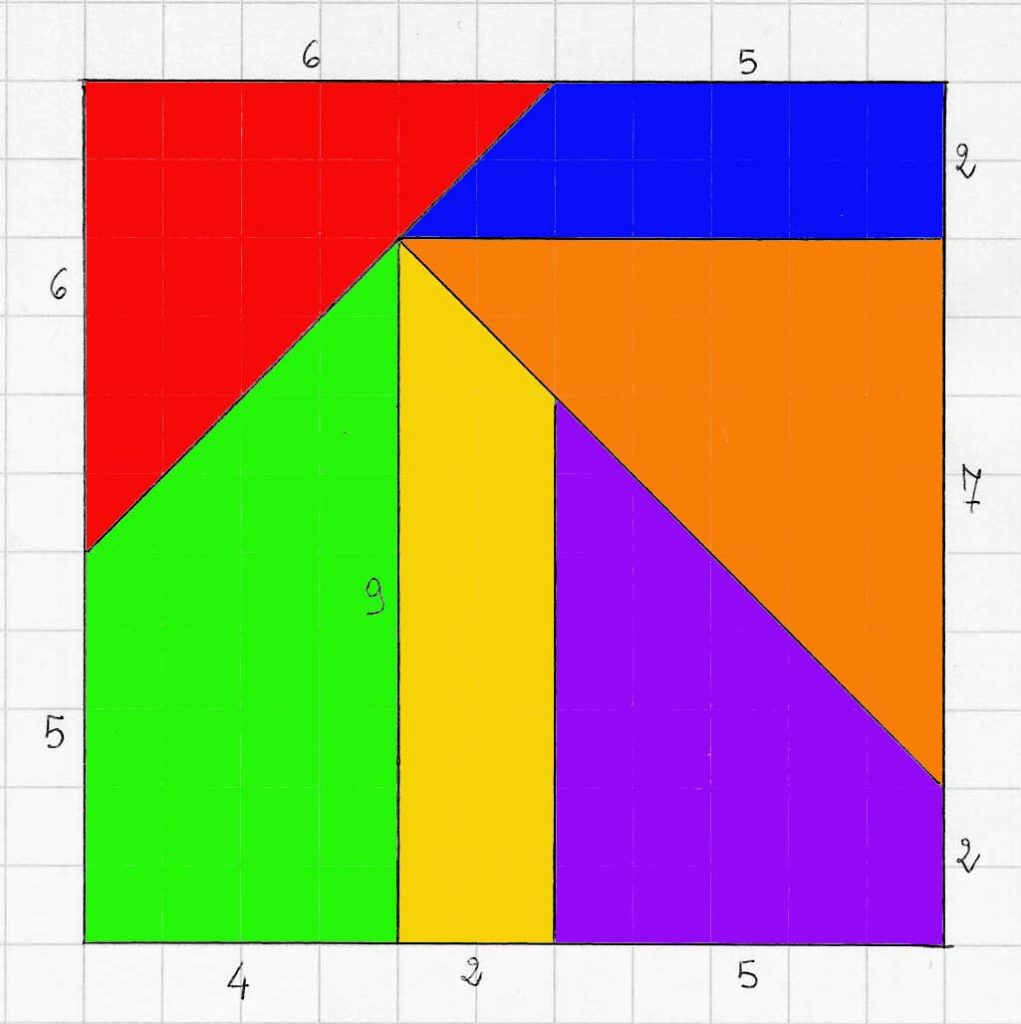
MATERIALI

puzzle da ingrandire (il disegno qui sopra serve solo come modello ma non va usato per risolvere il problema), carta a quadretti, forbici, righello, matita…

CONSEGNE

Disponetevi in gruppi di 6. Ogni persona del gruppo deve fare l’ingrandimento di un pezzo di questo puzzle. La regola è questa: il lato del pezzo che misura 4 cm, sul puzzle ingrandito dovrà misurare 7 cm. Alla fine si deve ricostruire il puzzle ingrandito.
Dopo la realizzazione dei 6 pezzi il gruppo discute dei metodi utilizzati. Se il puzzle non si può ricostruire perché i pezzi non combaciano, il gruppo cerca un nuovo metodo e ognuno ricostruisce il suo pezzo.

Tag: conflitto additivo-moltiplicativo, proporzionalità