Sonia Sorgato, classe terza, Milano
Il percorso
- Discussione della creazione matematica della scaletta di Alessandro
- Idee emerse dalla discussione: gli sviluppi del cubo e le foto cambiano la forma
- Attività sugli sviluppi del cubo con materiale a incastro
- Uscite nel quartiere e rappresentazione dello spazio del parco da diversi punti di vista e provando a immaginare lo spazio dall’alto
- Discussione su che cosa comporta disegnare gli oggetti dall’alto: il
drone e riflessione sul filmato - Nuova creazione con materiale a incastro
Creazione matematica di Alessandro
Ottobre 2020
Insegnante: oggi inizieremo con una discussione sulla creazione matematica di Alessandro, solo alla fine Alessandro che è l’autore potrà intervenire.
Sara: io lo so cosa diventa…
Omar: una scala!
Matteo: lo so cosa diventa!
Davide: a me vengono in mente delle cose!
Arianna: è un quadrato, cioè può diventare un quadrato (la creazione si può piegare per formare un quadrato).
Cloe: da una scala diventa un cubo.
Insegnante: diventa un cubo?
Alessandro: no, non è un cubo!
Insegnante: ci ha dato una bella idea Cloe.
Alessandro: può diventare un cubo.
Cloe: ti faccio vedere (fa il gesto di piegare carta per ricomporre uno sviluppo di un solido).
Matteo: un cubo è un solido, lo puoi toccare, questo è come un foglio origami, non ha lo spessore.
Alessandro: il foglio ha lo spessore.
Antonio: cos’è lo spessore?
Insegnante: proviamo a rispondere alla domanda di Antonio.
Jana: questo è uno spessore (indica la dimensione più piccola del foglio).
Solayman: è il foglio che da questa parte ha lo spessore.
Cloe: vedi la gomma? Questo è uno spessore (indica una dimensione della gomma). Vedi il foglio? Ha un piccolissimo spessore ma ce l’ha.
Sara: anche le orecchie del gatto hanno uno spessore.
Cloe: anche il banco ha uno spessore, la testa di Matteo, la mascherina…
Jana: anche la nuvola…
Insegnante: Matteo, tu mi parlavi di cubo e di quadrato, che differenza c’è?
Matteo: è come un disegno in 3D, il quadrato è un disegno, è una forma però…se disegni un cubo anche se non lo puoi prendere, ma nel disegno si vede che lo puoi prendere e c’è una differenza…
Insegnante: qual è la differenza?
Matteo: il cubo ha 6 lati.
Solayman: si chiamano facce.
Matteo: il quadrato ne ha 4.
Alessandro: ha delle linee.
Giorgio: si chiamano segmenti.
Insegnante: abbiamo detto molte cose: abbiamo detto che il cubo ha 6 facce e si può prendere in mano come ha detto Matteo, il quadrato…
Jan Paul: il quadrato è fine.
Alessandro: il quadrato si spezza subito.
Omar: il quadrato è nell’immaginazione.
Cloe disegna alla lavagna un quadrato e un cubo (2 rettangoli affiancati).
Sveva: può diventare un cubo perché ci sono 3 quadrati.
Insegnante: servono 3 quadrati?
Sveva: ne servono 6.
Insegnante: avete visto cose molto interessanti che dovremmo verificare. Antonio ha sempre il dubbio di cosa sia uno spessore.
Alessandro: prova a mettere così la mia creazione (indica di cambiare la posizione del foglio).
Stefany: può essere una scala.
Jana: il foglio uno spessore ce l’ha.
Cloe: veramente il foglio ha 4 spessori!
Insegnante: siete d’accordo? Quanti sono gli spessori del foglio?
Alessandro: sono 6 spessori. Forse sono 5 spigoli.
Insegnante: cerchiamo di capire: questi sono i lati.
L’insegnante mostra l’altezza, larghezza e profondità di un mobile… si riutilizza la parola dimensione.
Insegnante: il quadrato della lavagna quante dimensioni ha?
Sveva: 2 dimensioni!
Alessandro: è come una croce.
Matteo: ma lo spessore come è fatto?
Alessandro: lo spessore è la distanza dal muro.
Davide: questo inizia da su e poi va giù, sembra una giraffa.
Arianna: ci sono 3 forme uguali che sono una sopra l’altra. Sono rombi.
L’insegnante prende un foglio origami.
L’insegnante: questo che forma ha?
Sveva: è un quadrato, se abbiamo iniziato con un quadrato non può cambiare forma se lo giro.
Insegnante: rimane sempre un quadrato, però possiamo dire che il quadrato è un rombo particolare.
Jana: se facciamo una foto a un quadrato può diventare un rombo.
Insegnante: le foto cambiano le forme delle cose. Ascoltiamo ora l’autore della creazione.
Alessandro: la creazione può diventare un quadrato se lo pieghi.
Cloe durante la discussione ha creato uno sviluppo del cubo e lo mostra ai compagni.
Creazioni successive alla discussione

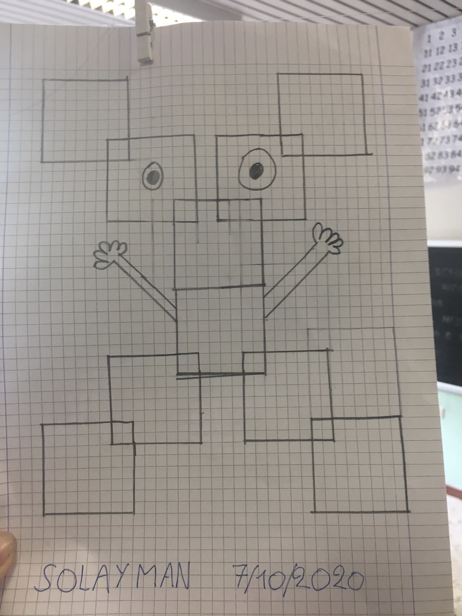

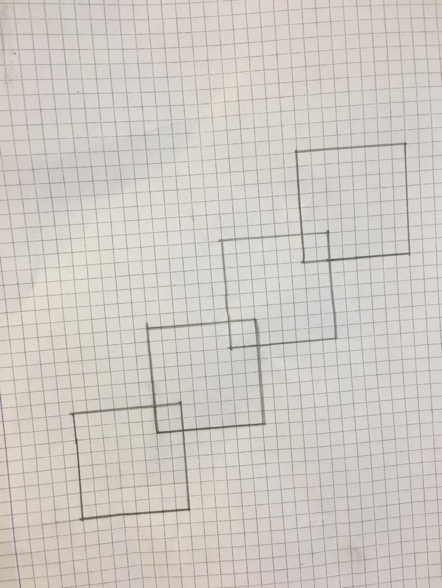

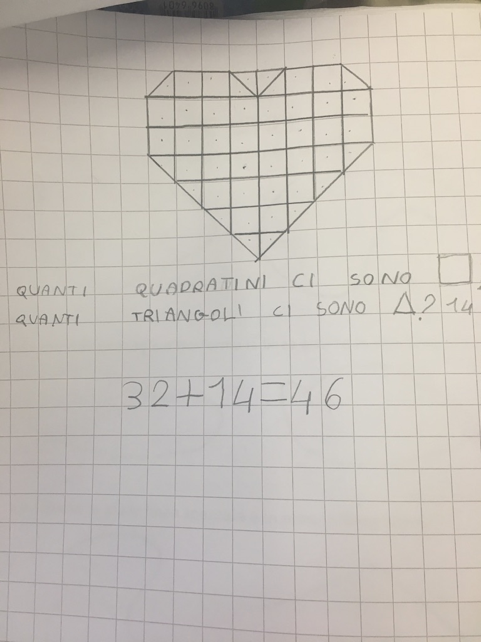

Idee per la progettazione
-ripresa dei termini utilizzati dai bambini durante la discussione per una maggiore sistematizzazione (dimensioni, lati, segmenti, spigoli…),
-attività su rombo e quadrato con cannucce e fili (Castelnuovo) o utilizzando le foto come suggerito da Jana (l’anno scorso abbiamo lavorato sulle ombre),
-sviluppi del cubo,
-la 4° dimensione (l’ipercubo),
-area (dalla creazione del cuore).
Il drone (in collegamento con l’attività di geografia)
Vedere dall’alto cambia le forme? Che cosa fa vedere e che cosa non fa vedere la vista dall’alto? Le forme tridimensionali diventano piatte? Che cosa si nasconde “sotto” che non vediamo? E se prendiamo una forma piana come possiamo ricostruire una forma solida?
La creazione matematica di Malik
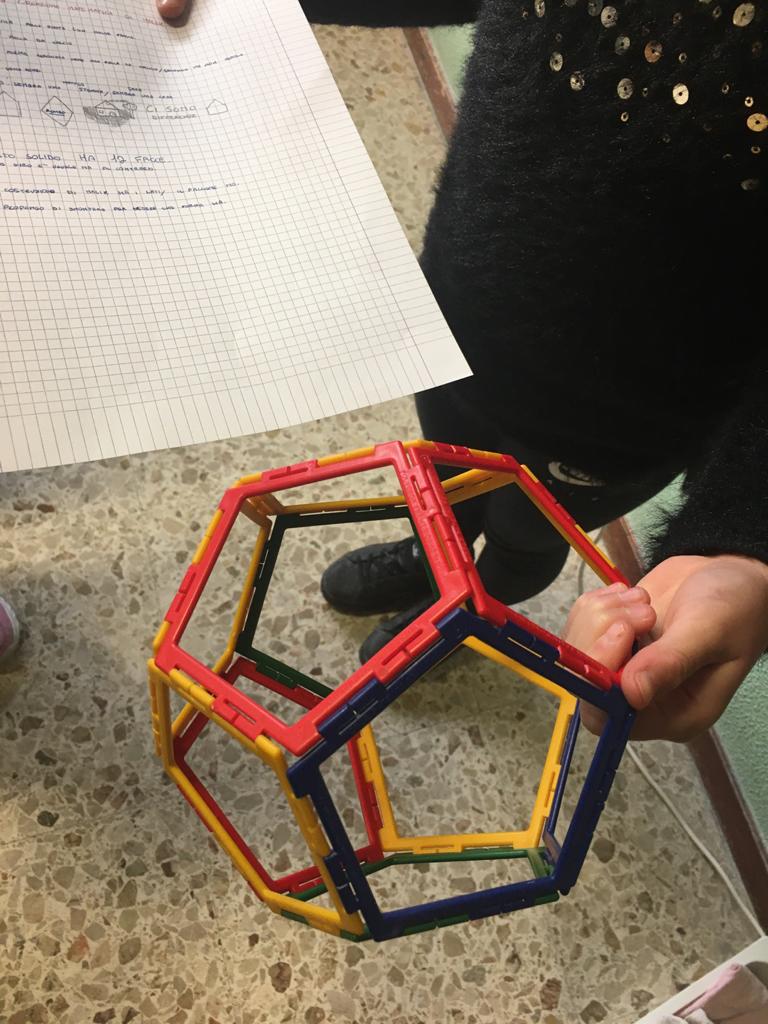
Maestra: oggi discutiamo rispetto alla creazione di Malik (1).
Solayman: mi sembra una palla piatta con molte facce.
Ale: non ha una forma cerchiata come la palla da calcio, secondo me non rotola come la palla da calcio.
Sveva: le facce sono rombi.
Matteo: sembrano uno stemma.
Sara: sembra una casa, ma la casa è diversa.
I bambini disegnano alla lavagna il pentagono del dodecaedro e il rombo per individuare le differenze, si accorgono anche che ci sono differenze fra il pentagono della casa e il pentagono regolare.

Ginevra: se metti il tetto e la porta diventa una casa.
Antonio: sembra un diamante. Non è un rombo.
Ale: ci sono delle differenze. Io ho scoperto una cosa del disegno che ha fatto Cloe, se lo metti al contrario, non come una casa anche se sembra, se la metti al contrario, la capovolgi diventa un diamante.
Alessandro: è una palla ma non è proprio una palla, ha degli angoli, dei lati. La palla ha tanti angoli e tanti lati.
Maestra: dobbiamo metterci d’accordo su che sono i lati e i gli angoli.
Ale: i lati sono questi (indica i vertici del solido) ma Malik non li ha fatti perché il materiale è fatto così, è una costruzione a incastro. Un pallone vero non li avrebbe questi punti perché sarebbe tutto rotondo.
Jana: quando giriamo a sinistra o a destra diventa un’altra cosa, una casa al contrario.
Ginevra: non cambia la forma.
Solayman: forse Jana vuole dire che si può ruotare la forma.
Jana: ha 12 facce!
Maestra: abbiamo scoperto un’altra cosa: ha 12 facce.
Jana: anche se lo giro è sempre lo stesso ma al contrario.
Ginevra: Jana, perché non è che se la Sonia si gira o si sdraia diventa un’altra persona!
Giorgio: tutto quello che è stato detto è giusto, io vorrei provare a disegnarlo sganciando tutti i pezzi per vedere cosa viene fuori.
Maestra: Giorgio propone di smontarlo.
(1) Rispetto alla scelta delle creazioni matematiche da discutere la mia collega e io abbiamo predisposto una tabella in modo da tenere traccia dei lavori individuali (creazioni matematiche o testi liberi) discussi collettivamente o revisionati insieme in modo che ogni bambino abbia almeno uno di questi ripreso a grande gruppo.
Commenti D.M.
Dovresti portare in classe un pallone da calcio così vedrebbero che la rotondità (sempre relativa ovviamente) viene fuori dal fatto che non ci sono solo pentagoni ma anche esagoni e poi potrebbero verificare che se mettono vicini solo esagoni si ottiene una tassellazione che ricopre il piano ma non esce dal piano… qui c’è il teorema in atto sulle tassellazioni per cui nei vertici la somma degli angoli è sempre 360° (un angolo giro).
Le tassellazioni servono per farli ragionare sugli angoli che poi però andrebbero tolti dai poligoni e presi come oggetti a se stanti per coglierne tutte le caratteristiche e ragionare sulle semirette che si incontrano in un punto.
Con questa attività, in un percorso a ritroso, si arriva agli enti primitivi (punto, retta, piano) e a capire che l’angolo non lo è, ha bisogno del piano e della retta per costituirsi come ente geometrico.


















