Francesca Demartini, classe prima, Pinerolo (TO)
Quest’anno anche io sono in una classe prima, con 17 alunni. In questi mesi abbiamo lavorato molto sul calendario che ci ha aperto molte occasioni di conteggio: contiamo i bambini assenti e presenti, i giorni che mancano ad una specifica data, alla fine di ogni mese abbiamo contato i giorni di scuola per poi confrontarli con i giorni in cui siamo stati a casa.
Il materiale che riporto non è molto e riguarda solo una parte degli alunni.
Abbiamo poi portato avanti alcune discussioni e attività di conteggio:
– Dove sono i numeri?
– Che cosa si può contare
– Attività di conteggio e segnatura
Ho detto ai bambini di contare i pennarelli presenti nel proprio portapenne e di rappresentare la quantità contata sul foglio, al fine di poter avere sempre il foglietto come riferimento e controllare qualora si perdessero dei colori. La maggior parte rappresenta il pennarello disegnandolo piuttosto fedelmente, alcuni si avviano verso strategie più economiche che però rimangono ancora ancorate alla forma dell’oggetto contato: linee e pallini allungati.
La donnina che contava gli starnuti
Al rientro dalle vacanze ho ripreso il lavoro sulle segnature e l’ho portato avanti proponendo il racconto della Donnina che contava gli starnuti (G. Rodari). Mi sono accorta del fatto che la maggior parte degli alunni tende a scrivere direttamente il numero degli oggetti contati, questa viene considerata, dai più, la strategia più veloce ed efficace per determinare la quantità di oggetti contati. La storia della donnina ci ha dato la possibilità di parlare dello zero ma anche di aprire il discorso sul confronto di quantità riflettendo sul chi avesse fatto più starnuti e perché.







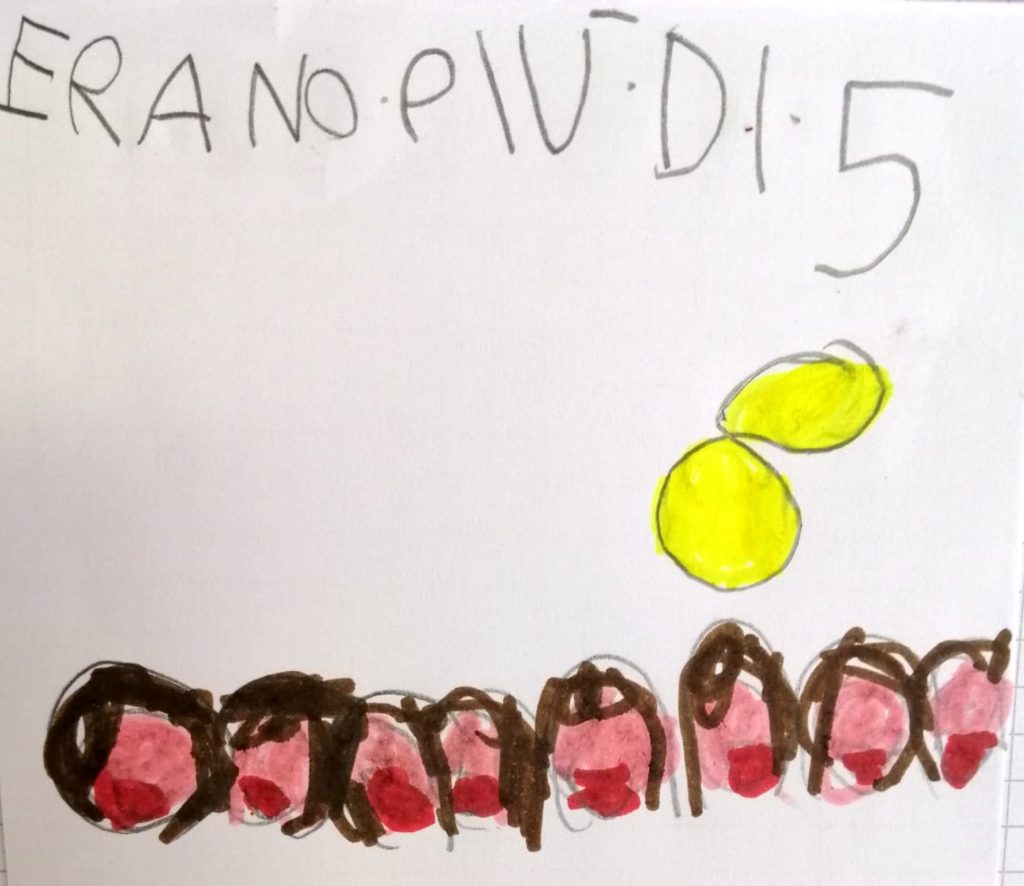




Contare per…






Dalla discussione è emersa l’importanza del raggruppare per… al fine di contare più velocemente le quantità.
L’idea di raggruppare per 2, 3 ,4 ,5 e poi per 10 è emersa in modo davvero spontaneo. Una volta che Emma ha proposto di raggruppare per 2 al fine di contare più velocemente, tutto il resto è venuto da sé.
Un nodo cruciale sarà comprendere il significato della cifra usata per indicare il numero di righe da 10. Credo che usare la frase “2 volte dieci” (ad esempio) possa aiutarli a capire bene il significato sotteso. Il passaggio successivo potrebbe essere dargli un numero e farli ragionare su quanti gruppetti da 10 si riescono a creare. Prima fare tante attività con la manipolazione di materiale, costruire concretamente i gruppi da 10 e contare per 10, per poi passare alla sola dicitura orale.
Le creazioni matematiche
Le creazioni matematiche realizzate
La creazione di Emma
Oggi abbiamo discusso la creazione di Emma. È già un po’ venuta fuori l’idea che contare la polenta non è come contare le cannucce ma ho cercato di soffermare la loro attenzione sulla successione dei numeri scritti dalla bambina. Non è emersa in modo molto chiaro la regola del +1, loro dicono “bisogna scrivere i numeri in ordine, uno dopo l’altro” credo che in questo “uno dopo l’altro” loro intendano quel +1. Osservando la successione i bambini hanno detto che i numeri erano scritti troppo appiccicati e ci si poteva facilmente confondere. Una bimba dice: “Se leggo 1 e 2 vicini può essere anche 12 ma il 2 è anche molto attaccato al 3 quindi potrei leggere anche 23.” È emersa l’esigenza di lasciare dello spazio tra un numero e l’altro per poter capire meglio e poter leggere bene la sequenza.
Attività di conteggio a coppie
16 febbraio – La linea dei numeri

21 febbraio – Conteggio dei fagioli

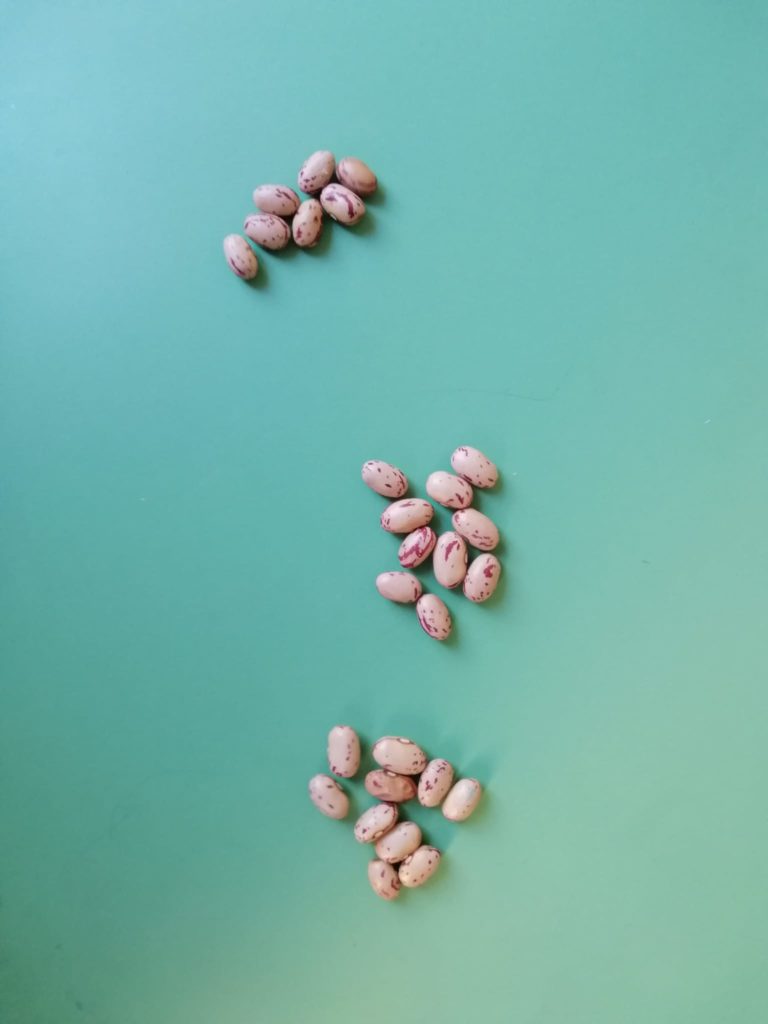
2 marzo – La posizione delle cifre
Leggiamo la lettera inviata dagli alunni di Barzago della classe di Irene e avviamo una discussione.







4 marzo – Decine e unità
Il lavoro su decine e unità è continuato contando diversi tipi di materiali, soprattutto cannucce che ci permettono di creare facilmente gruppi da 10 utilizzando degli elastici. Attraverso la scatola delle decine e delle unità abbiamo ripreso concetti emersi nelle discussioni nei mesi precedenti. Gli alunni si erano già accorti del fatto che in un numero la cifra a destra indica i pezzi singoli, da soli, le unità, mentre la cifra a sinistra indica i gruppi da 10, quindi le decine. Sulla base di queste affermazioni abbiamo deciso di rendere fisse le due scatole: decine e unità, in modo da non confonderci più. La riflessione sulle scatole è poi continuata con lo scopo di capire quante fossero le cifre che si possono mettere in ciascuna scatola, quanto e perché deve avvenire il cambio.
Scrivendo e rappresentando diversi numeri utilizzando le scatole, siamo giunti ad un punto cruciale. 99 lo sappiamo scrivere e rappresentare ma se aggiungo uno in più cosa succede?


Commento D. Merlo
Nella discussione nasce già l’esigenza del secondo raggruppamento quello da 10 decine cioè il centinaio. I bambù i sanno come si scrive 100 e da questo deducono che serva una terza scatola. Questo aspetti dei gruppi d gruppi è ancora da condividere, è un passaggio delicato e non tutti ci arrivano subito. Per ora sanno che si può andare avanti aggiungendo scatole a sinistra (perché non farlo?) e che lo zero in questi caso ha la funzione di segnaposto. Se faranno esperienze con i contatori si accorgeranno però che in questi strumenti anche gli zeri davanti hanno una funzione… e che quindi 07 = 7 mentre 70 ≠ 07. Sarebbe utile introdurre la pascalina per far vedere come e quando avviene al cambio di decina e poi al cambio di centinaio.

Su questa macchina però si può fare un lavoro più dettagliato in seconda con l’attività “Pascal ci insegna a contare”.
Riprenderei però i mazzetti di cannucce per far vedere che c’è la regola del 10 anche con i mazzetti e c’è anche un cambio di nome. In seconda si approfondirà ma intanto sanno già contare per dieci e quindi arrivare almeno al cento si può fare.
Addizioni e sottrazioni
Rispetto ad addizioni e sottrazioni siamo partiti dalla linea dei numeri realizzata con i bicchieri e con i fagioli grazie alla quale i bambini avevano scoperto la regola del +1 e del -1. Da quel momento gli alunni hanno iniziato a voler mettere insieme quantità diverse e provare a togliere quantità differenti partendo da un numero da loro individuato.
Abbiamo realizzato una scatola con due fori per inserire quantità diverse e far scoprire ai bambini cosa accadeva. La scatola ha subito suscitato l’interesse di tutti.



Dopo aver compreso bene il funzionamento della macchina per le addizioni, alcuni bambini hanno voluto provare a realizzare una macchina per le sottrazioni. Ma come realizzarla?
Ho raccolto le ipotesi dei bambini.
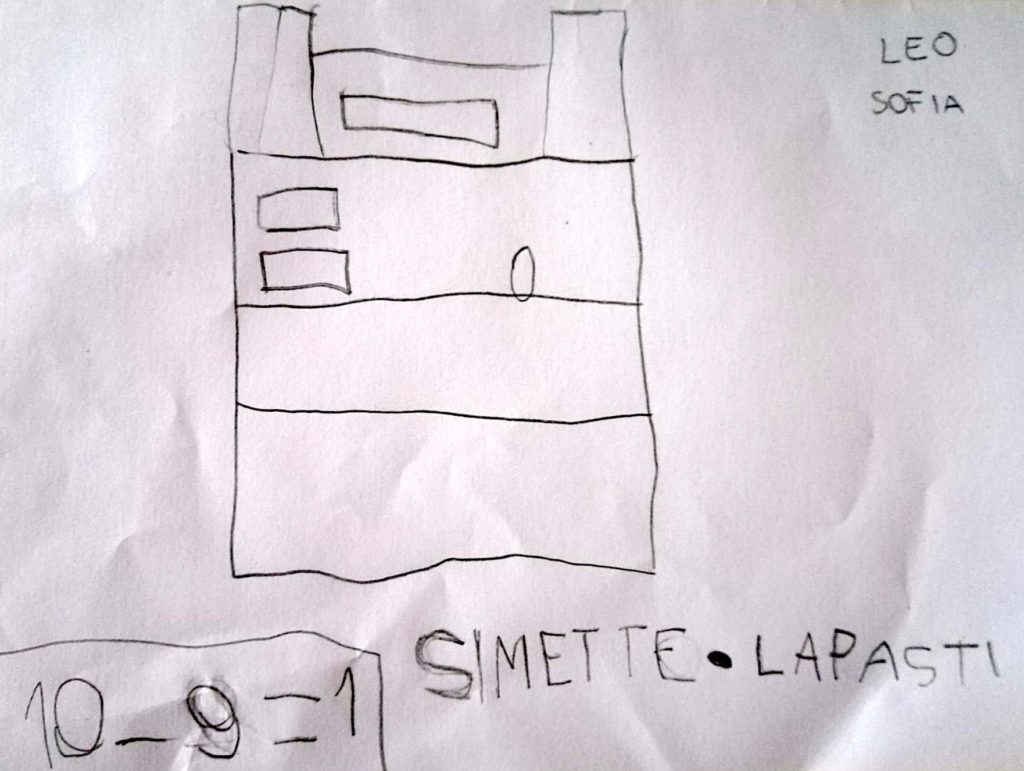

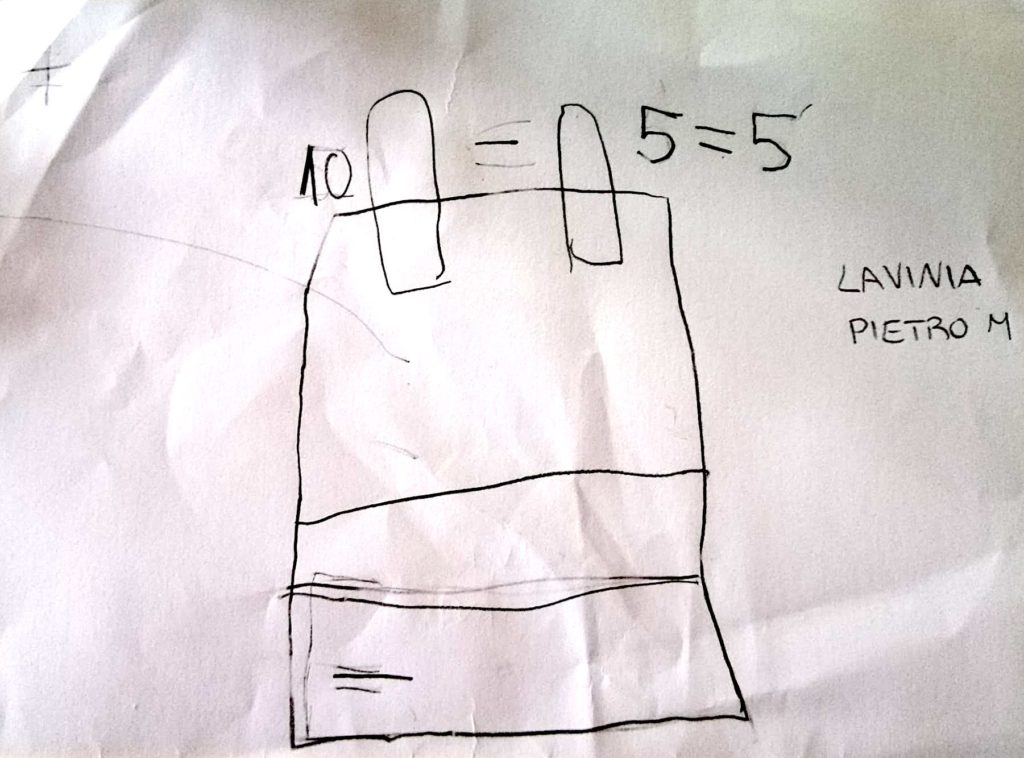
Poi ho portato a scuola un contenitore forato e delle palline riprendendo il lavoro di Luisella e Anna in merito a questo tema. I bambini hanno osservato il contenitore, provato ad utilizzarlo e iniziato a fare le loro ipotesi rispetto al suo funzionamento.





Commento di D.Merlo
Ci sono alcuni punti notevoli nel filmato che vorrei sottolineare:
a) il linguaggio: le palline che cadono sono quelle “tolte” dalla macchina, quindi si stimolano i bambini a rielaborare il modello intuitivo del “togliere” per comprendere che cosa fa la macchina e adattarlo a questa nuova situazione;
b) le dita per contare: si vede che quando devono dire quante sono in tutto le palline addizionano le piccole e con le grandi e usano le dita anche se non in modo appariscente; questo potrebbe essere uno spunto per far dire come si fa a contare 5+4 e quindi cominciare a tenere a mente il primo numero (se non ancora stato fatto);
c) le terne additive: tutta l’attività suggerisce che il numero maggiore, quello del totale delle palline, è in realtà composto di due parti, quelle che vengono addizionate quindi 9 = 5+4 è un fatto additivo che con la sottrazione può diventare 9 – 5 = 4 ma anche 9 – 4 = 5. Su questo si potrebbe cominciare a lavorare con la strategia dei number bonds cioè trasformare ogni addizione in due sottrazioni (l’addizione è commutativa quindi in realtà è anche 9 = 4 + 5). S tratta di puro esercizio che però aiuta a vedere come l’addizione e la sottrazione siano legate tra loro.
Conteggio nel discreto e nel continuo
Contando diverse tipologie di materiali discreto abbiamo realizzato due cartelloni per allenarci a contare per 2 e per 10 al fine di rendere più veloce il conteggio e fare in modo che tutti i bambini sperimentassero queste due strategie di conteggio veloce da loro individuate già nei primi mesi di scuola.


Per quanto riguarda la differenza tra contare nel continuo e nel discreto vorrei partire dalla discussione di alcune creazioni da loro realizzate



in particolare le creazioni di: Kevin, Francesco e Pietro M. per passare poi alla manipolazione di materiali continui come polenta, acqua, farina e vedere quali strategie di conteggio riescono ad individuare con le relative problematiche che potrebbero emergere e diventare spunti per nuove riflessioni.
Commento di D. Merlo
Il fatto che nelle creazioni siano presenti contemporaneamente materiali dei due tipi dovrebbe facilitare il confronto. Si potrebbe partire dal differente modo di manipolarli sperimentato durante la produzione della creazione:; come avete fatto per realizzare questa creazione? Che differenza c’era tra usare la polenta e usare i fagioli? Se qualcuno volesse fare una creazione uguale alla vostra come potrebbe fare? Quanti fagioli, cotton fioc, cannucce, pasta… avete usato? E quanta polenta? Come fare per dirlo?















