Il 3 e il 4 dicembre 2025 presso l’Università della Valle d’Aosta si è tenuto il convegno SeMa Sensing Mathematics for inclusion con l’intento di creare un dialogo tra la pedagogia speciale e la didattica della matematica.


Durante la plenaria del 3 dicembre si sono alternate le voci di professori e ricercatori con l’obiettivo di sensibilizzare la scuola a “vedere” gli alunni con bisogni educativi speciali all’interno del processo di insegnamento – apprendimento. Riportiamo alcune note relative agli interventi che siamo riuscite a seguire, non avendo potuto essere presenti fin dall’inizio.
La docente Elisabetta Robotti, dell’università di Genova, ha invitato i docenti di tutti gli ordini e gradi scolastici ad usare strumenti concreti con gli alunni nell’apprendimento della matematica, al fine di aiutare questi ultimi a costruire ragionamenti che li portino alla risoluzione di situazioni matematiche non banali.
La dottoressa Francesca Gregorio, dell’HEP Vaud di Losanna, ha confrontato il modello scolastico del Cantone di Vaud, in Svizzera, con il modello Italiano. In Svizzera sono ancora presenti scuole speciali per gli studenti con bisogni educativi speciali, ciò comporta il fatto che nella maggior parte delle scuole del Canton di Vaud sia molto basso il numero di alunni BES nelle scuole non speciali. La dottoressa ha poi presentato le modalità attraverso le quali un bambino o una bambina viene diagnosticata con discalculia dai neuropsichiatri infantili. I bambini vengono sottoposti a test aritmetici in particolare di calcolo a seguito dei quali viene redatta una diagnosi che però non tiene per nulla conto delle capacità e delle competenze del soggetto in altre aree matematiche come ad esempio quella del saper ragionare e argomentare. Questo aspetto è stato occasione di confronto tra i presenti, ha aperto ragionamenti sui punti di forza e di debolezza delle diagnosi di discalculia e sulla necessità di creare occasioni di dialogo e confronto anche con il ramo sanitario. La dottoressa Gregorio ha poi presentato il lavoro portato avanti con una studentessa di scuola secondaria di primo grado con difficoltà nell’ambito matematico a cui era stato sottoposto un item algebrico. L’alunna in questione, con le giuste stimolazioni è riuscita ad articolare un buon ragionamento per arrivare alla soluzione corretta dell’item pur non avendo mai studiato algebra negli anni precedenti.
La notazione utilizzata da quest’alunna è la seguente:

da aritmetica è diventata “algebrica” quando ha colto la regolarità, ha quindi abbandonato i numeri e li ha sostituiti con dei tondini:
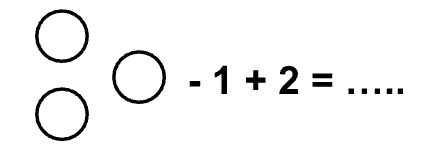
(il tondino sta al posto del numero di quadrati che si vogliono ottenere).
La dottoressa ha poi terminato il suo intervento con una provocazione: è quindi giusto esonerare completamente un alunno dallo studio di alcuni aspetti della matematica perché reputati troppo complessi o siamo noi che ci poniamo dei limiti laddove il ragionamento di un alunno potrebbe non averne?
Tra gli interventi che ci hanno colpite spicca una proposta che ormai fa parte del repertorio del nostro gruppo di ricerca, la creazione di un pattern e la ricerca della regola con cui è costruito. Il pattern proposto, da realizzare con materiali concreti, le cannucce, è il seguente:
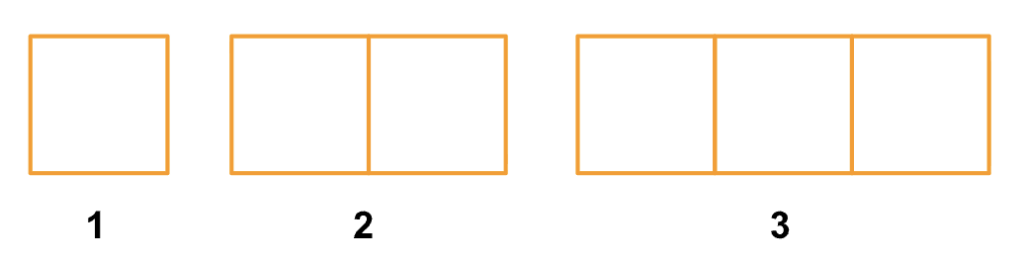
Quante cannucce per la 4° posizione? E per la 100°? Qual è la regola?
| quadrati | cannucce |
| 1 | 4 |
| 2 | 7 |
| 3 | 10 |
| 4 | …. |
| 5 | …. |
Nella seconda parte della giornata i docenti Bellacicco, Capone, Casi e Soldano hanno presentato il progetto AB MOVE! facendo sperimentare ai docenti presenti la positività didattica delle pause attive.
Infine, i docenti Manolino, Bernareggi e Maffia hanno presentato, sempre in plenaria, la necessità di andare oltre l’accessibilità comunemente intesa in matematica per studenti con disabilità sensoriali. Per rendere accessibili agli alunni ciechi o ipovedenti i calcoli in colonna o la risoluzione di equazioni di secondo grado, si prevede l’uso di strumenti che invece di aiutare l’alunno nella risoluzione di un quesito affaticano e aumentano il carico cognitivo.
Usare uno strumento per ingrandire un’equazione di secondo grado, utilizzare il sintetizzatore vocale o dare l’opportunità di usare il cubaritmo per risolvere un calcolo in colonna rende sì accessibile il quesito allo studente con disabilità sensoriale, ma siamo sicuri che l’accessibilità all’item corrisponda ad una reale pratica didattica inclusiva laddove l’uso dello strumento sovraccarica piuttosto che semplificare? Questo non significa che agli studenti ciechi non si debbano insegnare i calcoli in colonna oppure la risoluzione di equazioni di secondo grado, significa provare a cercare strade alternative che coinvolgano direttamente persone e alunni con disabilità sensoriali per capire insieme quale percorso intraprendere per rendere non solo accessibile ma davvero inclusivo il percorso di apprendimento della matematica anche in presenza di queste disabilità.
I materiali relativi a questi interventi saranno disponibili sul sito dell’università https://www.univda.it/eventi-univda/sema-for-inclusion-sensing-mathematics-un-dialogo-tra-pedagogia-speciale-e-didattica-della-matematica/
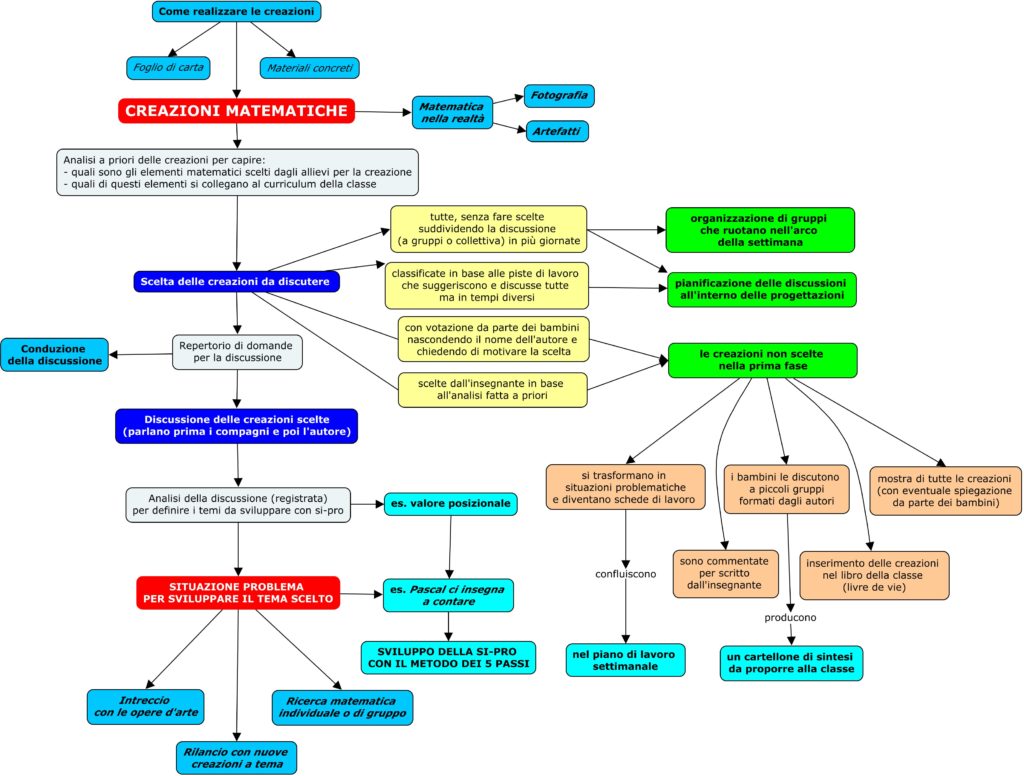
Il laboratorio Creazioni matematiche: fare, pensare,condividere.




Dopo un breve momento di accoglienza dei partecipanti, l’attività è iniziata con la discussione su «Che cosa è una creazione? E una creazione matematica?»

I partecipanti – 9 di cui 2 insegnanti in servizio, una della scuola dell’infanzia e una della scuola primaria, e 7 studentesse di Scienze della Formazione Primaria, alcune già con incarichi nella scuola – hanno prodotto le loro creazioni utilizzando, per nostra scelta, solo fogli bianchi formato A4 e matite o pennarelli.

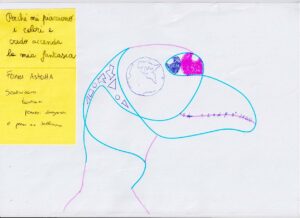
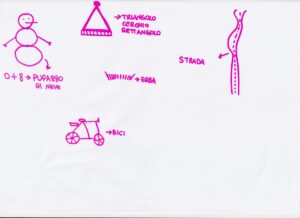
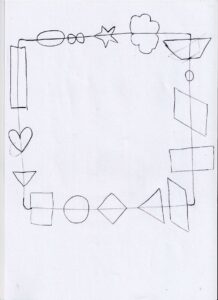


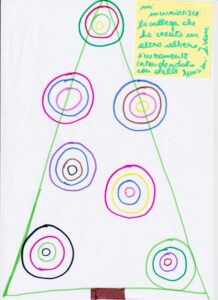


Dopo il momento della creazione abbiamo esposto tutti i lavori e chiesto di scegliere una sola creazione scrivendo su un post-it perché l’avevano scelta. Non tutte sono state scelte: Doc. 1, 5 e 6 sono state scelte da due persone, dovendo poi sceglierne una tutti hanno optato per il Doc. 6.
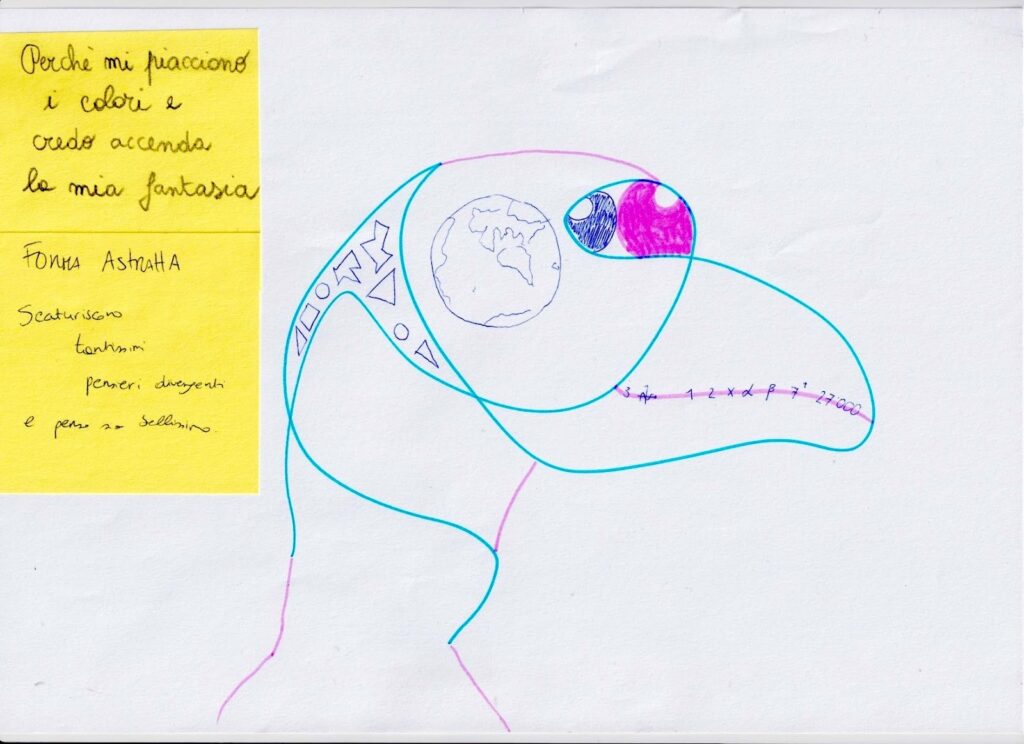
La forma suggeriva per alcuni un uccello, altri invece si sono soffermati sull’intreccio delle linee, interessanti da analizzare dal punto di vista topologico per la continuità e le connessioni. Gli elementi più “matematici” erano le forme e i simboli matematici presenti nel “becco”, ma, in contrasto con le nostre aspettative, la discussione non si è sviluppata a partire da questi elementi; hanno attirato maggiormente l’attenzione il mondo e l’“occhio” con le due “pupille” colorate. Come è scritto su un post-it, dall’osservazione “scaturiscono tantissimi pensieri divergenti”, è una figura che “accende la fantasia”.


In seguito alla discussione, che si è accesa intorno alle creazioni adulte dei partecipanti, ci è sembrato importante mostrare una scelta di creazioni di alunni di scuola dell’infanzia e primaria realizzate nelle classi degli insegnanti del nostro gruppo di ricerca.
Abbiamo privilegiato la scelta di creazioni da cui si fosse sviluppato un percorso per condurre gli alunni a costruire nuove conoscenze matematiche, coerenti con il curricolo della classe. Per ogni esperienza abbiamo sintetizzato il percorso elencandone i punti salienti.
Ad esempio per l’esperienza riferita alla scuola dell’infanzia e intitolata Giochiamo con i pattern il percorso che si è sviluppato a partire da questa creazione realizzata con materiali poveri:

Il percorso seguito dall’insegnante è così sintetizzabile:
- Lista e conteggio dei materiali utilizzati nella creazione.
- Rappresentazione grafica della creazione.
- Pista di lavoro: i pattern algebrici – con riferimento alle Indicazioni Nazionali: “Il bambino raggruppa e ordina oggetti e materiali secondo criteri diversi, ne identifica alcune proprietà (…) utilizza simboli per registrarle (…)”.
- Rappresentazione dei “fiori” utilizzando tappi e cannucce: si parte con un tappo e 4 cannucce, come si prosegue?
- E se partissi con un tappo e 5 cannucce, come si potrebbe proseguire? Che cosa cambia e che cosa resta uguale dopo ogni passaggio?
- Proposta di una nuova situazione problematica: trovare la regola per continuare l’albero di mattoncini illustrato in figura:

Successivamente sono stati presentati altri quattro percorsi visibili direttamente sul sito del gruppo:
Da una piramide di bicchieri (classe prima)
Braccialetti matematici (classe prima)
Geometria in arte (classe terza)
La creazione di Aya (classe quinta)
I feedback dei partecipanti al termine dell’attività sono stati interessanti: dimostrano come, allo spiazzamento iniziale, sia seguito un grande coinvolgimento nella ricerca comune dei significati matematici, e, forse, un desiderio di applicare quanto sperimentato nelle loro classi presenti e future.


Bibliografia e sitografia di riferimento per il laboratorio
Aiolfi, A., Cometto, A., Merlo, D., Vio, E., (2024). Il senso del misurare. Laboratori dai 3 ai 14 anni, Roma, Carocci editore.
Arzarello, F. (a cura di), (2024). Matematica come discorso. Esperienze in classe dalla primaria alla secondaria. Milano, UTET Università.
Le Bohec, P. (2020). Il testo libero di matematica, eBook Edizioni MCE
Merlo, D., Cometto, A. (2025). Moltiplicare e dividere. Laboratori e percorsi didattici per la scuola primaria, Roma, Carocci editore.
Link alle slide del laboratorio Creazioni matematiche: fare, pensare, condividere.
Sito “Creazioni matematiche”: https://creazionimatematiche.mce-fimem.it/
Sito MCE: http://www.mce-fimem.it/
Alcuni riferimenti dati dai relatori
Croset&Gardes (2022), The impact of the Montessori Education on early number learning in French pre-schools, PDF.
Garzetti, M. (2024), La didattica a stazioni per la differenziazione didattica, Slide scuola estiva UMI 2024.
Shapiro, L. (2019), Embodied cognition, London, Ed. Routledge.
Bruner, J. S., (1973), Il significato dell’educazione, Roma, Armando.
Materiali
Sito Polypad con manipolatori virtuali.