Alice Marazzina, classe seconda, Milano








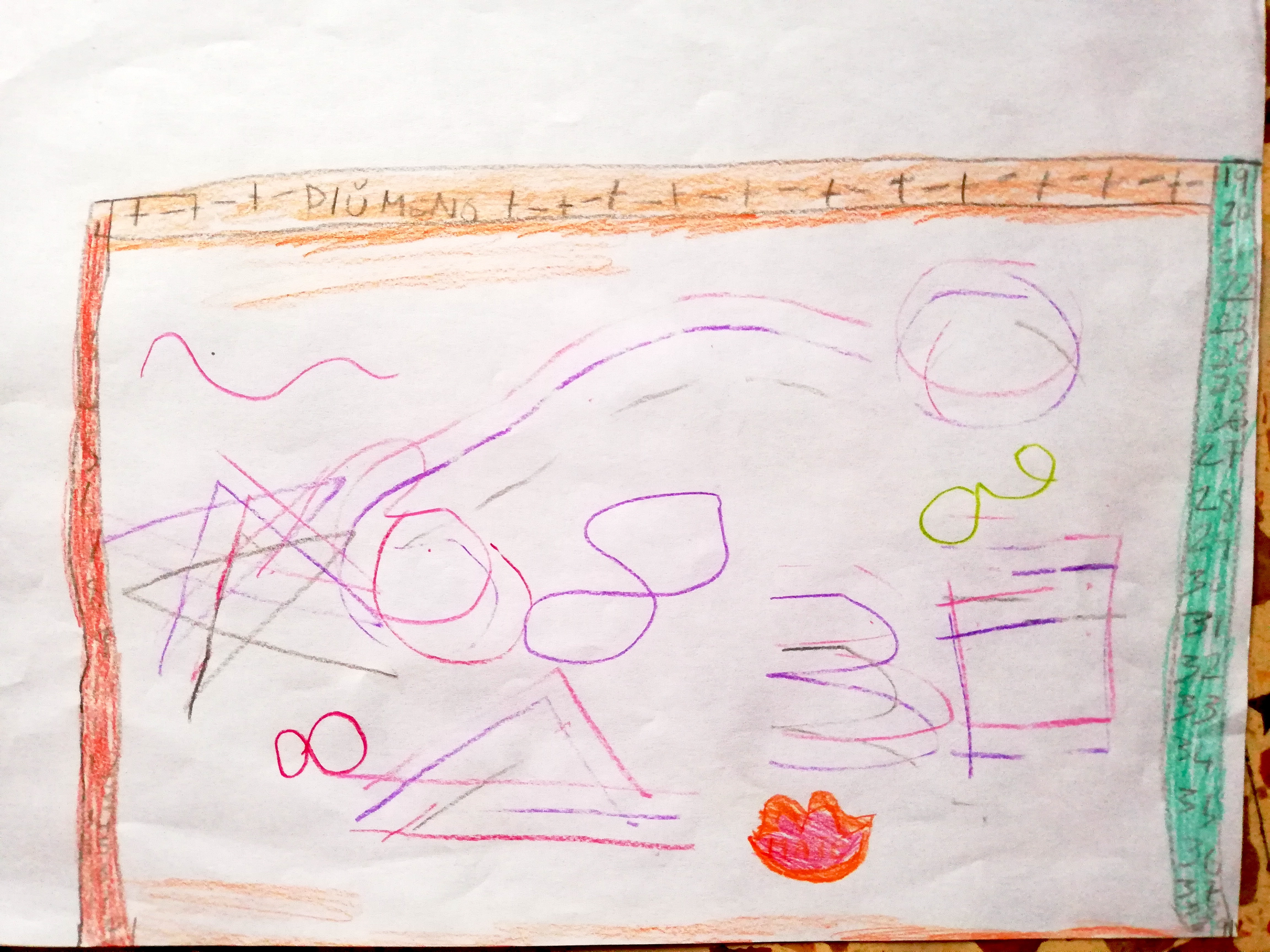
La discussione delle creazioni
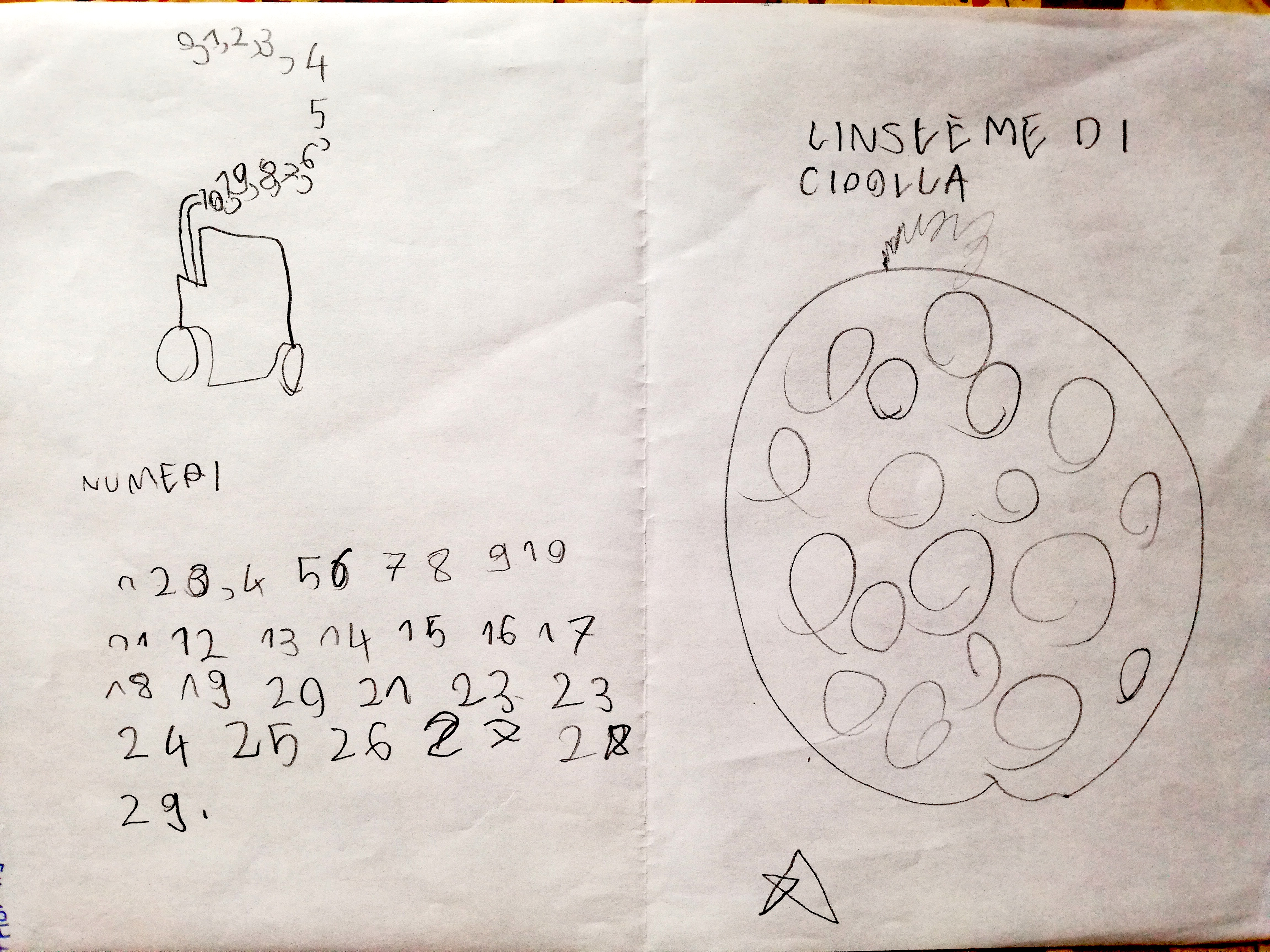
Discutiamo la creazione matematica di Anna
Le creazioni da discutere sono state scelte dell’insegnante.
L’insegnante riporta alla lavagna solo la prima parte della creazione, fino al numero 53. Quindi la discussione riguarda la parte alta della creazione.
Legenda: I = insegnante

ALICE: ci sono tanti numeri
I: tanti numeri. Quali?
ALICE: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42 ,43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53.
I: ok, per dirlo più velocemente, possiamo dire che ci sono i numeri da…
ARJUN: da 1 a 53
I: quindi sono in ordine, giusto? Che ordine c’è?
ALICE: sono tutti in fila
I: sono tutti in fila e vanno…
ALICE: d’accordo
ARJUN: questo (indica la terza linea, quella spezzata) sembra l’erba, questo (indica la seconda linea) sembra il mare, questo sembra il cielo (indica la prima linea orizzontale)
CRI: questo qua (indica un pezzetto di linea curva) sembra un po’ un trattore
THOMAS: dal 3 fino al 13 sembra un mare
MANJOT: da qua a qua (indica linea dal 14 al 27) sembrano delle onde sonore
MARIASOLE: dal 14 al 27 sembrano le montagne
I: ora, invece di concentrarci su cosa sembra, concentriamoci per capire quale matematica ha messo Anna in questo disegno. Quindi quello di matematica che vedete.
LISA: le linee
I: le linee, ad esempio, quale linee ha usato Anna?
LISA: le linee spezzate
I: sì, ci sono delle linee spezzate per esempio queste qui che sembravano delle montagne o dell’erba
LISA: linee arrotondate
I: queste linee un po’ arrotondate come si chiamano?
CRI: curve
LISA: linee miste
I: alcune sono delle linee miste, bravissima. Questa qui comincia curva ma poi si rompe e diventa spezzata
ARJUN: poi qua di nuovo fa una curva
I: chi si ricorda come si chiama questa linea qua (indica la linea di fianco al sole)?
GABRI: linea orizzontale
I: è una linea orizzontale
CRI: ci sono delle “l” in corsivo in questa linea (indica parte della linea curva)
I: alcune sembrano delle lettere fatte in corsivo
JAPLEEN: quella linea che è dritta possiamo anche dire che è retta (si riferisce alla prima linea senza numeri di fianco al sole)
I: è una linea retta, bravissima. Le linee che vanno dritte così… Gabriele stai attento che Japleen ha detto una cosa in più rispetto a quello che hai detto tu, questa linea orizzontale è anche una linea retta perché va tutta dritta. È retta e orizzontale.
CRI: questa sembra una “m” in corsivo (indica parte della linea curva)
I: ok, in queste lettere che vede Cristalina cos’altro c’è? Sembrano delle lettere…. quando la linea si sovrappone cosa si forma?
ALICE: incroci
I: un incrocio, perfetto
MANJOT: come un incrocio stradale
LISA: oppure qua (indica un incrocio di linee)
CRI: qui, qui (indica incroci di linee)
I: perfetto, ce ne sono tanti.
CRI: Poi, sempre sulle linee, c’è questa che è un tipo di linea (indica il sole) mentre questa è un altro tipo (indica la linea da 14 a 27) …
GABRI: linea chiusa e aperta
I: questa è una linea chiusa e Anna l’ha usata per fare una specie di sole mentre questa (indica la linea da 14 a 27) è una linea aperta
CRI: questa è aperta (indica una linea)
I: vi viene in mente qualcos’altro?
ALICE: anche questa è aperta
LISA: ha messo la creatività perché con le linee ha fatto il mare, le montagne, il sole
I: è stata molto creativa Anna, è vero. Con le linee ha fatto tante cose
JAPLEEN: il sole è fatto con una linea chiusa
I: il sole è fatto con una linea chiusa e curva, esatto. Invece i raggi intorno sono fatti con una linea spezzata e chiusa
I: c’è altro o facciamo parlare Anna?
THOMAS: basta
I: Anna vieni a presentare il tuo disegno.
Faccio vedere, prima di tutto, il disegno originale agli altri. Queste cose che hanno detto loro le avevi pensate tutte…. qualcuna di più, qualcuna di meno? ANNA: quasi
I: Quasi tutte. Loro ne hanno pensate di più o di meno di te?
ANNA: di più
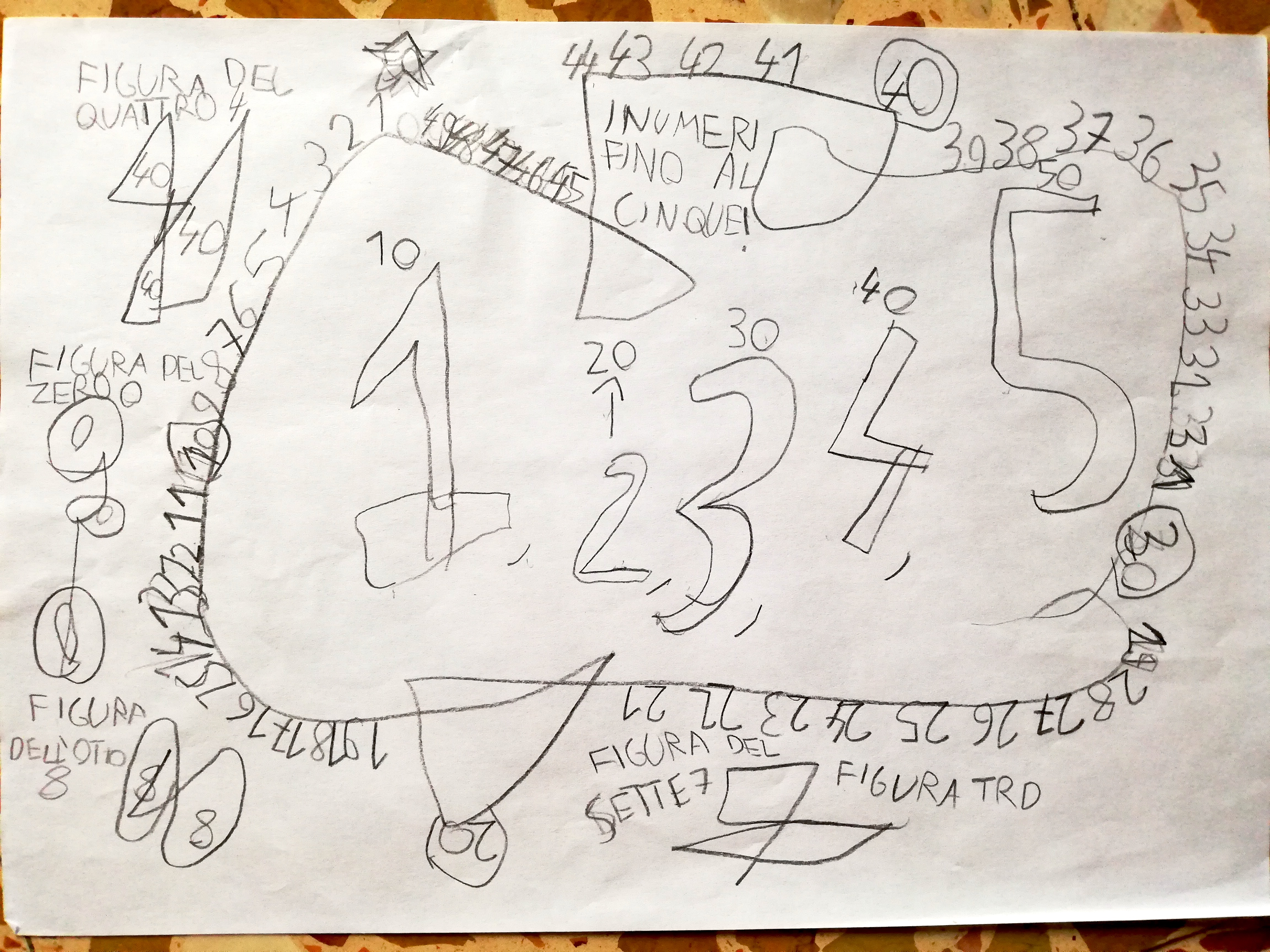
I: allora è stato utile sentire quello che ti hanno detto. E tu hai fatto un bellissimo disegno perché era ricco di tante cose. I numeri? Che numeri hai scelto? Come hai fatto a sceglierli?
ANNA: li ho fatti in ordine
I: ok quindi dall’1 fino al 53. Invece raccontaci come hai fatto la parte finale, quella che io non ho disegnato alla lavagna?
ANNA: ho fatto un cuore con l’addizione, una stella con l’addizione e delle barche.
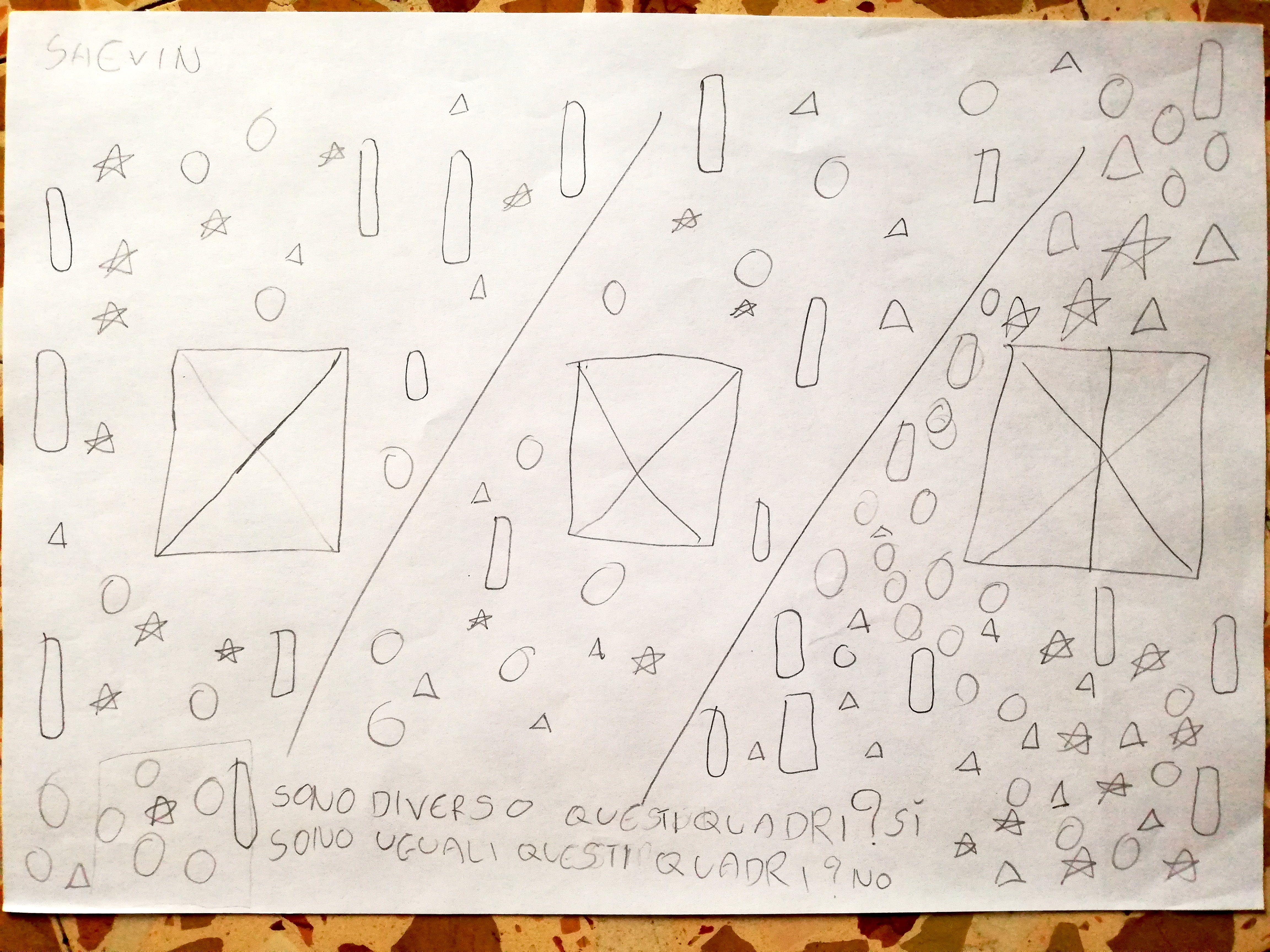
Discutiamo la creazione matematica di Arjun

I: abbiamo il disegno che ha fatto Arjun… più o meno. Ho cercato di farlo il più simile possibile. Visto che è quello di Arjun, possono parlare tutti i bimbi tranne Arjun.
I bimbi guardano e provano a dire che tipo di matematica c’è nel disegno di Arjun.
JAPLEEN: il per (x)
I: sì, qui (indica la x) vediamo il per. Che cos’è il per?
JAPLEEN: è la moltiplicazione
I: è la moltiplicazione, quindi è il segno di un’operazione. Cristalina tu cos’hai visto?
CRI: ci sono tante forme
THOMAS: sembra un trattore
I: dove lo vedi il trattore?
THOMAS: (indica tutta la lavagna) e c’è un tubo
I: ah, tu dici che tutto questo è un trattore
GABRI: a me non sembra un trattore
MANJOT: qua (indica una forma) sembra una bandierina di un compleanno. Poi c’è anche il meno e il più
I: oltre al x, c’è anche il – e il +
INGRID: ci sono i numeri
CRI: ma che cos’è questo?
I: poi lo chiediamo ad Arjun
CRI: ci sono tre punti esclamativi e tre punti di domanda
I: e, secondo te, i punti di domanda c’entrano con la matematica?
CRI: si, quando magari facciamo gli insiemi….
I: a chi viene in mente quando incontriamo i punti di domanda?
LISA: quando facciamo un problema, c’è la domanda e mettiamo un punto di domanda
I: giusto. Qualcos’altro su questo disegno?
Ad esempio, abbiamo detto che ci sono i numeri. Che tipo di numeri ci sono?
JASMEEN: 8, 30, 9, 3, 8, 80, 89, 31, 2, 90
I: secondo te, ha messo questi numeri a caso o li ha scelti per qualche motivo?
JAPLEEN: a caso
I: li ha messi a caso, ok. Vi viene in mente qualcos’altro?
THOMAS: ci sono delle ruote
I: si, tu dicevi che questo era un trattore quindi ci sono le ruote, il tubo e il carro
JAPLEEN: sembra un rinoceronte
I: può sembrare un rinoceronte per questa forma (indica triangolo)
CRI: anche sembra un elefante
I: perché un elefante?
CRI: perché c’è questo (indica il tubo)
I: quella per te è la proboscide dell’elefante
INGRID: sembra anche un dinosauro
JASMEEN: sembra un elicottero
I: Arjun vieni, ci presenti il tuo disegno.
ARJUN: io non volevo…Thomas ha detto un trattore però io volevo fare una trinciatrice con le forme e non ci sono riuscito
I: no beh… un pochettino sembra. Infatti qualcuno ha visto un trattore che non è molto diverso dalla trinciatrice.
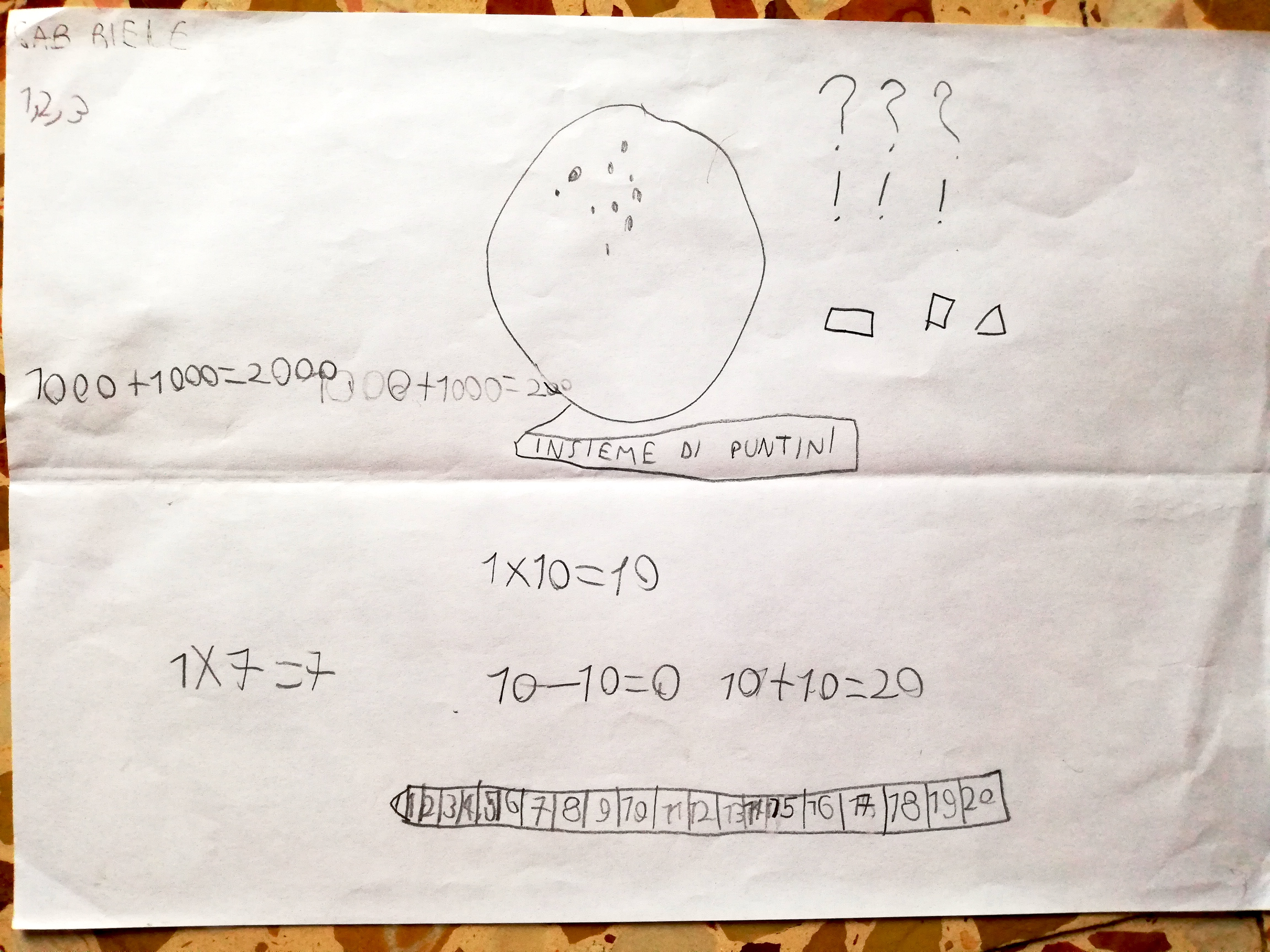
Arjun, vuoi dirci qualcosa dei numeri? Hai messo tutti numeri a caso o qualcuno l’hai scelto?
ARJUN: qualcuno non l’ho messo a caso
I: ad esempio quale?
ARJUN: il 2. Che ho fatto 2+2= 4
I: si, ha fatto un’operazione. Anche qui hai fatto un’operazione 30 + 1, anche qua 9 + 80. Invece forse gli altri numeri li hai messi a caso.
I: Punto esclamativo e punto di domanda perché li hai messi? ARJUN: il punto di domanda, quando facciamo matematica, a volte ci mettiamo il punto di domanda. L’altro così a caso
I: qualcuno ha una domanda per Arjun?
THOMAS: lo so che è una trincia, però sembra anche un trattore.
ALICE: perché c’è il camino?
ARJUN: non mi ricordo… il tubo che usciva il fumo
THOMAS: ah, il tubo di scappamento!
I: quindi hai fatto il tubo di scappamento utilizzando un rettangolo e un triangolo.
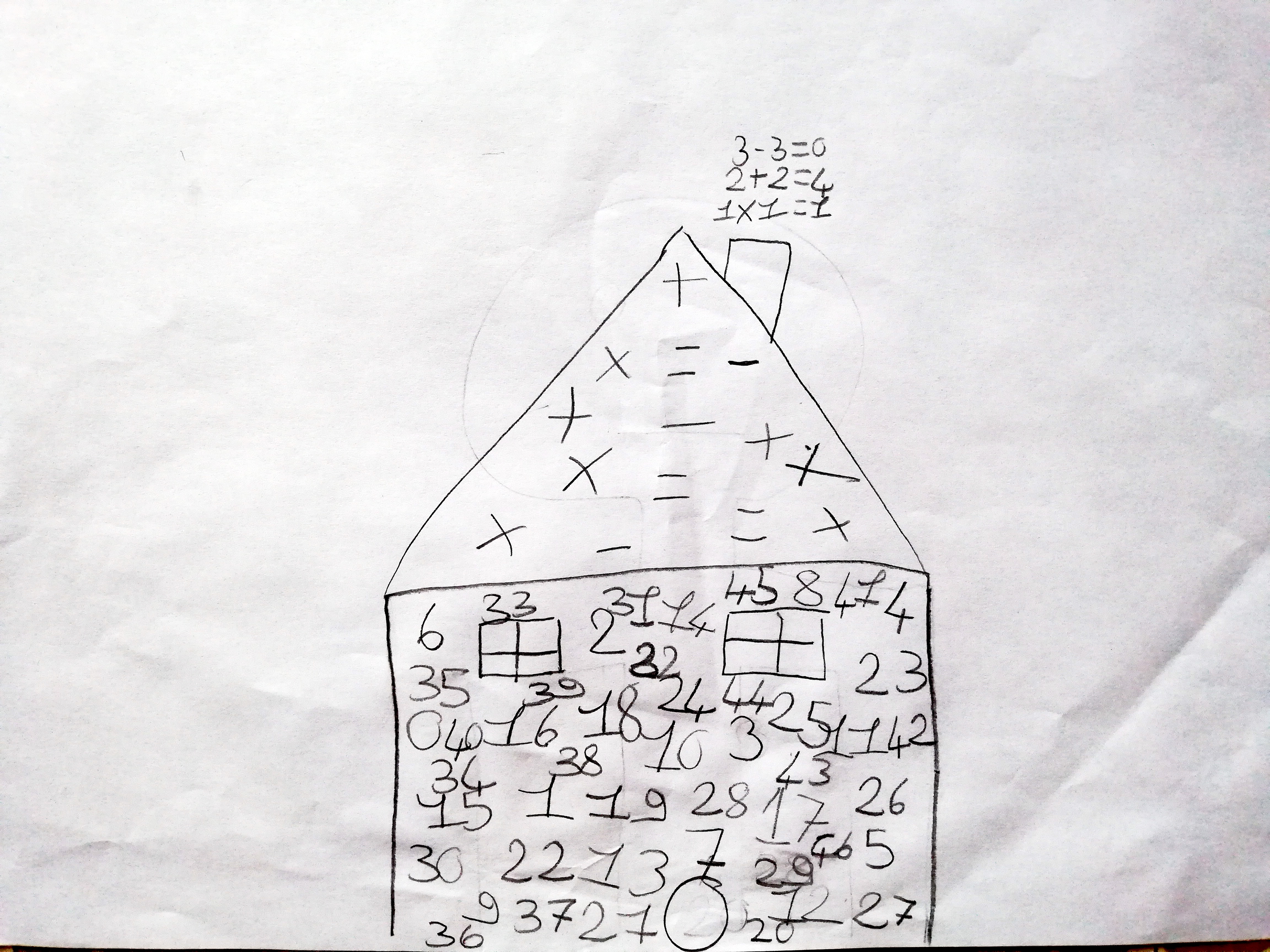
Discutiamo la creazione di Vittoria

I: Questo è il disegno che ha fatto Vittoria quindi parlano tutti tranne Vittoria.
BERIN: questa casa comunque si chiamerebbe “la casa delle operazioni” o “la casa matematica”
I: dopo sentiamo Vittoria quale titolo preferisce
VITTORIA: ma io ce l’ho il titolo!
I: lo puoi dire alla fine. Ci viene in mente qualcosa? Che tipo di matematica ha disegnato Vittoria?
MIRABEL: io ho pensato alla “casa del più e del meno” però c’è anche il per
I: quindi come possiamo chiamarla? La casa del più, del meno…?
MIRABEL: “la casa del più, del meno e del per”
INGRID: però ci sono anche i numeri
I: sì, ci sono anche i numeri
MIRABEL: va beh, va beh, va beh
INGRID : e anche l’uguale
I: è vero, ci sono anche i numeri e anche l’uguale
MIRABEL: sarebbe troppo lungo allora lo lasciamo così (si riferisce al titolo)
I: proviamo a guardare che numeri ci sono, che numeri ha usato Vittoria
BERIN: ha usato 0 4 0, 35, 6, 33, 21, 14, 2, 32, 39, 18, 28. Questo è 15 e 1 o 151?
I: è 15 e 1
BERIN: 15 e 1, 19, 10, 22, 34, 36, 27, 26, 12, 14, 6…
I: ok, perfetto
GIADA: ha usato tutti i numeri
BERIN: i numeri tutti in cifra
I: sono tutti numeri in cifra, non ha usato parole. Giada ha detto che ha usato tutti i numeri e che non ha usato le parole. Cos’altro si può dire di questo disegno?
SHEVIN: da questa parte, sul tetto, ci sono il più, il per, il meno, l’uguale ma non c’è il diviso
I: non ha messo il diviso, vero. Sai come si fa il diviso tu? MIRABEL: io lo so
I: fai vedere come si fa, scrivilo alla lavagna.
BERIN: so anch’io come si fa
KEVIN: anch’io lo so
I: (Shevin è alla lavagna) fai quello che ti ricordi, non importa se è sbagliato. Adesso vediamo come lo fa Shevin se c’è bisogno lo aiutate
MIRABEL: posso farlo io?
I: vediamo Mirabel (Mirabel va alla lavagna)
GIADA: no, non è quello
I: sì, il diviso di può fare così (indica il segno fatto da Mirabel) oppure Giada ha un’altra idea
GIADA: (Giada scrive alla lavagna) oppure così
I: oppure? Qualcuno lo sa fare in un altro modo il diviso?
I: allora il diviso si può fare così o così. Il simbolo che ha fatto Giada si vede molto in giro. È la percentuale. È un po’ difficile da spiegare. Potreste aver sentito 100%… Oppure, in questi giorni nei negozi stanno facendo i saldi i vestiti costa un po’ di meno e nei negozi scrivono – 50%, – 70% . Vuol dire che una maglietta che costa 10 euro con lo sconto del 50%
BERIN: costa 5 euro
I: costa la metà. Costa 5 euro. Comunque è una cosa un po’ difficile che vedremo più avanti
SHEVIN: maestra, anche se c’è il tablet che sta per scaricarsi…prima del…. non mi ricordo bene. C’è la batteria e giù c’è dove è caricato e su c’è dove non è caricato.
GIADA: tipo carica 5%
I: esatto, se c’è scritto carica al 5% vuol dire che ha bisogno di essere caricato
BERIN: 100% vuol dire che non deve essere cariato, puoi toglierlo dalla carica
I: giusto
GIADA: lo sai che il telefono del mio papà è resistito fino all’1% di batteria?
I: sì, dopo l’1% c’è lo 0% quindi vuol dire
BERIN: quindi si spegne e succede che fino a quando non si ricarica non lo puoi usare
GIADA: sì, ha resistito un po’ allo 0 e poi si è spento
I: ok, torniamo a quello che ha detto Shevin. Sul tetto Vittoria ha messo il più, il meno, il per e l’uguale. Volendo, possiamo dire che manca il diviso. Cos’altro possiamo dire?
BERIN: le finestre le ha fatte sembrare un più (+) visto che se guardi bene vedi 5 quadrati o 4 e se guardi bene vedì anche un più (+)
MIRABEL: e se vedi da qua (ruota la testa) c’è anche un per (x)
BERIN: sì, se guardi da qua (ruota la testa) c’è anche un per (x) ma meglio evitare
I: allora, se guardiamo la finestra possiamo vedere 5 o 4 quadrati. Martina, tu quanti ne vedi di quadrati?
MARTINA: 4
I: fammi vedere quali vedi? (alla lavagna indica i 4 quadrati interni) Però puoi vedere anche un quadrato grande intorno. Vero che ce n’è anche uno più grande? Quindi ne abbiamo 1, 2, 3, 4 e 5. E poi queste linee potremmo vederle come un più (+)
JAPLEEN: e un per (x)
I: queste linee, se giriamo la testa, potremmo vederle come per (x). O se immaginiamo di ruotarlo un po’….
GIADA: il titolo della casa potrebbe essere “la casa dei numeri”
I: ok, mancava “la casa dei numeri”. Scriviamo anche questo titolo
MIRABEL: però c’è il +, il – , il x, l’=
BERIN: “la casa delle operazioni” in poche parole
I: ok, qualcos’altro? Abbiamo detto: sul tetto ci sono +, – e x, le finestre sono dei quadrati con dentro il + e il x
GIADA: ecco! La porta sembra uno 0
I: la porta può sembrare uno 0 gigante, sì
MIRABEL: o sta cantando la porta aaaaaaah
I: può essere anche una bocca aperta che canta. C’è qualcos’altro che non abbiamo ancora detto?
MIRABEL: il tetto sembra un triangolo. Il camino sembra un rettangolo. La casa sembra un quadrato.
SHEVIN: no, questa parte non è la casa (indica la facciata)
I: sì, meglio dire che la facciata è un quadrato
KEVIN: ha messo un cerchio qua (indica la porta)
I: guardiamo ai numeri? Li ha messi tutti?
GIADA: no
I: quali ha messo?
MIRABEL: si è dimenticata dell’1
BERIN: ma cosa dell’1 se c’è il 12 e il 10!
MIRABEL: no, intendo l’1, il 2, il 3, il 4, 5, 6, 7, 8, 9, 10
BERIN: ma se ci sono!
I: ok, dopo lo chiediamo a Vittoria. L’ultima cosa che facciamo è scegliere quale titolo è più adatto tra quelli che abbiamo detto
VITTORIA: ma io ce l’ho!
I: sì, però te ne proponiamo uno
KEVIN: secondo me “la casa della matematica”
BERIN: anche per me “la casa della matematica” anche se anche “casa delle operazioni” va bene
I: forse “casa della matematica” è più adatto perché racchiude tutto. Mentre “casa dei numeri” riguarda solo la facciata e “casa delle operazioni” riguarda solo il tetto
MIRABEL: dobbiamo votare?
I: facciamo senza votare perché ormai abbiamo già detto tante cose. Vittoria vieni a presentare
VITTORIA: come titolo anch’io avevo “la casa della matematica”. Poi praticamente questo qui (indica le finestre) volevo fare un quadrato con dentro un +.
BERIN: comunque cosa significa 040?
I: un attimo, tienila lì come domanda
VITTORIA: ho messo tutti i numeri sparsi che mi venivano in mente
I: quindi non hai seguito un ordine
VITTORIA: poi la porta volevo fare un cerchio e dal camino volevo fare uscire delle sottrazioni, delle operazioni così
I: ah, molto bella come idea! Perché tu hai nel tetto i segni, nella facciata i numeri e quindi i numeri uniti ai segni escono dal camino come operazioni. Ora, domanda di Mirabel, cosa vuol dire 040?
MIRABEL: 1400?
VITTORIA: perché semplicemente avevo fatto prima lo 0 e poi il 40. Però gli ho fatti vicini quindi sembra così
I: quindi erano due numeri, lo 0 e il 40. Però sono capitati vicini e noi lo leggiamo 040. Cosa sembra 040?
MIRABEL: 1400?
I: 1400 si scrive così, è diverso
MIRABEL: mille e quattro
I: 040 vi fa venire in mente qualcosa?
BERIN: magari potrebbe dire “ho 4 occhi”. Visto che “ho” c’è questo (indica la o) poi 4 c’è il 4 e “o” che sta ancora per occhi
MIRABEL: siiiii
I: Berin, se tu leggi 040 come “ho 4 occhi” vuol dire che 040 è un codice per dire “ho 4 occhi”
MIRABEL: (indica il 4) ma questo assomiglia a un naso. Degli occhi (si riferisce alle 0) con un naso (si riferisce al 4)
I: assomiglia anche a occhi e naso. Potrebbe essere una faccia
MIRABEL: manca la bocca, i capelli, il cervello.. .
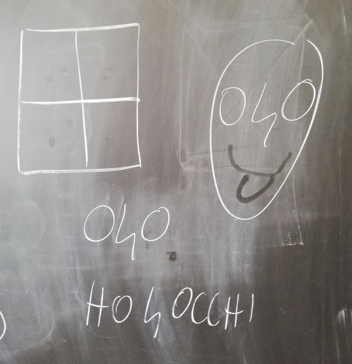
Discutiamo la creazione di Leonardo

I: questo che abbiamo alla lavagna è il disegno, la creazione, di Leonardo. Lui l’ha fatta sul foglio e io l’ho fatta simile alla lavagna. Ora possono parlare tutti i bambini tranne Leo. Noi cerchiamo di capire che tipo di matematica ha messo Leonardo in questo disegno. Chi ha qualche idea la dice. Leonardo parlerà alla fine
BERIN: i numeri dall’ 1 al 10
I: ok, ci sono tutti numeri dall’ 1 al 10
BERIN: a parte 0. Ha messo 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ma non lo 0
I: è vero, lo 0 non c’è. E invece abbiamo visto che anche lo 0 è un numero
KEVIN: ha usato le lettere
I: solo le lettere?
KEVIN: sì
BERIN: no
MIRABEL: ha usato i numeri e le lettere
I: c’è sempre un numero con le lettere. C’è sempre un numero scritto in parola e un numero scritto con i numeri, con le cifre. Quindi c’è sempre parola e cifra, parola e cifra.
GIADA: è in ordine
I: è in ordine?
GIADA: fa una sequenza “parola-cifra, parola-cifra, parola-cifra”
BERIN, KEVIN E ALTRI: è vero!
I: perfetto quindi c’è l’ordine “parola-cifra”…c’è qualche altro tipo di ordine? C’è 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
SHEVIN: perché non abbiamo scritto “cifra-parola” ?
I: qua (indica la lavagna) abbiamo scritto “parola-cifra”
SHEVIN: abbiamo fatto scambio
I: Leo ha disegnato una parola e poi una cifra. Poteva anche scambiarli ma ha fatto parola e poi cifra
BERIN: al massimo perché io gliel’ho consigliato! Perché io gli ho consigliato di mettere “uno” poi però gli ho detto di mettere anche l’ 1 in cifra
I: ok, vi viene in mente qualcos’altro?
GIADA: dal minore al maggiore
I: dal minore al maggiore, sì. Spiega meglio
GIADA: dal numero più minore fino al 10 che è il più maggiore
I: giusto, andiamo da numero minore al numero maggiore. Dall’1 andiamo verso il 10 non il contrario. Dal più piccolo andiamo al più grande.
MIRABEL: ma possiamo anche fare il contrario 10, 9 ,8 ,7, 6, 5, 4, 3, 2, 1
I: certo, se uno comincia a leggerlo dall’alto va dal minore al maggiore, invece, se comincia a leggere dal basso andrà dal…
MIRABEL: dal maggiore al minore
I: qualcos’altro? Finite le idee?
MIRABEL E ALTRI: si
I: Leonardo, cosa ci vuoi dire del tuo disegno? Che cosa avevi deciso di fare?
LEONARDO: ho deciso di fare quello
I: si, quale idea avevi quando l’hai disegnato?
LEONARDO: avevo l’idea di non fare i numeri ma solo scrivere. Dopo Berin mi ha detto che dovevo fare i numeri allora ho fatto i numeri
I: all’inizio lui aveva scritto solo le parole
BERIN: lui voleva copiarmi perché non sapeva cosa fare poi gli è venuto in mente di scrivere in lettere
I: quindi a te i numeri piacciono in lettere?
LEONARDO: in lettere oppure anche in numero
I: qualcuno ha delle domande per Leo?
MIRABEL: perché i numeri hanno le forme di qualcosa? Tipo il 3 è a forma di serpente
I: ok Mirabel sembra un serpente. Non penso che Leonardo abbia voluto fare un serpente altrimenti avrebbe fatto anche la lingua
BERIN: sarebbe un serpente a due teste
GIADA: il 9 può essere una balena
I: Mirabel, la tua è una bella idea! Eventualmente, più avanti, quando faremo un’altra creazione matematica, potrai scegliere di prendere i numeri e trasformarli in animali. È vero che qui puoi vedere degli animali o degli oggetti ma Leonardo non ha scelto di trasformare i numeri in animali o oggetti.
BERIN: non solo in animali perché pupi trasformare il 7 in una mazza da golf
I: sì, anche in oggetti abbiamo detto
