Sonia Sorgato, classi seconda e terza (stessa classe per 2 anni consecutivi), Milano
Pattern dei pinguini (classe seconda)
Videolezione del 7 maggio: gruppo Sara, Matteo, Ginevra, Sveva
Sonia: oggi faremo un lavoro insieme, vi farò vedere un’immagine, ne parleremo insieme e poi alla fine potremo anche disegnarla sul quaderno.

Ora possiamo iniziare: guardate bene come è fatta questa immagine e ditemi cosa ne pensate […]. Cominciamo a descriverla… chi vuole iniziare?
Sara: io vedo dei pinguini blu che prima ce ne sono 2, 4 poi e poi ne vedo 7.
Sonia: …e poi ce ne sono 7.
Sara: può essere che erano un gruppo, 2 pinguini se ne sono andati e il risultato può essere 7.
Sonia: quindi tu ti stai immaginando una storia, interessante…sentiamo Matteo.
Matteo: io come Sara prima vedo i pinguini prima 2, poi 4 e poi 7, 2+4 fa 6 e 6+7 fa 13, perché se faccio 7+7 fa 14 ma meno 1 che è il 6 fa 13 e già c’è l’operazione 2+4+7, oppure accorciata 6+7.
Sonia: quindi tu vedi dei gruppi di pinguini da sommare, da mettere insieme, ok sentiamo altre idee…
Ginevra: i pinguini sono blu…
Sonia: ok, questi pinguini hanno una disposizione particolare? Immaginate di disegnare questi pinguini come possiamo fare?
Sveva: nel primo gruppo ce ne sono 2, nel secondo 4 e nel terzo 7.
Sonia: avete osservato bene, avete detto che sono dei pinguini blu, avete detto che sono disposti in gruppi, Sara e Matteo hanno anche pensato a dei problemi che si possono immaginare… avete da aggiungere qualcosa?
Matteo: la prima non è messa in scala perché se mettevano il secondo pinguino sopra il primo veniva solo una riga in verticale, le altre sono messe in scala, nella seconda ce ne sono 3 sotto e 1 sopra, nell’ultima ce ne sono 4 poi 2 e in alto 1.
Sonia: siete d’accordo con Matteo?
Sveva: se togliamo l’ultimo gruppo troviamo l’inizio della tabellina del 2.
Sara: può essere anche che era un gruppo di pinguini che hanno fatto una piramide e poi 2 pinguini si sono stancati di fare una piramide e poi anche 4 si sono stancati e poi loro continuano a fare la piramide.
Sonia: se i pinguini dovessero continuare a fare le piramide come potrebbe essere la quarta piramide.
Sara: la piramide sarebbe senza pinguini perché se ne vanno i pinguini.
Sonia: ma se dovessimo disegnare una piramide che viene dopo la terza come potrebbe essere?
Sara: una piramide un po’ strana così (fa dei gesti per indicare delle linee).
Matteo: mi è venuta un’idea sentendo Sara: i pinguini si sono spostati per fare una piramide grande.
Sveva: a me la cosa che avevano detto Sara e Matteo è giusta, secondo me la piramide l’ultima piramide è più alta.
Sonia: in che modo potrebbe essere più alta? Come potremmo farla?
Ginevra: prima ci sono 7 pinguini.
Sonia: come potrebbe essere la quarta piramide. Abbiamo detto che potrebbe essere più alta rispetto alla terza.
Sveva: secondo me la quarta piramide non è come tutte le altre, sarebbe tutta intera. Sarà un triangolo. La terza non è un triangolo perché c’è l’ultimo pinguino dell’ultima riga che non è dentro il triangolo.
Matteo: mi sembra che ho scoperto qualcosa, mi sa: se la prima piramide aveva 2 pinguini, poi è avanzato di 2, la terza ha avuto 3 pinguini in più quindi secondo me la quarta ha 11 pinguini perché 7+4 fa 11.
Sonia: immaginate già come potrebbe essere fatta questa piramide?
Sara: la quarta potrebbe anche essere un quadrato.
Sonia: direi che possiamo provare a disegnare. Che titolo mettiamo?
Sara: la creazione dei pinguini!
I bambini disegnano i primi 3 gruppi, la discussione ricomincia per cercare un modo per disporre gli 11 pinguini.
Sonia: come possiamo fare per la quarta?
Sara: devo prendere un foglio e fartela, faccio dei cuoricini perché non so fare i pinguini.
Ginevra: possiamo farne 10.
Sara: Matteo ha detto che i pinguini della quarta piramide sono 11.
Ginevra: come fa a saperlo?
Sonia: è una bella domanda, dobbiamo chiederlo a Matteo.
Ginevra: ho capito: prima cosa facciamo 5 sotto, 3 sopra, poi 2, e poi 1!!!
Sonia: siete d’accordo?
Bambini: sì!!!
Sonia: e se dovessimo disegnare il quinto gruppo?
Ginevra: ma io non ci sto! 6 sotto, 4, 3, poi 2 e poi 1.
Sonia: quindi quanto sarebbe?
Ginevra: 16!
Sonia: Matteo tu avevi detto che dal primo al secondo se ne aggiungono 2…
Matteo: poi se ne aggiungono 3 per arrivare a 7.
Ginevra: poi 4 e poi 5.
Sara: vorrei proprio sapere chi ha fatto questa creazione matematica!
Videolezione dell’11 maggio: gruppo Sara, Matteo, Sveva
I bambini disegnano sul quaderno una tabella in grado di mettere in relazione il numero del gruppo con il numero dei pinguini presenti nel gruppo.
Maestra: quanti pinguini ci sono nel numero 4?
Matteo: se ricordo bene…
Sara: 11!
Matteo: nel numero 5 o 15 o 16.
Sara: aspetta (va a guardare sul quaderno) 12.
Matteo: no, è 16, mi sa.
Sveva: era 16.
Matteo: sì perché è lo stesso ragionamento dell’altra volta: nel primo gruppo se ne aggiungono 2, nel terzo se ne aggiungo 3 e fa 7, nel quarto se ne aggiungono 4 e 7+4 fa 11, nel quinto se ne aggiungono 5 e 11+5 fa 16.
Maestra: andiamo ora avanti un po’, io proverei però senza disegnare: proviamo a capire nel sesto gruppo quanti ce ne sono.
Matteo: io lo so, lo so, mi sembra 22.
| GRUPPO | NUMERO DI PINGUINI |
| 1 | 2 |
| 2 | 4 |
| 3 | 7 |
| 4 | 11 |
| 5 | 16 |
| 6 | |
| 7 | |
| 8 |
Sara: nella prima colonna stiamo facendo 1, 2, 3, 4, 5… nell’altra colonna 2, 4, 7, 11, 16… secondo me nel sesto gruppo di pinguini…
Sveva: io ci ho pensato, secondo me è 20.
Sara: anche per me è 20.
Maestra: come avete fatto a dire 20? Che ragionamento avete fatto?
Sveva: non può essere 14 e ho detto che era 20.
Maestra: ma perché proprio 20 e non 30, e non 50 o 21…?
Sveva: il 20 era il numero che veniva dopo. Prima c’era l’11, il 16 e poi ho pensato a 20.
Sara: ho pensato anch’io a 20 come la Sveva…
Maestra: sicuramente nel sesto gruppo i pinguini aumentano…
Sara: i pinguini aumentano, ho pensato come la Sveva, i pinguini aumentano…
Maestra: aumentano ma non tantissimo…
Matteo: secondo me è 22 perché al gruppo 4 c’erano 11 pinguini, poi sono aumentati di 5 con il gruppo 5 e siamo arrivati 16 e quindi ora faccio 16+6 che fa 22.
Maestra: cosa ne pensate Sara e Sveva? Voi avete pensato a 20.
Sara: puoi ripetere Matteo che non ho capito bene.
Matteo: secondo me è 22, spiego da capo: parto dal gruppo 4 dove c’erano 11 pinguini poi siamo aumentati di 5 come il gruppo che era di 5 e siamo arrivati a 16, e poi secondo me dobbiamo aumentare di 6 per il gruppo 6.
Sara: può essere come ha detto Matteo. La tua cosa è giusta può essere anche 22. Mi spieghi una cosa? Perché devi fare così? La prima parte l’ho capita, mi ripeti la seconda parte?
Matteo: noi siamo aumentati come nel gruppo che eravamo. Nel gruppo 4 siamo aumentati di 4 come il gruppo dove eravamo arrivati.
Sara: tu hai detto 22, secondo me è 20 secondo te è 22.
Matteo: sì.
Sara: non per criticare…
Matteo: ognuno dice la sua opinione, uno fa in un modo e uno in un altro.
Sara: se prima erano un gruppo poi se ne sono andati, può non essere 22.
Maestra: però Sara abbiamo detto che aumentano.
Sara: noi abbiamo detto 20, io e Sveva, tu Matteo pensi 22 perché così tanto Matteo?
Matteo: perché il numero non aumenta sempre uguale prima aumenta di 2 poi non aumenta ancora di 2 ma aumenta di 3 e diventa 7 perché secondo me era nel gruppo 3, poi dopo 7 sono aumentati di 4 e sono 11, poi 5 ed erano 16, poi 6 e diventano 22, perché secondo me aumentano sempre di 1 ma non nel senso che da 11 arrivano a 12 ma dal gruppo 1 al gruppo 2 aumentano di 2, poi di 3, poi di 4… secondo me.
Sara: Matteo intanto ti dico che hai fatto bene, hai ragionato bene però ora provo a ragionare come hai fatto tu Matteo, va bene? Hai ragionato benissimo, hai detto che è 22. Sono ancora un po’ in dubbio, quello di Matteo è giusto e il nostro sbagliato? Sono ancora in dubbio.
Maestra: Sveva tu cosa ne pensi?
Sveva: non sono tanto d’accordo.
Sara: mi sembra più giusto quello di Matteo ora.
Sveva: ora ci ho pensato meglio e forse è più giusto quello di Matteo.
Maestra: prova a dirmi come ha fatto: perché bisogna aggiungere 6 e non un altro numero?
Sara: secondo me è 22.
Maestra: come faccio a sapere che numero di pinguini ho nel gruppo che viene dopo?
Sara: aumentano sempre di più, prima 2, poi 3 e poi 4.
Maestra: per il settimo gruppo cosa mettiamo?
Sveva: devo fare 22 + 7 che fa…
Sara: fa 29.
Matteo: io voglio arrivare fino al 13.
Maestra: da 29 cosa faccio?
Sara: 29 + 8 che fa 37.
[…] si continua fino al tredicesimo gruppo.
Maestra: cosa faccio per sapere che numero di pinguini ho nel
centesimo gruppo? Cosa devo sapere? Facciamo finta di averli scritti ma non lo facciamo veramente. Cosa dovrò fare?
Sara: devo sommare dove c’è su al 99 nella seconda colonna +100 e poi metto il risultato e poi se vuoi andare avanti puoi andare avanti finché vuoi.
Maestra: quindi bisogna sommare il numero di pinguini del 99esimo con 100.
Sara: e poi vai avanti così.
Matteo: io sono arrivato a 131 di pinguini, poi se uno vuole può andare avanti.
Sara: anche gli altri gruppi faranno questo lavoro e poi viene uguale?
Maestra: i risultati sono uguali ma i ragionamenti diversi.
Il pattern dei caschi (classe terza)

Giorgio spiega come si trova il numero dei caschi alla posizione 1000 (filmato).
Dalla creazione di Malik al disegno di Solayman (classe terza)


Sonia: oggi lavoriamo sulla creazione di Malik e sul disegno di Solayman, il disegno di Sole mi ha fatto venire in mente questa sequenza di immagini.
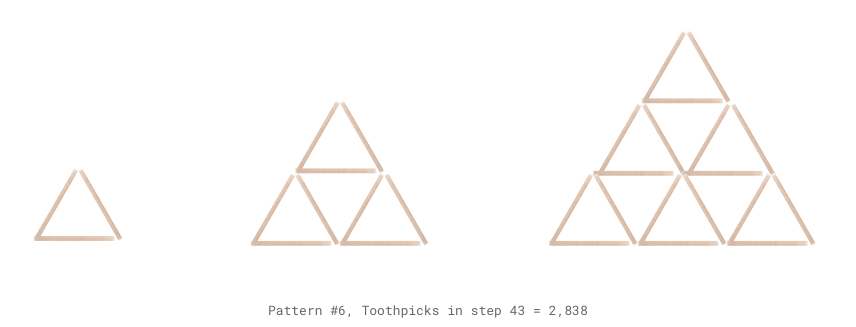
I bambini disegnano sul quaderno la sequenza delle prime tre immagini.
Antonio: a me è venuto in mente il lavoro dei caschi, mi sembra un po’ uguale.
Sonia: vediamo se funziona allo stesso modo, abbiamo scoperto il meccanismo dei caschi. Vi ricordate? Cominciamo a capire cosa possiamo fare per capire il meccanismo.
Matteo: io l’ho capito, finisco di disegnare e poi lo spiego.
Alessandro: mi sembra la tabellina del 4, ci sono 1 poi 4 bicchieri e poi 8, ci sono 8 triangoli, dopo quindi dobbiamo mettere 12 bicchieri.
Sonia: secondo Alessandro è la tabellina del 4, vediamo se tutti sono d’accordo su questa osservazione. Pensiamo anche alle domande che possiamo farci per capire il meccanismo,.
Alessandro: io mi sono fatto questa domanda: ho guardato il + come 3 +1=4 ovviamente si mette il x e non è possibile che siano più di 3.
Sonia: scusa giusto per capire se ho capito: se io passo dalla prima alla seconda cosa succede?
Ale: non devi fare con il +, per me è la tabellina del 4.
Sonia: gli altri bambini sono d’accordo che è la tabellina del 4?
Sara: Alessandra ha detto la tabellina del 4, io non ho capito che cosa c’è della tabellina perché io non la vedo la tabellina del 4.
Sonia: tu non sei d’accordo con Alessandro.
Sara: se mi fa capire meglio dov’è questa tabellina del 4.
Solayman: io l’ho capito dov’è la tabellina del 4.
Sonia: tu sei d’accordo con Alessandro, prova a spiegarci.
Solayman: solo nel secondo è la tabellina del 4.
Alessandro: se non hai capito questa è la mia descrizione: fai finta che la prima immagine non c’è e concentrati solo sulle altre due, nella seconda figura ci sono 4 triangoli, conta anche quello di traverso.
Sara: ma non è che devo contare anche quello all’ingiù
Alessandro:ma scusa è sempre un triangolo, se mi giro divento Giovanni?
Sara: ho capito ma se faccio una costruzione con i bicchieri quello non lo conti quando lo vedi nella realtà e quindi se tu fai una costruzione con due bottiglie un po’ staccate non è che guardare la parte libera e come se non lo dobbiamo contare, ti ricordi quando abbiamo disegnato la creazione di Malik, Sonia non riusciva a capire allora io li ho colorati.
Secondo me è la tabellina dell’1, del 3 e del 5, quella del 4 non ci sta perché non si devono contare quelli a testa in giù.
Alessandro: io però non avevo finito, per me ci sono 4 triangoli nella seconda figura, il triangolo cavolto è sempre un triangolo
Sara: sì ho capito però lì non dovrebbe esserci niente che abbiamo visto la foto.
Ale: posso dirti la mia opinione? Nella terza figura ce ne sono 8 quindi per me è la tabellina del 4.
Sara: ma scusa se tu conti anche quelli a testa in giù ce ne sono 9.
Matteo: 9 o 6.
Alessandro: ma Sonia allora come facciamo? 1, 4 e 9 ma nella tabellina del 4 non c’è il 9.
Giorgio: comunque andremo avanti all’infinito, perché i numeri sono infiniti, le tabelline il +, tutto quello che c’entra con i numeri è infinito.
Antonio: a me sembra che la tabellina del 4 è giusta, ma come aveva detto Giorgio sul lavoro dei caschi raddoppio e aggiungo 1. La tabellina del 4 è giusto quello che ha detto Ale ma nella terza figura raddoppio e aggiungo 1.
Matteo: volevo dire che nella prima c’è un triangolo in basso, nella seconda 2, nella terza 3.
Sara: tu hai detto che nella terza sono 4, tu sta contando solo insù.
Matteo: ma io sto parlando di quelli giù.
Sara: allora sì. Io sono d’accordo su quello che ha detto Matteo ma aggiungerei una cosa, è vero quello che ha detto Ale se giri una cosa la forma non cambia, ma se voi immaginate la creazione di Malik senza gli spazi, ci sono questi rettangoli è diversa da quella che ha fatto prima perché Malik aveva utilizzato gli spazi e qua non li dobbiamo proprio contare gli spazi perché se no prenderebbero le linee degli altri triangoli e poi secondo me non è giusto, è giusto come ha detto Ale, anche quello che ho detto io è giusto.
Sonia: allora mi sembra che ci siano due idee: la prima idea è quella di considerare solo i triangoli colorati come nel disegno di Sole.
Sara: è quello che volevo dire, è giusto come ha fatto Sole perché quella è la costruzione, si può decidere se il cielo sono quelli bianchi o quelli di azzurro. Secondo me quella di Ale è sbagliata.
Sonia: ma guarda non ci sono idee sbagliate…
Giorgio: lo sai che un’idea sbagliata può diventare l’idea più giusta di tutte? Per esempio io sbaglio su questo e poi quella domande ci serve e risolve tutto il problema, mi è successo un milione di volte.
Sonia: ci sono due modi di vedere questa creazione: il modo di Sole e Sara e il modo di Alessandro che ha considerato tutti i triangoli anche quelli capovolti. A questo punto dobbiamo decidere se lavorare su quello che hanno visto Sara e Matteo oppure sul modo che ha trovato Ale.
Ginevra: votiamo!
Il giorno dopo:
Sonia: ieri avevamo deciso di lavorare sulle sequenze con i colori. Cosa potremmo fare per capire il meccanismo della macchina di cui parlava Giorgio nel lavoro sui caschi. Davide e sra avevano fatto una cosa che aveva permesso a Giorgi di capire il meccanismo.
Sara: avevamo fatto la tabella!
Giorgio: io avevo capito che dovevo aggiunger e qualcos’altro.
Sara: noi avevamo fatto la tabella perché avevamo visto che con i pinguini ci era servita. Tu ci avevi dato la fotocopia dei caschi e ci è venuta in mente la tabella.
Sonia: poi ci era venuta in mente la macchina che fai entrare un numero.
Giorgio: quella macchina moltiplicava e poi aggiungeva 1, quindi 4+4 e poi + 1.
Sara: dobbiamo fare una tabella.
Sonia: dovete dirmi voi come farla perché io non ho le idee chiare, se per favore ci pensate voi.
Sara: possiamo fare una tabella come quella che abbiamo fatto con i caschi. Cambiamo la scritta e cambiamo i numeri.

Sonia: ora possiamo ragionare sulle colonne, per esempio dalla prima alla quarta…
Anto: si raddoppia…no aspetta, nella prima viene moltiplicato per 1, nella seconda per 2, nella terza per 3…
Matteo: è giusto, è strano, numero della figura e numero di tutti i triangoli…
Alessandro: è come una tabellina, sono delle tabelline.
Matteo: sì
Sara: sono d’accordo che sono delle tabelline, però è anche con il + perché dal quarto al quinto devo 1+4… aumenta di uno.
Matteo: si moltiplica per se stesso! Ho visto che i numeri vengono moltiplicati per se stessi: 1×1, 2×2, 3×3
Antonio: se tu fai una linea che porta dal 3 fino al 9 trovi il numero che porta alla quarta colonna
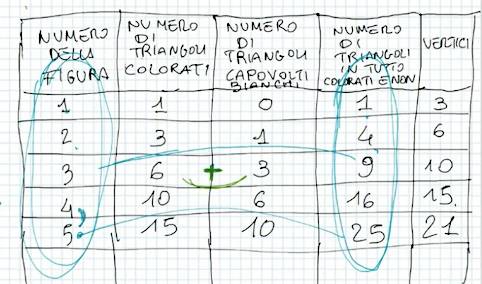
Antonio: sono i quadrati del numero.
