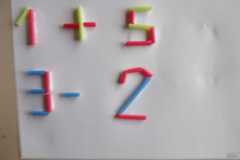Francesca Demartini, classe quinta, Pinerolo (TO)
2 marzo 2021
Discussione sulle creazioni
Abbiamo discusso in classe la creazione di Gabriel

Ins: guardiamo questa creazione. Questa è la creazione che ha fatto Gabriel la scorsa settimana. Guardatela con attenzione, prendetevi del tempo e poi provate a dire che cosa vedete di matematico in questa creazione alzando la mano.
Giacomo: secondo me di matematico nel lavoro di Gabriel c’è che le percentuali, come le ha scritte lui, sono matematiche. Perché 75% vuol dire ¾. è un po’ come dire ¾ e 25% è un po’ come dire ¼
Ins: siete tutti d’accordo con quello che dice Giacomo?
Giulia: si perché sono ….. si perché 75% vuol dire che ci sono ¾ di acqua?
Ins: secondo voi perché Giacomo dice proprio la frazione ¾?
Lulù: io non volevo dire proprio questo, secondo me lui ha scritto 75% perché i numeri sono un po’ ovunque, anche nell’acqua ci sono dei numeri.
Martino: io di matematico vedo anche il 75 e il 25, sono due numeri
Enea: io di matematico vedo anche il simbolo (si riferisce a %). Perché 75% quel simbolo vuol dire 75 parti di un intero.
Giulia: io non ho capito di quale intero?
Enea: è come se su 100 parti ne prendi solo 75. Quello è il 75%, invece per fare 25% vuol dire che hai 100 parti e ne prendi 25.
Martino: il mondo sembra uno zero
Giacomo: maestra io vorrei spiegare meglio il mio ragionamento. Allora praticamente 25 x 3 fa 75, perché 25-50-75, ecco perché ecco perché ho detto che 75% è ¾ perché 25 x 4 fa 100. Il mio è un po’ il ragionamento semplificato di quello di Enea possiamo dire.
Ins: ok grazie Giacomo, sei stato molto chiaro ad esporre il tuo ragionamento e il tuo punto di vista.
Giacomo: e poi volevo aggiungere che appunto 25% è come dire ¼
Giulia: si ora ho capito.
Ins: Giulia sei d’accordo con Giacomo? 25% vuol dire “di quattro parti ne prendo una”?
Giulia: si
Davide: si anche io sono d’accordo, 25% è ¼ perché se poi moltiplichiamo il 25 X 3 viene 75, quindi 75% è ¾. Perché è come dire che 25 parti su cento valgono ¼
Ins: quindi 25/100 è uguale a ¼ ?
Rebecca: si perché vogliono dire la stessa cosa, maestra ho capito sono frazioni equivalenti.
Ins: cosa vuol dire frazioni equivalenti?
Davide: sono frazioni che indicano la stessa quantità anche se sono scritti con numeri diversi. Ad esempio 25, 100, 1 ,4 sono numeri diversi ma possiamo dire che 25/100 è la stessa cosa di ¼
Enrico: quindi 75/100 equivale a ¾
Aurora: è come se prendessi 3 volte 25, su 100 parti.
Ins: ok, ora osservate i post-it che Gabriel ha usato nella sua creazione. Come vi sembrano?
Aurora: ci sono 10 post-it, però il 25 sembra che è tagliato. Il 25 sembra tagliato
Leon: ma guarda che ci sono 11 post-it non 10
Ins: Aurora dice che ci sono 10 post-it, Leon invece dice che ce ne sono 11. Secondo voi quanti post-it ha usato Gabriel?
Enea: a me danno l’idea che il 75% si riferisce all’acqua perché i post-it sono blu, invece il 25% si riferisce alla terra perché sono di colore verde
Alice: a me dà anche l’idea di un’operazione tipo 8 post-it azzurri più 3 che sono quelli verdi.
Giacomo; posso dire una cosa? Praticamente se contiamo bene… posso venire alla LIM? (…si avvicina alla Lim sulla quale era proiettata la creazione…) allora quindi contiamo bene i post-it blu non sono proprio 8 perché 8 vorrebbe dire 80% ma un pezzo è stato diviso a metà.
Ins: che cosa è stato diviso a metà? Tutta la quantità di port-it azzurri?
Giacomo: no solo un singolo post-it è stato diviso a metà.
Ins: quindi quanto vale un post-it?
Filippo: secondo me vale 1
Aurora: vale ½
Rebecca: ma no.., vale 10
Ins: 10 cosa?
Rebecca: vale 10%
Ins: allora perché ha messo mezzo post-it azzurro e non uno intero
Filippo: siccome i post-it azzurri sono 8, l’8° post-it è stato diviso a metà e rappresenta 5%. Perché se usava 8 post-it faceva 80%. Per fare 75% servono 7 post-it interi e un mezzo.
Alice M: perché un pezzettino vale 5% per questo ha usato solo mezzo post-it
Lulù: si perché se ogni post-it vale 10% la meta vale 5%, ha fatto così anche per la parte verde. Ha usato due post-it e mezzo, due che valgono 10 e uno da 5. Due interi fanno 20, più una metà fa 25.
Giacomo: io volevo dire che il 20% e quel 5 viene dalla divisione a metà di 1/8
Ins: prova a spiegarti meglio.
Davide: io non sono d’accordo, perché non ci sono solo 8 post-it così sarebbe 1/8 ma i post-it non sono 8, sono 10.
Leon: potrebbe essere 1/10
Ins: prova a spiegare meglio il tuo punto di vista?
Giacomo: allora se ci fossero 8 post-it azzurri ogni post-it sarebbe 1/8 quindi il post-it a metà è come se fosse metà di 1/8. Allora io prendo 8 post-it e i primi 7 li uso interi e l’ottavo lo divido a metà prendo ½ dell’ottavo post-it, ovvero ½ di un 1/8
Davide: a ok forse ho capito però secondo me è più corretto dire 7 post-it e mezzo perché così capisco bene che vuol dire 75%. Però un po’ ho capito anche quello di Giacomo
Rebecca: anche io come Davide
Ins: siete tutti d’accordo?
Leon: no, io dico che è più giusto dire metà di 1/10 perché in totale i post-it non sono né 7 né 8, ma sono 10 in totale. Quindi metà post-it è metà di 1/10
Giacomo: si ora ho capito, credo sia più giusto quello che dice Leon. Anche se pure il mio è giusto se guardo solo i post-it azzurri.
(anche tutti gli altri concordano con la conclusione di Leon)
Ins: Gabriel parlaci un po’ della tua creazione? I tuoi compagni sono riusciti a dire tutto quello che volevi rappresentare?
Gabriel: i miei compagni hanno già detto tutto. Io volevo divider la terra tra terra e acqua. Quindi 75% ¾ di acqua e 25% ¼ e poi ho usato i post-it per fare le quantità.
Edoardo: be si però potevi anche usare il grafico a torta. Io le percentuali le ho viste sul libro di geografia e c’è sempre il grafico a torta.
Ins: com’è fatto?
Edoardo: è un cerchio colorato con colori diversi, poi ci sono dei numeri con il simbolo % la parte colorata indica la percentuale di qualcosa
Davide: oppure puoi fare in un altro modo, fai una striscia di 100 quadretti e poi ne colori 75.
Leo I: anche secondo me come Davide.
Edoardo: maestra io vorrei provare alla lavagna a disegnare il grafico a torta (…va alla lavagna… disegna un cerchio con un cordino…) poi divido il cerchio in 2 parti una parte vale 75% e poi l’altra vale 25%
Davide: ma no che dici… devi dividere in 4 parti, poi ne colori una di verde che sono 25% e le altre 3 di azzurro che sono 75%
Edo: io invece volevo fare direttamente 75% a occhio
(mi sono dimenticata di fare le foto alla lavagna, Edoardo voleva procedere tracciando le fette del grafico a occhio, Davide invece propone di dividere il cerchio in 4 parti uguali)
Ins: ma così il 75% è preciso?
Garbriel: no, per niente.
Davide: maestra vengo io alla lavagna e ti faccio vedere cosa farei io (si aiuta con i quadretti della lavagna per dividere in 4 parti uguali)
Lulù: si secondo me è più corretto quello di Davide, su 4 parti ne ha colorata una che è la terra, invece di acqua ha colorato 3 parti su 4. Quindi proprio ¾. Anche se le 4 parti non mi sembrano proprio tutte uguali tra loro come l’ha disegnato lui.
Giacomo: io avrei un altro metodo (…va alla lavagna… fa un cerchio con la cordicella…divide l’intero in 10 parti che però non sono uguali tra loro) Allora il mio adesso non è preciso perché sulla lavagna non riesco a farlo preciso però posso spiegare il mio ragionamento. Allora divido in 10 parti uguali l’intero, qui non sono uguali però pensiamo che siano uguali, ogni fetta rappresenta 10%, per fare il 5% devo dividere a metà una fetta di torta, una fetta vale 10, meta fetta vale 5.
Ins: come vi sembra il ragionamento di Giacomo?
Rebecca: secondo me il ragionamento è giusto ma il disegno alla lavagna è stagliato perché le 10 fette non sono grandi uguali.
Ins: bene la prossima volta cercheremo di capire come rappresentare con maggiore precisione il grafico a torta usando il metodo si Edoardo, Giacomo e Davide e cercheremo di capire per ciascun metodo se può funzionare oppure no.
15 e 17 marzo 2020
Il problema del grafico a torta
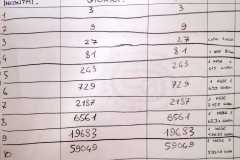
COME REALIZZARE UN GRAFICO A TORTA PER RAPPRESENTARE GRAFICAMENTE LE PERCENTUALI DELLA CREAZIONE DI GABRIEL: 75%, 25%

Fig 1. Creazione di Gabriel
OPZIONE 1 (proposta da Edoardo): fare un cerchio e poi fare due fette. La fetta piccola rappresenta il 25% la fetta grande rappresenta il 75%
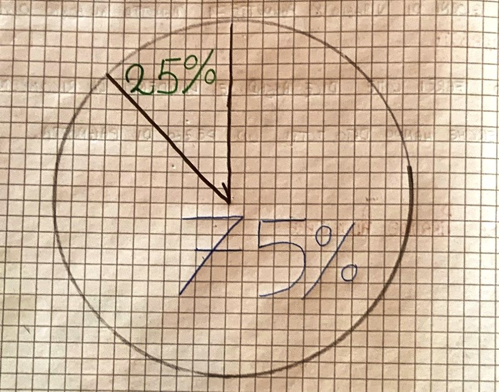
Grafico di Filippo
Ins: Come hai costruito il grafico?Filippo: ho fatto il cerchio con il compasso, poi ho diviso una piccola parte che rappresenta il 25% e la fetta grande vale 75%. 25% è poco quindi ho fatto una fetta piccola
Ins: Perché secondo te è giusto?
Filippo: io ho scelto questa perché sono riuscito a farlo e mi sembrava facile e anche perché le altre non le ho capite molto.
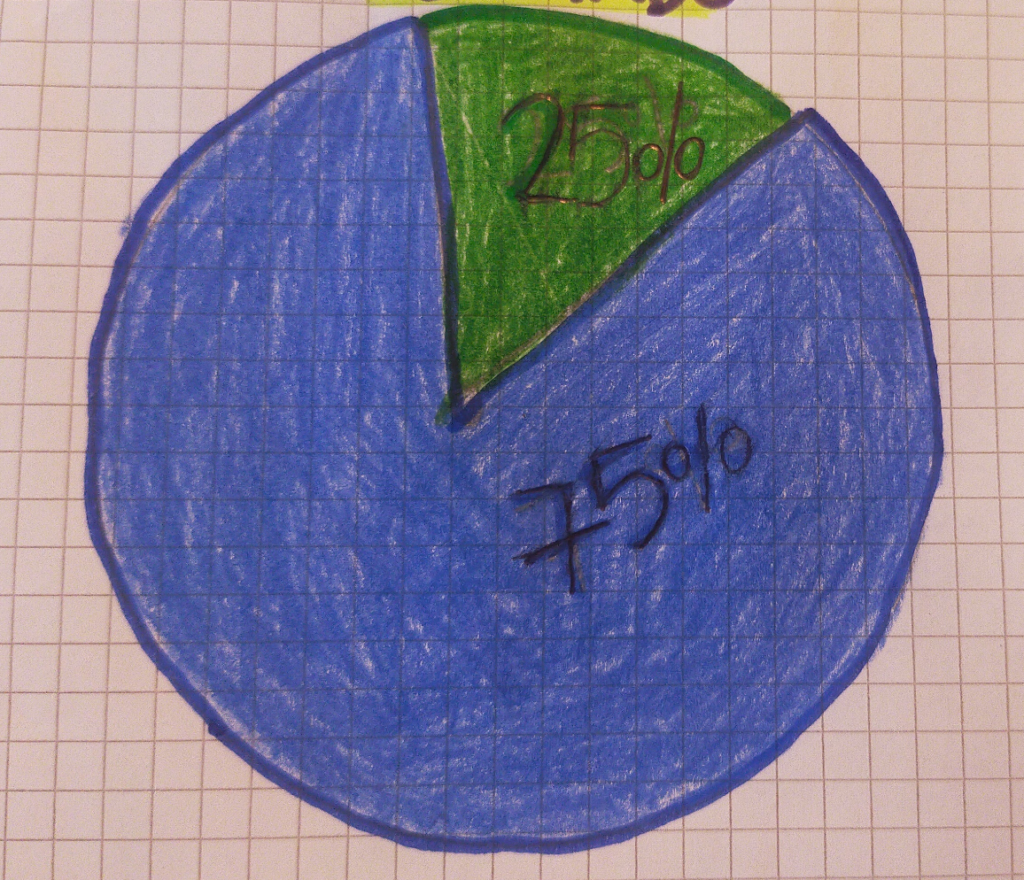
Grafico di Aurora
Ins: Come hai costruito il grafico?
Aurora: Ho usato il compasso per fare il cerchio, poi ho fatto un piccolo pezzo che rappresenta il 25% e tutto il resto il 75%
Ins: Perché secondo te è giusto?
Aurora: non so come dire, mi sembrava giusto. Nel senso… lo capivo di più

Grafico di Vincenzo: io ho usato la soluzione di Edoardo
Ins: Come hai costruito il grafico?
Vincy: ho usato il compasso per fare il cerchio e il righello per dividere le parti
Ins: Perché secondo te è giusto?
Vincy: mi sembra giusto perché secondo me, rappresenta bene quello che ha fatto Gabriel
Ins: Guarda il tuo grafico e poi quello dei tuoi compagni che hanno scelto lo stesso metodo. Il tuo spicchio che vale 25% è uguale allo spicchio di valore 25% di Aurora e Filippo?
Vincy: non sono uguali, il mio spicchio di 25% è troppo grande, ho sbagliato a farlo troppo grande, dovevo farlo più piccolo.
Ins: perché hai pensato di fare lo spicchio da 25% proprio così?
Vincy: la mia idea iniziale era di contare 25 quadretti per fare il 25% ma poi veniva troppo grande e allora non l’ho fatto così. Poi ho scelto di farlo così.
Ins: quindi ci hai ragionato per fare il 25% in questo modo o hai scelto a caso?
Vincy: ho scelto a caso e mi è venuto così
Davide: a me sembra quasi che Vincenzo abbia usato il mio metodo, però farse gli è venuto così a caso. Lui non ci ha pensato
Ins: Il metodo di Edo funziona? Si? No? Perché?
Filippo: non abbiamo usato le stesse misure per fare il 25% e il 75%, qualcuno ha fatto il 25% più grande come Vincenzo, io invece ho fatto il 25% più piccolo. Io vedo che in tutti e 3 lo spicchio del 25% è il più piccolo ma non sono piccoli uguali.
Aurora: secondo me funziona questo metodo
Filippo: secondo me no, perché tutti abbiamo usato dimensioni diverse per fare gli spicchi e non va bene.
Davide: infatti, qui il 25% non è ¼ dell’intero, quindi non va bene. L’hanno fatto a caso
OPZIONE 2 (proposta da Davide): fare un cerchio, dividerlo in 4 parti uguali. Colorare 3 parti azzurre per fare il 75% e una verde per fare il 25%
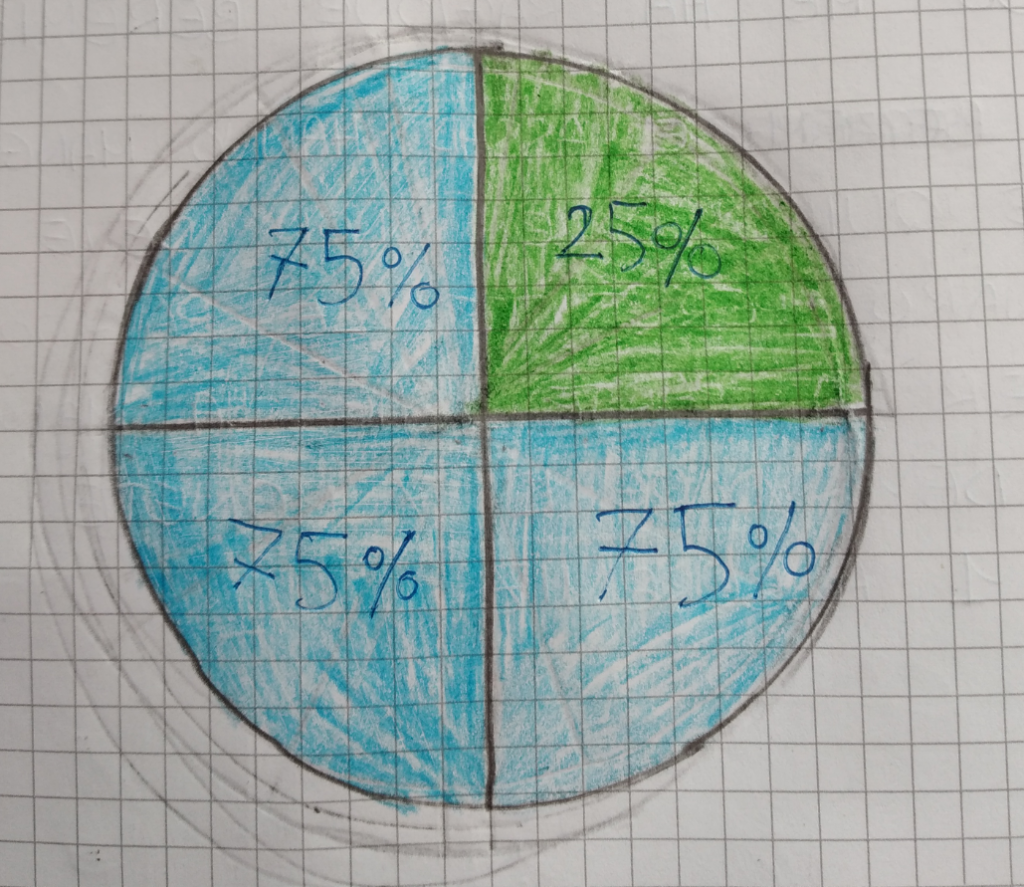
Grafico di Alice
Alice M. aveva problemi all’audio e non è riuscita a darci la sua spiegazione
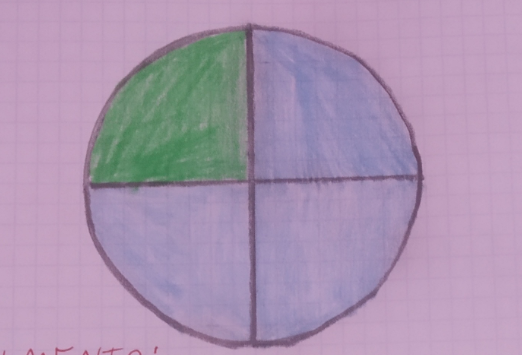
Grafico di Davide
Per realizzare il grafico a torta per prima cosa ho scelto il mio metodo. Poi ho tracciato un cerchio con il compasso e dal centro ho tracciato due linee (una verticale e una orizzontale). Quindi l’ho divisa in 4 parti (vuole assicurarsi che le 4 parti siano grandi uguali). Infine ho colorato ¾ di blu (quindi il 75%) e ¼ di verde (quindi il 25%). Secondo me questo metodo è esatto perché ¾ equivale a 75% quindi bisogna colorare 3 “spicchi” blu, è come colorare ¾ o 75% di un intero, la stessa cosa per lo spicchio verde (l’intero è stato diviso in 4 parti e ne prendo 1 pezzo, ovvero ¼, cioè 25%)
Davide: volevo aggiungere che io ho fatto partire le righe dal centro per assicurarmi di fare 4 fette uguali, perché se non fossero state uguali sarebbe stato impreciso, come quello di Edo
Ins: cosa c’è di uguale o cosa c’è di diverso tra il grafico di Davide e quello di Alice M.
Leo I: Sembra che 2 spicchi siano più grandi degli altri 2. Quelli in basso sono più grandi degli altri 2. Secondo me è sbagliato perché le 4 parti non sono grandi uguali.
Alice D: Secondo me Ali non avrebbe dovuto scrivere 75% in tutte e 3 le fette, ma solo alla fine. Perché così sembra che ogni fetta azzurra vale 75% ma non è così. Avrebbe dovuto fare la legenda a scrivere verde 25% e azzurro 75%
Giulia: io la penso come Leo, le 2 fette in basso sono più grandi delle altre 2. Poi ha sbagliato perché ogni spicchio non vale 75%
Alice D: no ogni spicchio vale 25%
Leo I: si perché 3 spicchi da 25 fanno 75%
Davide: io volevo dire che la somma totale degli spicchi deve fare 100, come l’ha fatto Alice M. la somma totale è 250 (75+75+75+25), invece il totale è 100% non 250%. Però il cerchio e gli spicchi sono abbastanza corretti, ha sbagliato solo a scrivere 75% 3 volte.
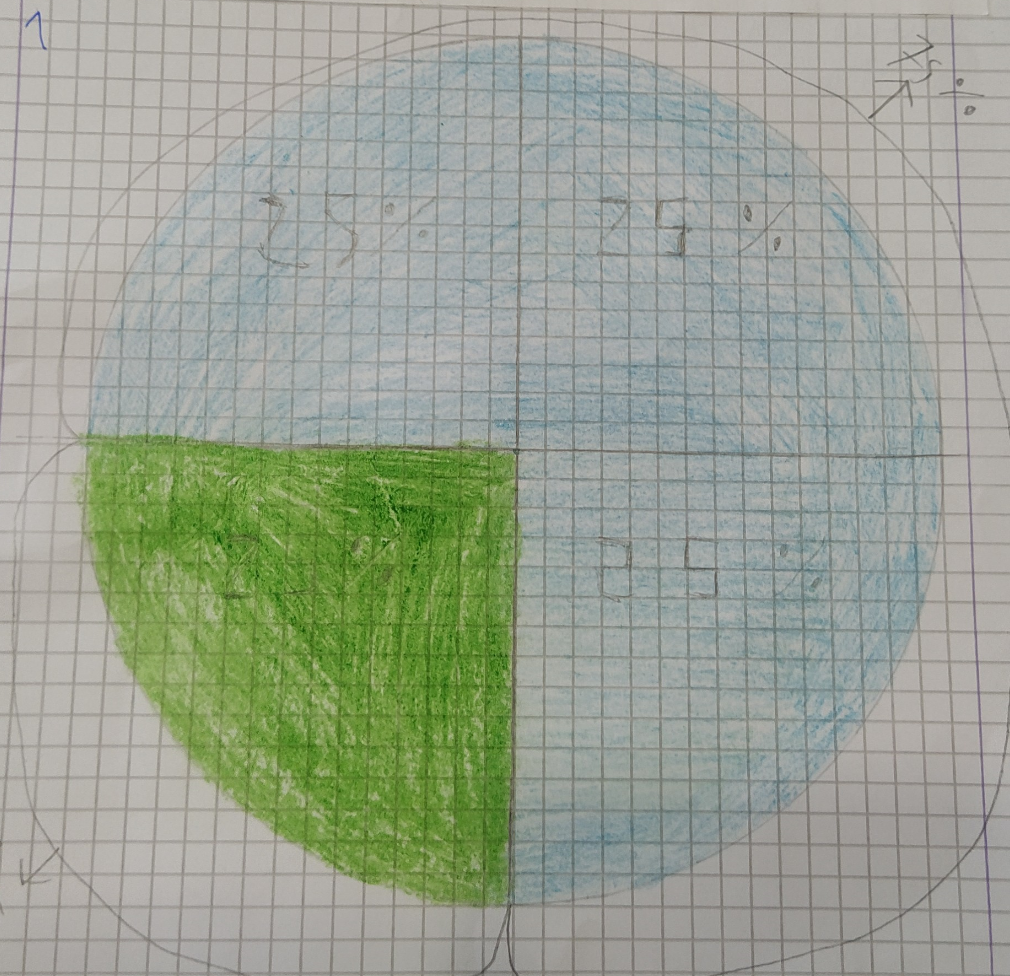
Grafico di Enrico
Con il compasso ho fatto il cerchio. Poi l’ho diviso in 4 parti. Poi ho colorato ¼ verde e i restanti ¾ azzurri. Io ho scelto il metodo di Davide perché era il più semplice e anche il più funzionale, perché ogni quarto era 25%. 25 x 4 = 100. Quello di Edo mi sembrava un po’ difficile perché non avevi righe, quello di Giacomo aveva troppi spicchi da fare e sono difficili.
Ins: in che senso nel metodo di Edo non avevi le righe? A quali righe ti riferisci?
Enry: volevo dire che con quello di Edo non lo facevi preciso ma l’angolo degli spicchi dovevi farlo a caso.
Ins: Prova a spiegare un po’ meglio perché secondo te il metodo di Giacomo è più difficile?
Enry: io non sono bravo a usare il righello e secondo me era giusto ma per me era troppo difficile e io ho fatto quello di Davide perché per me era più semplice
Ins: reputi giusti tutti e 3 i metodi?
Enry: quello di Edo non è giusto perché è impreciso, gli altri sono giusti perché sono precisi
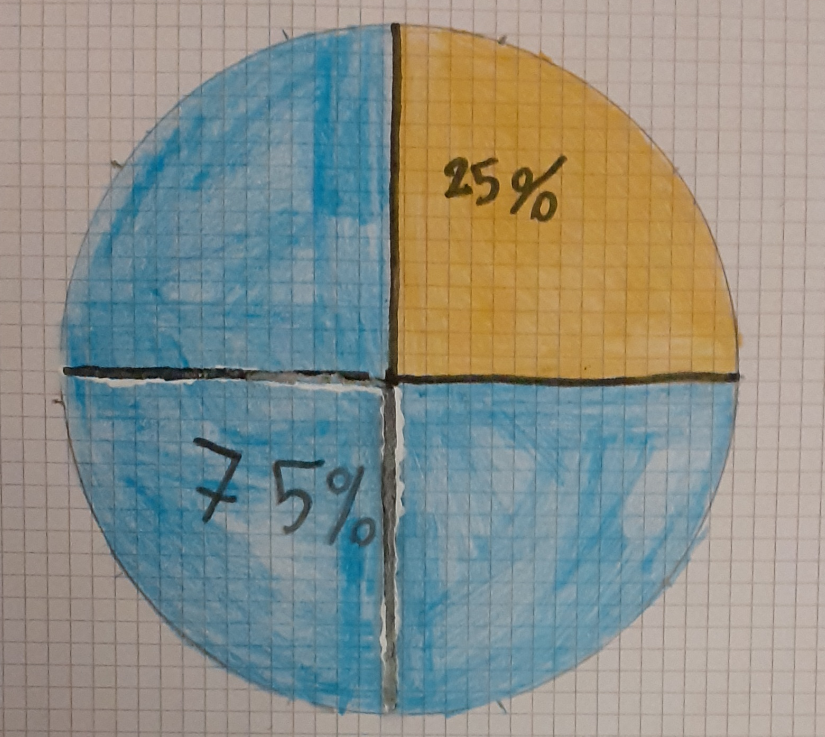
Grafico di Alice D.
Io ho fatto un cerchio e poi l’ho diviso in 4 parti uguali. Tre parti azzurre rappresentano il 75% e la fetta gialla, invece, il 25%. Secondo me è la scelta giusta perché 75 è il triplo di 25, quindi la parte del 75% è 3 volte più grande di quella gialla.
Alice D: Io ho scelto quella di Davide perché era la più facile da rappresentare ed era anche molto chiara. Io ero indecisa tra questa e quella di Giacomo, perché per me sono giuste entrambe. Però poi ho scelto quella di Davide perché era più facile. Quella di Edo, invece è sbagliata perché fai le fette a caso, non sei certo di fare davvero 25%.
Ins: ok ho capito. Come hai fatto a fare 4 spicchi uguali?
Alice D: allora ho fatto una riga in mezzo, cioè dove c’era il centro e ho usato il goniometro. E guardavo dove c’era 90°
Ins: perché 90° ?
Alice D: perché così formavo un angolo retto, perché tutti e 4 le fette sono di 90° , così arrivo a 360° e io so che 90° è ¼ di 360° così ero certa di fare bene.
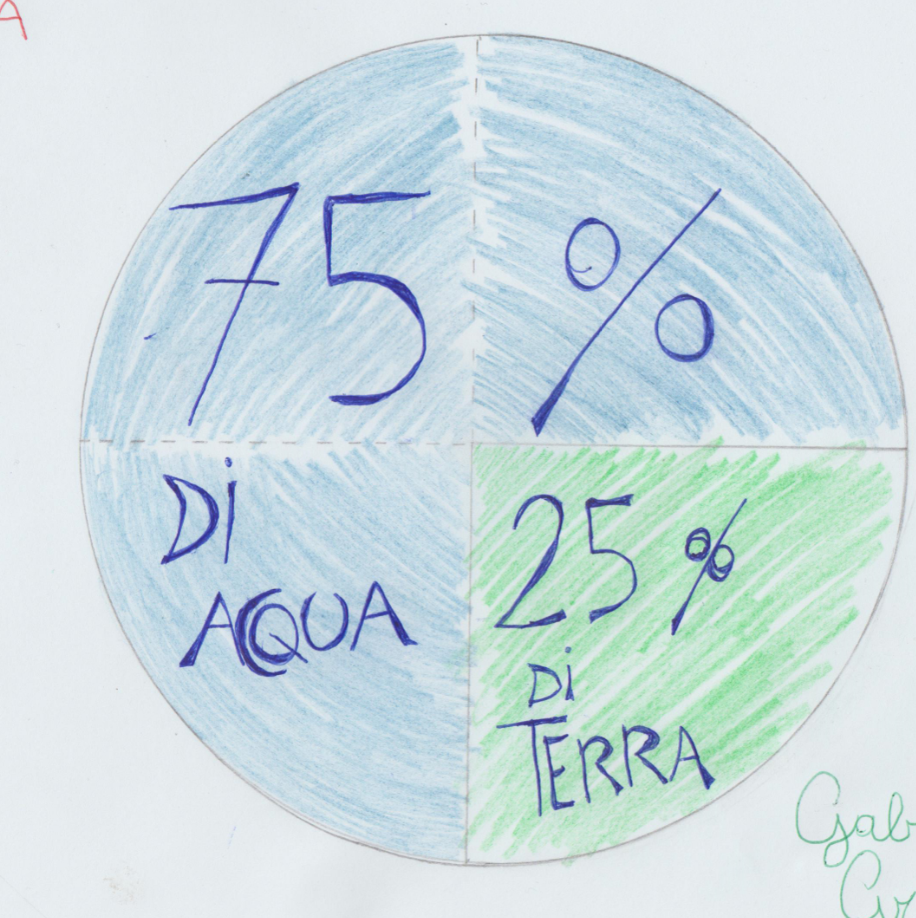
Grafico di Gabriel
Ins: Come hai costruito il grafico?
Gabriel: ho usato il compasso per fare il cerchio e poi ho usato la squadretta per fare le righe.
Ins: dato che tu hai fatto il grafico sul foglio bianco, come hai fatto a fare 4 fette della stessa dimensione?
Gabriel: in realtà ho fatto un po’ a caso e mi è venuto bene
Ins: ok dato che non sei sicuro che i 4 spicchi sono grandi uguali, cosa puoi fare per verificarlo?
Lulù: potrebbe provare a misurare l’ampiezza degli angoli degli spicchi, se vengono diversi allora sa che non sono uguali e non vanno bene
Gabriel: lo stavo dicendo io, devo misurare gli angoli, se sono tutti uguali, cioè di 90° allora il mio grafico è corretto

Grafico di Leonardo C.
Ins: Come hai costruito il grafico?
Leo C: io ho fatto il grafico con il compasso e poi ho fatto delle righe con il righello. Ho contato che la linea verticale, che passa per il centro era di 12 quadretti, quindi ho trovato la metà che è 6 e ho fatto un punto e poi ho fatto la seconda riga orizzontale perpendicolare all’altra.
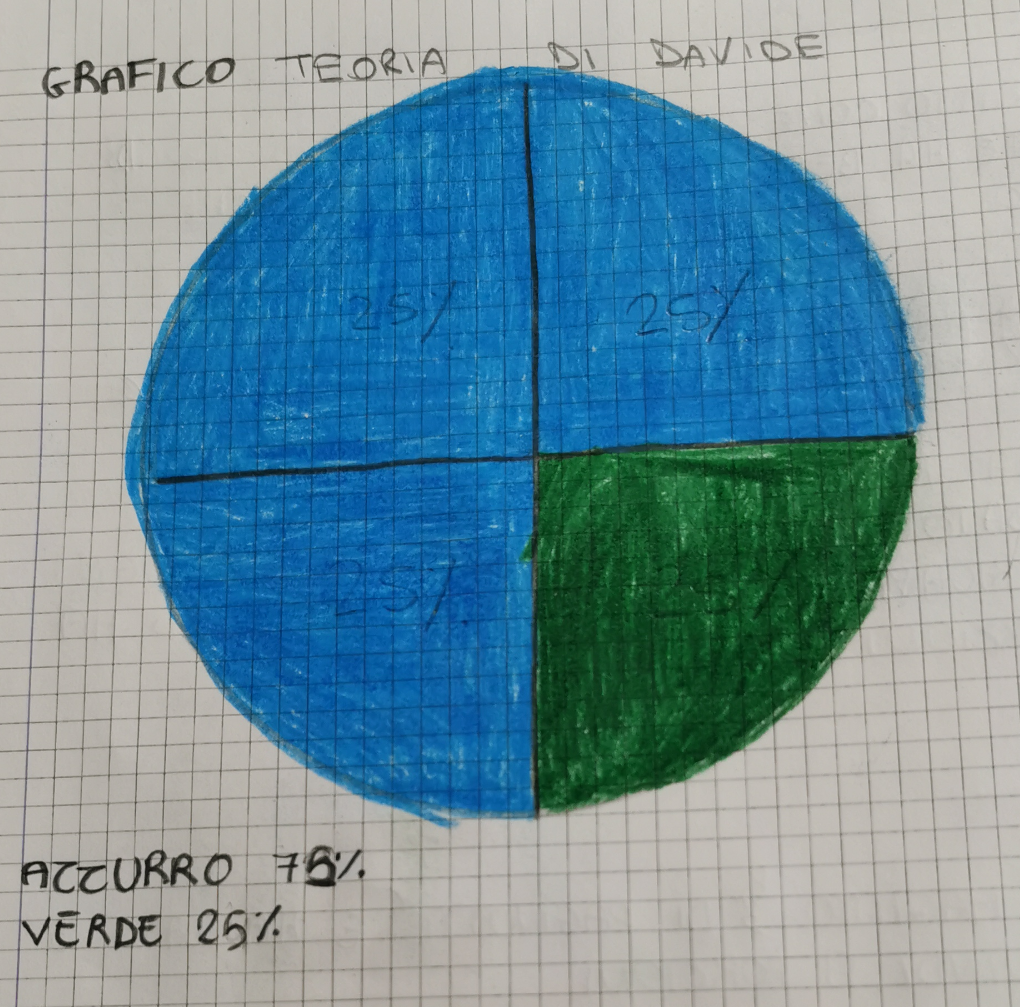
Grafico di Giulia
Ins: come fai ad essere sicura che i 4 spicchi siano della stessa dimensione?
Giulia: io ho sbagliato le 4 parti non sono uguali, sono tutte diverse.
Ins: cosa puoi fare per aggiustare il tuo grafico
Giulia: posso misurare l’ampiezza degli spicchi con il goniometro
Alice D: si ma prima devi trovare il giusto centro del cerchio, è quello dove metti la punta del compasso quando fai il cerchio.
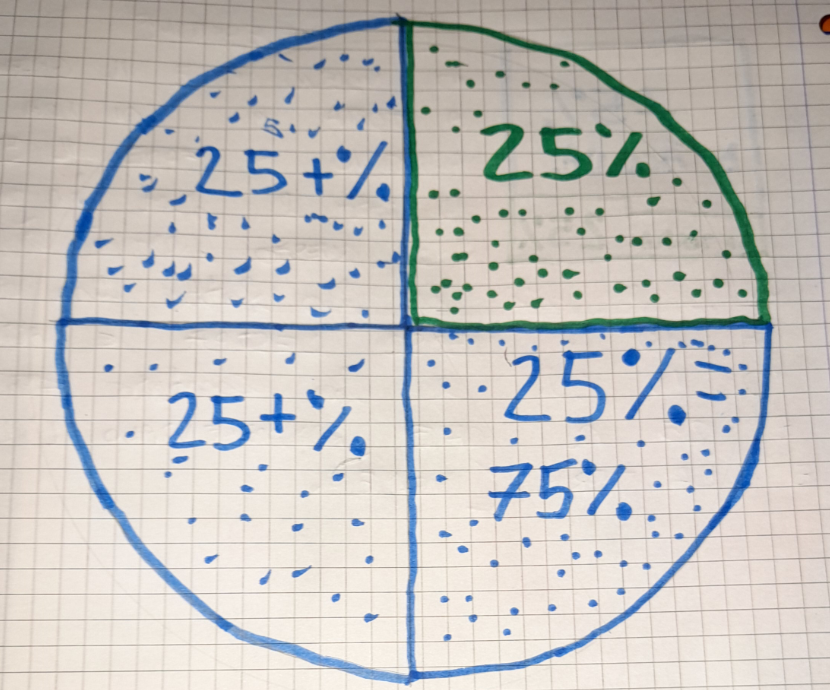
Grafico di Leonardo I.
Io ho scelto di usare questo metodo perché mi sembra il più giusto. Io ho rappresentato un cerchio che ho fatto con il compasso e ho capito che una parte delle 4 vale 25%
Ins: come hai fatto a capire che una parte vale 25%?
Leo: le 4 parti, allora ogni parte vale 25%, perché ogni quarto vale 25%
Poi per fare le quattro parti uguali mi sono aiutato con il punto del compasso, lì dove c’era il punto nel centro ho poi fatto le due righe
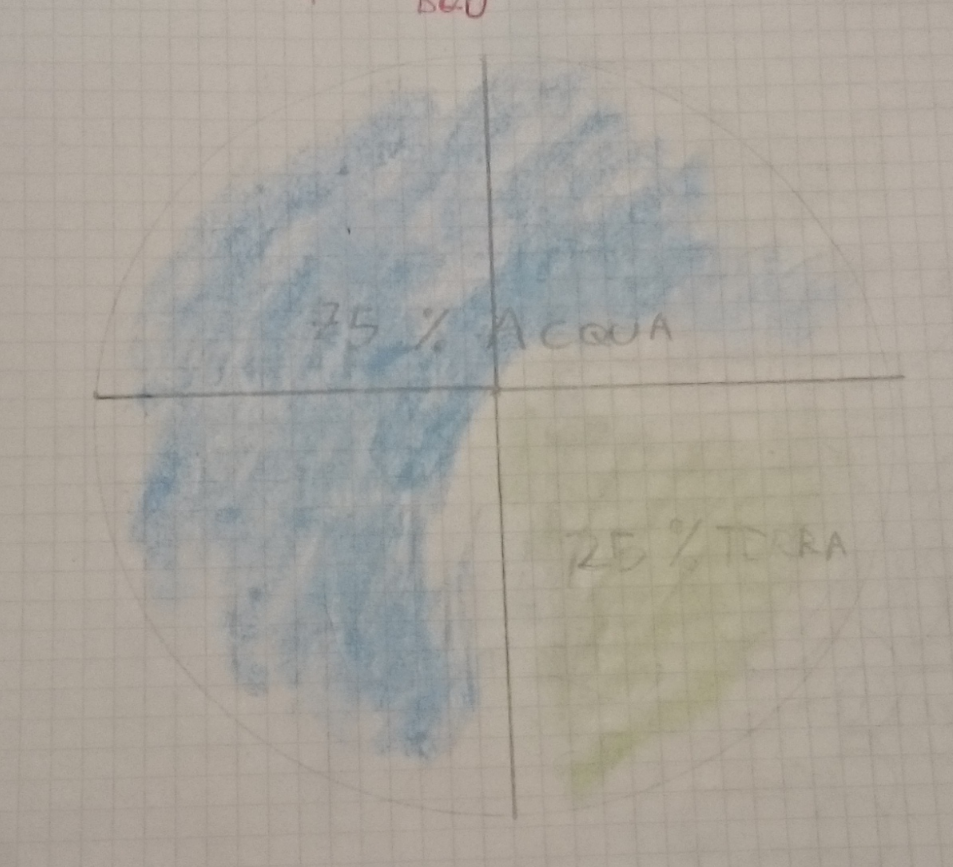
Grafico di Leon
Ho iniziato con il metodo di Edo ma alla fine mi sono trovato su quello di Davide, alla fine funziona perché sono riuscito a farlo. Ho fatto un cerchio poi ho colorato ¼ verde 25% e ¾ blu 75%
Ins: prova a spiegare un po’ meglio. In che senso sei partito dal metodo di Edo e poi ti sei trovato su quello di Davide?
Leon: allora io ho iniziato come Vincenzo facendo uno spicchio ma poi ho capito, al contrario di Vincenzo, che sarebbe stato più giusto usare il metodo di Davide. Perché con quello di Edo non ti diceva molto. Invece quello di Davide ti faceva proprio capire che ¼ è 25%


Grafico di Rebecca
Ho scelto il metodo di Davide. Per realizzarlo ho fatto un cerchio poi l’ho diviso in quattro parti uguali e ho colorato di verde ¼ che è il 25% e di blu i ¾ che sono il 75%. Infatti se fai 100 : 4 il risultato è 25 e se fai 25 x 3 fa 75
Ins: come hai fatto a fare 4 fette uguali?
Reby: ho contato i quadretti dentro gli spicchi
Ins: come hai fatto con i quadretti che non erano interi
Reby: ho contato a metà
Ins: però in alcuni casi c’era un pezzettino piccolissimo di quadretto, come l’hai contato?
Reby: era un po’ difficile, forse non è preciso. Forse era meglio usare il metodo di Alice D. perché è più preciso del mio
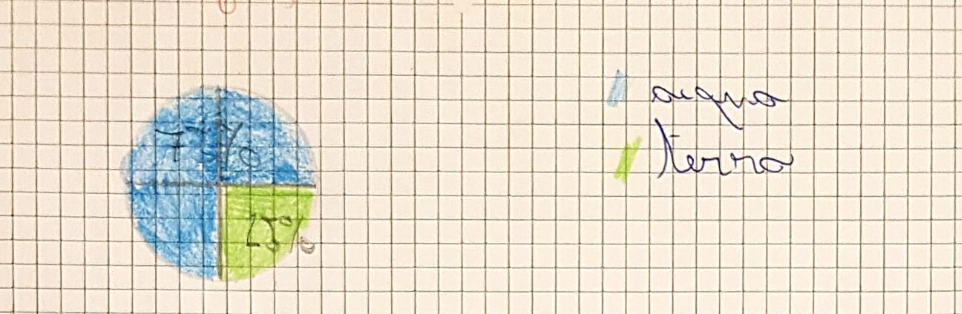
Grafico di Edoardo
Ciao Francesca, ti volevo dire che il metodo che avevo proposto io è impreciso e che quindi ho utilizzato quello di Davide, l’ho scelto anche perché quando l’ho proposto durante la lezione mi sono subito accorto non era preciso. Io ho fatto un cerchio con il compasso, poi ho diviso il cerchio in 4 parti uguali (ossia tracciando all’interno 2 rette perpendicolari). Successivamente ho colorato 3 parti blu che indicano il 75% di acqua e una verde che indica il 25% di terra. Questo procedimento per costruire il grafico funziona perché ti fa notare in un modo veloce e preciso le diverse percentuali.
Edo: maestra mi hai colto alla sprovvista mettendo la mia, come ipotesi. Io so che non è giusta quindi non l’ho usata perché non va bene. Io me ne sono accorto subito.
Ins: non ti preoccupare Edo, bravo per essertene accorto e soprattutto grazie per aver tirato fuori questa opzione perché ci sta aiutando nella nostra riflessione. Anche le cose sbagliate ci possono aiutare a capire di più e meglio.
Ins: Il metodo di Davide funziona? Si? No? Perché?
Martino: secondo me è giusto ma non mette tanti dettagli tipo.
Ins: una cosa per essere giusta dev’essere ricca di dettagli?
Martino: No
Ins: Guarda lo spicchio verde del grafico fatto da Davide, rappresenta il 25%?
Martino: si
Ins: e i 3 spicchi azzurri insieme, che percentuale rappresentano?
Martino: 75%
Ins: quindi il grafico proposto da Davide è giusto o no?
Martino: per me no… poi…
Filippo: maestra voglio parlare io, secondo me è giusto perché lo spicchio verde rappresenta il 25% di terra cioè ¼ e lo vedi bene perché è solo 1 spicchio e poi i 3 spicchi blu, insieme rappresentano il 75% e messi insieme viene 100%. Quindi è corretto come metodo. Lo ha scritto anche Rebecca nel suo ragionamento.
Martino: ho capito, però per me è più giusto quello di Giacomo perché c’erano più dettagli
OPZIONE 3 (proposta da Giacomo): fare un cerchio, dividere il cerchio in 10 parti uguali, poi una delle 10 fette dividerla a metà. Colorare 7 pezzi e mezzo per fare il 75% e 2 pezzi e mezzo per fare il 25%
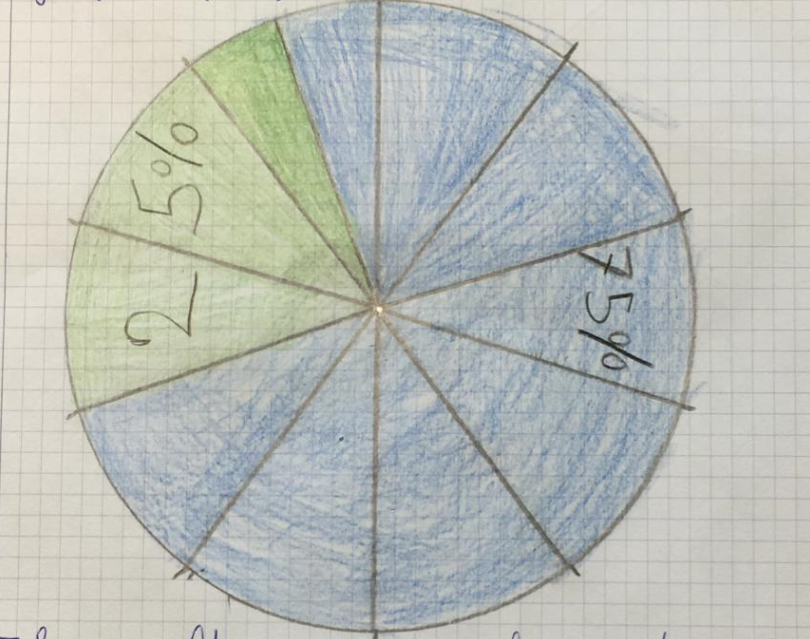
Grafico di Enea
Io ho scelto il metodo di Giacomo, i post-it della creazione di Gabriel erano 10 e gli spicchi sono 10. Per fare gli spicchi uguali ho usato il goniometro e ho fatto ogni spicchio di ampiezza 36°.
Enea: un angolo giro è di 360°, se devo fare 10 spicchi faccio 360°:10 e capisco quanti gradi è ampio ogni spicchio
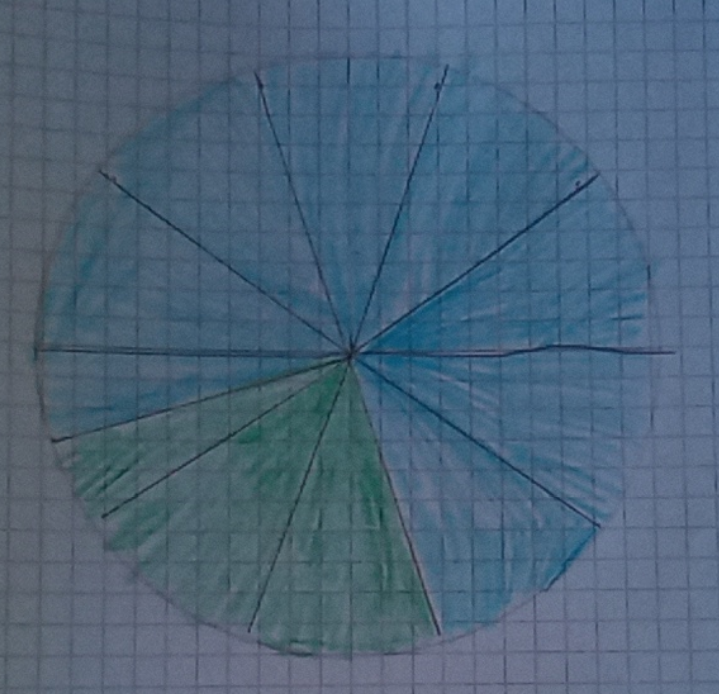
Grafico di Giacomo
Allora bisogna pensare che un angolo giro è di 360°. Visto che le fette che vogliamo ottenere sono 10, bisogna dividere per 10. Ottenuto il risultato ci si può aiutare con il goniometro, creando degli spicchi con ampiezza uguale al numero uscito dalla divisione. L’opzione proposta da me funziona perché il risultato che esce dalla divisione è facile da posizionare sul grafico grazie al goniometro. E vi assicuro che è impossibile sbagliarsi
Ins: qual è l’ampiezza di ciascuno dei 10 spicchi?
Giacomo: l’ampiezza di ogni spicchio è 36° come diceva Enea
Ins: qual è l’ampiezza dello spicchio diviso a metà?
Giacomo: l’ampiezza di metà spicchio è 18°, ho fatto 36°: 2. Devo ammettere che il mio metodo era un po’ difficile ma molto preciso se fatto bene. Perché rappresenta tutte e 10 le fette. Le fette si vedono con chiarezza e capisci con precisione quanto hai preso. Quello di Davide devo ammettere che l’hanno scelto in tanti e devo ammettere che era corretto ma io ho fatto un lavoro di precisione

Grafico di Lulù
Io ho fatto un cerchio con il compasso e ho diviso la torta in 10 parti uguali, di cui una delle 10 parti è stata divisa a metà. Perché ogni parte vale 10%, quindi se dividi una parte a metà ottieni 5%. Ho ottenuto il 75% prendendo 7 parti da 10 e una parte da 5. (7 x 10) + (0,5 x 10) = 70 + 5 = 75, ho fatto lo stesso per il 25%: ho preso 2 parti da 10 e una parte da 5 e ho ottenuto 25 (2 x 10) + (0,5 x 10) = 20 + 5 = 25
Ins: come fai ad essere certa che i 10 spicchi sono grandi uguali?
Lulù: gli spicchi li ho fatti ad occhio, solo per avere un’immagine nella mia testa. Ho diviso prima il cerchio in due parti uguali e poi ognuna delle due parti ad occhio in altre 5 parti, ho cercato di farle più o meno tutte uguali. Avrei potuto il metodo di Giacomo ed Enea per farlo più corretto
Ins: spiega un po’ meglio questa operazione che hai scritto (7 x 10) + (0,5 x 10) = 75%? Perché hai messo le parentesi. A cosa servono?
Lulù: perché ho preso 7 volte lo spicchio che vale 10% quindi 7 x 10 e poi 0,5 perché ho preso metà di uno spicchio e poi ho fatto per 10 perché metà spicchio era 5%
Davide: secondo me sarebbe stato più giusto scrivere 5 e non 0,5. Però forse ha ragione anche Lulù perché poi ha fatto 0,5 x 10 che fa proprio 5%
Ins: Lulù perché hai usato le parentesi?
Lulù: come a dire il calcolo è un po’ il ragionamento che ho fatto io. Quindi per far capire che qui c’è un calcolo e li finisce.
Ins: le hai usate per dividere i calcoli? qual è l’ordine?
Lulù: si, prima fai il calcolo che inizia con la prima parentesi e finisce alla seconda parentesi. Prima fai i calcoli nella parentesi e poi il resto.
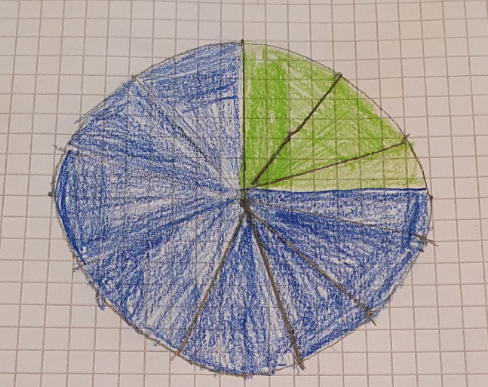
Grafico di Martino
Ho scelto l’opzione di Giacomo. Ho diviso il cerchio in 10 spicchi, come aveva detto Giacomo, e ho colorato gli spicchi secondo la creazione matematica di Gabriel. Il grafico a torta è come una torta che si deve dividere in fante fette uguali e si prendono quelle che interessano
Ins: come hai fatto a fare 10 spicchi uguali?
Martino: io ho fatto a occhio come Lulù ma ora mi sono accorto che era meglio fare come Giacomo ed Enea
Ins: Il metodo di Giacomo funziona? Si? No? Perché?
Enea: il metodo è giusto perché è preciso, se usi il goniometro non puoi sbagliare
Alice D: Si, secondo me è giusto perché, mentre parlavamo ho notato che lo spicchio verde di Davide, che in effetti sono la stessa cosa ai due spicchi e mezzo del grafico di Giacomo. Lo spazio verde totale è uguale sia nel grafico di Davide che in quello di Giacomo e così anche per lo spazio azzurro
Ins: qual è o quali sono i metodi che funzionato? Perché?
Davide: è giusto sia il mio metodo che quello di Giacomo
Giacomo: l’unica cosa che cambiava era la semplicità. Se mettiamo a confronto il grafico di Davide e quello di Enea le percentuali sono giuste in tutti e due i grafici. Quello di Enea ha gli spicchi molto più piccoli, quello di Davide ha pochi spicchi più grandi
Leon: quello di Edo non andava bene, perché potevi fare il 25% anche solo di un quadretto e non andava bene. Perché non è davvero il 25%
Ins: quindi confrontando i due metodi che funzionano cos’hanno in comune? Cosa, invece, cambia?
Giulia: secondo me gli spicchi
Ins: in che senso?
Enea: secondo me l’unica differenza è la semplicità. Perché quello di Giacomo dovevi pensarci di più, quello di Davide era più facile
Davide: secondo me resta uguale che siamo sempre partiti da un cerchio, di diverso c’è il numero degli spicchi, i miei erano più grandi quindi ne ho fatti di meno, Giacomo ne ha fatti di più ma sono più piccoli. Però di uguale c’è che in tutti e due la parte verde rappresenta il 25% e quella blu il 75%, anche se il numero di spicchi è diverso.
30 marzo 2021
Costruire un grafico a torta qualsiasi
Ho raccolto tutti i grafici tramite Classroom e abbiamo iniziato a messaggiare sulla piattaforma rispetto ai ragionamenti fatti per arrivare a costruire il grafico a torta. Ne ho selezionati alcuni per illustrarli a tutta la classe, al fine di individuare una regola funzionale a costruire un grafico a torta con percentuali di qualsiasi tipo. Quel pomeriggio la linea non funzionava un granché quindi abbiano analizzato solo un numero limitato di grafici da me precedentemente selezionati.
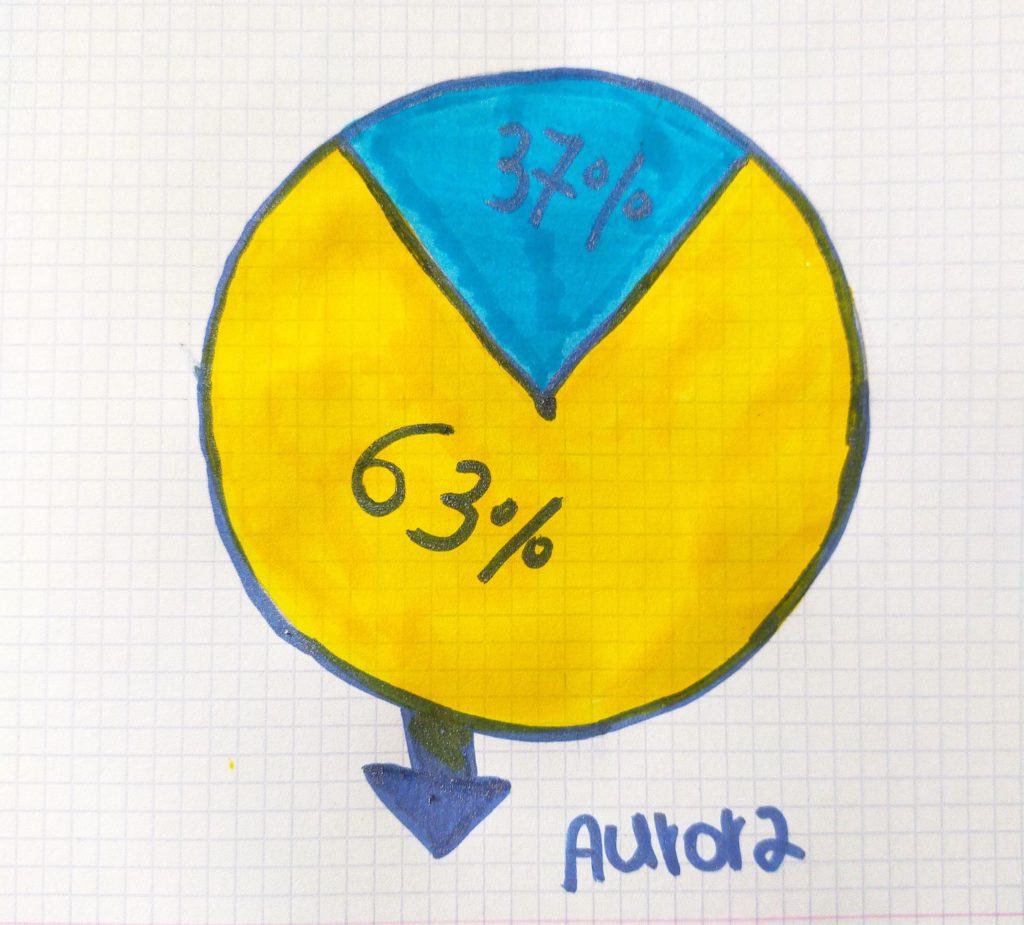
Aurora: ho provato a contare i quadretti per fare 37%, ho provato a riempire lo spicchio mettendoci dentro 37 quadretti.
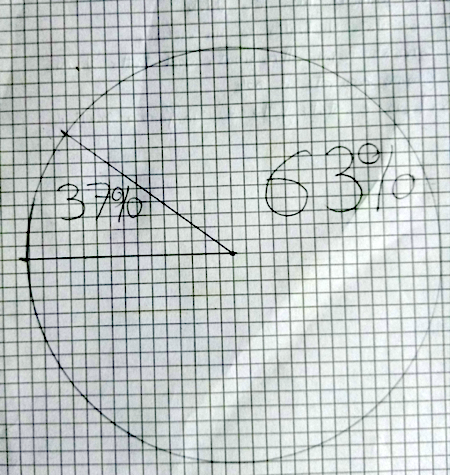
Leo C: ho fatto un cerchio, poi ho contato 37% come se fossero i 37° del goniometro. Lo spicchio del 63% era tutto il resto.
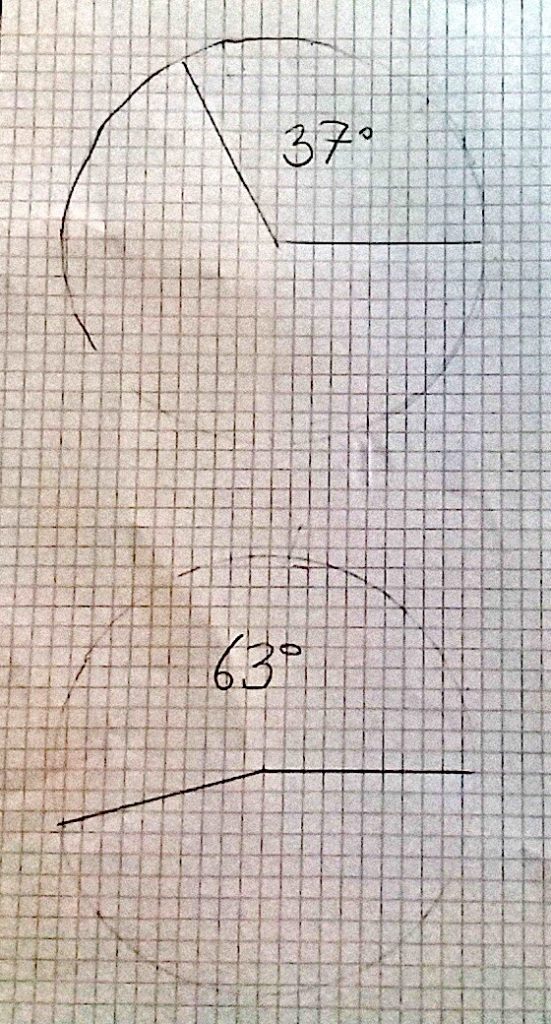
Giacomo: mi sono accorto che ho sbagliato perché già qui ho fatto due grafici al posto di uno. Io ho calcolato che sul goniometro se ¼ è 90°, allora 100:4 fa 25, quindi ogni quarto è 25°.
Ins: prova a spiegare meglio il ragionamento che hai fatto, perché dici che ¼ ha ampiezza di 25°?
Giacomo: Il cerchio corrisponde a 100% quindi 360°, quindi ¼ corrisponde a 25° perché è ¼ su 100.
Ins: tutti d’accordo?
Enea: il ragionamento non è del tutto corretto. Ma non lo so spiegare
Martino: non è 25°, perché ¼ corrisponde a 90°
Giacomo: in effetti mi sono confuso, io stavo pensando a 25%, quindi però non capisco come si fa a raggiungere 37% se ¼ corrisponde a 90°. Sicuramente dev’essere maggiore di 90°
Ins: esatto, quanto di più?
Giacomo: io ho fatto 25% ovvero 90° più 12° che erano quelli che mi mancavano.
Ins: mancano 12° o manca il 12%?
Enea: manca il 12% non 12°
Giacomo: io mi sono confuso, ho confuso gradi e percentuali, perché 12% non vuol dire 12°
Reby: io ho calcolato il 63% in gradi
Ins: come si fa?
Reby: ho fatto 63% di 360°
Ins: perché?
Reby: perché in tutto il 100% è 360°, è un angolo giro
Ins: siete d’accordo con Reby?
Enry: io sono d’accordo
Enea: io sono abbastanza d’accorto, il metodo mi sembra corretto. Ma io l’ho fatto in un altro modo
Ins: vediamo se avete usato un altro metodo oppure no
Enry: io ho fatto 37% + 63% fa 100% ovvero un angolo giro 360°, perciò ho fatto 360°:100 per sapere quanto vale uno dei 100 spicchi. Fa 3,60. Quindi 3,6 sarebbero i gradi di uno spicchio su 100. Poi ho fatto 3,6 x 37 perché così capisco quanti gradi sono ampi 37 spicchietti su 100 e fa 133° circa. Quindi 37% è ampio 133,2° ma ho approssimato per difetto a 133°. Poi il 63% è lo spicchio rimanente: quindi 226,8° ma ho approssimato a 227°.
Ins: questo metodo è uguale o diverso da quello di Reby?
Enry: forse è lo stesso
Reby: io ho fatto 63% di 360.
Enea: ha fatto 63/100 di 360
Reby: si fa 360:100 e poi per 63. Quindi io ed Enry abbiamo usato lo stesso metodo.
Enea: anche io ho ragionato come loro


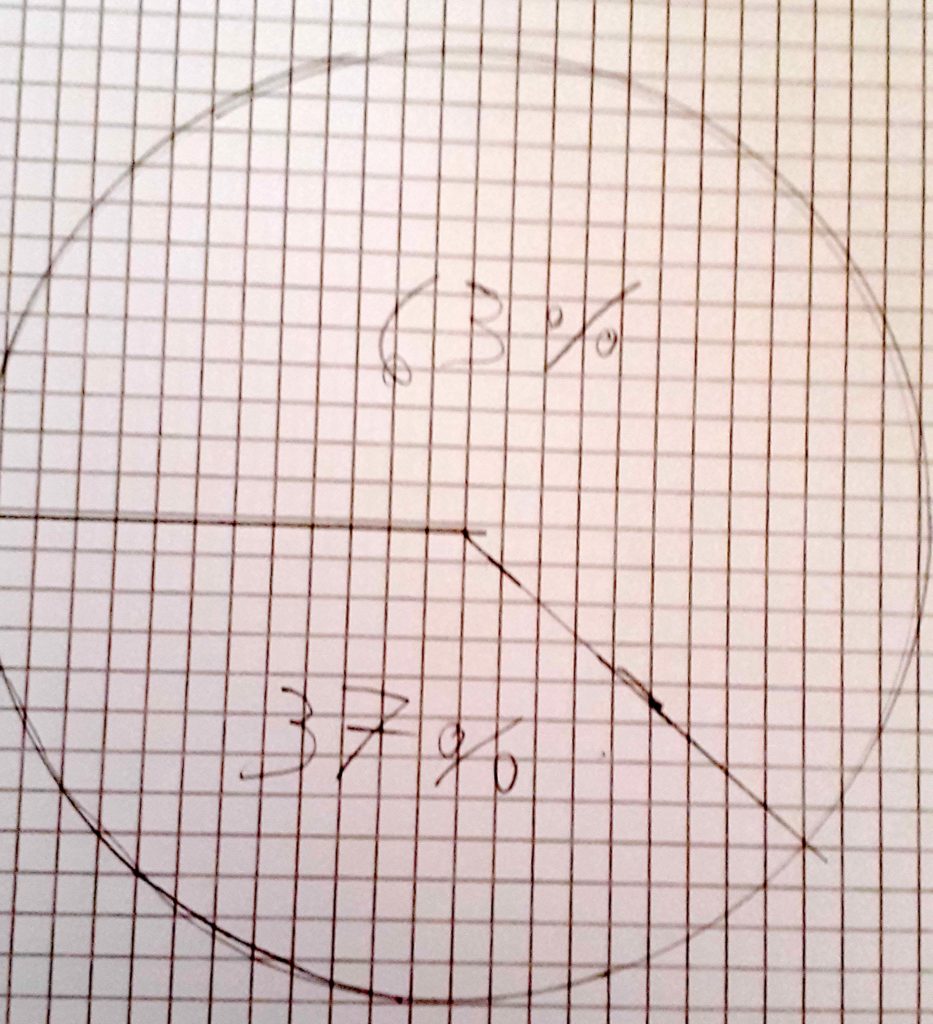

Lulù: io prima ho diviso a metà il grafico così avevo metà, ovvero 50%. Poi ho diviso una delle due metà ancora a metà. Ho trovato il 25%, ora ho 3 spicchi, uno da 50% e due da 25%. Poi ho contato in uno spicchio del 25% quanto mi manca per arrivare a 33 %: mi manca 8%. Così dal 25% ho fatto un segnetto e ho preso il goniometro e ho guardato quanto mi mancava. (Lulù e altri compagni hanno invertito le percentuali che avevo richiesto)
Ins: come?
Lulù: forse dovevo contare i quadrettini
Ins: siete d’accordo con Lulù?
Davide: io no, perché è lo stesso errore di Giacomo
Lulù: mi sono confusa come Giacomo, mi mancava 8%, non 8°. Ho sbagliato. Per sistemarlo posso usare il metodo di Enry che secondo me è corretto.
Ins: bene, confrontandoci insieme ci siamo accorti che è importante non confondere l’ampiezza degli spicchi con la percentuale da rappresentare, grazie agli errori di Giacomo e di Lulù abbiamo capito che 25% non corrisponde a 25°, e nemmeno 8% corrisponde ad un’ampiezza di 8°. Ma possiamo identificare una regola generale per rappresentare percentuali qualsiasi su un grafico a torta?
Davide: secondo me sì, è un po’ la regola che hanno usato Enrico, Enea e Rebecca e anche io. Bisogna dividere l’intero per 100 e poi moltiplicare per la percentuale che ci serve.
Lulù: se il cerchio è sempre un angolo giro quindi 360° allora 1% è sempre ampio 3,6°, il grafico a torta è sempre lo stesso. Cambia la percentuale da rappresentare
Ins: quindi ad esempio se volessi rappresentare la percentuale 55%?
Filippo: metà intero sono 180° più l’ampiezza di 5%
Martino: quindi 50% 180° poi sommiamo i gradi del 5%
Davide: dobbiamo fare 180° più 3,6° x 5
Martino: si perché allora, tu sai che metà intero sono 180°, lo sai perché è proprio un angolo piatto ma potresti anche calcolarlo. Poi come ha detto Lulù 1% è ampio 3,6° perché abbiamo fatto 360°:100. Poi dato che la percentuale che ci manca è 5% basta fare 3,6°x 5 come ha detto Davide e trovi che 55% è ampio 198°, mentre parlavate ha fatto 3,6×5 che fa 18 e poi l’ho sommato a 180.
Ins: bravissimi avete trovato la regola generale per rappresentare percentuali qualsiasi su un grafico a torta. Alcuni di voi avevano già individuato questa regola e l’hanno usata per rappresentare il grafico richiesto 37% e 63% altri invece ci sono arrivati ora discutendo insieme. Come avrete notato anche gli errori ci hanno aiutato a capire meglio cosa fare e come farlo. Ben fatto ragazzi, ora, chi si è accorto di aver realizzato un grafico a torta sbagliato lo corregga per la prossima volta.

Davide ha ragionato sulle percentuali ma solo nella discussione insieme si è accorto di essersi confuso, il 13% mancate è stato rappresentato con ampiezza 13°, durante la discussione però spiega il ragionamento il modo corretto.


Edoardo ha rappresentato due percentuali non richieste 33% e 67% utilizzando un ragionamento funzionale e corretto.
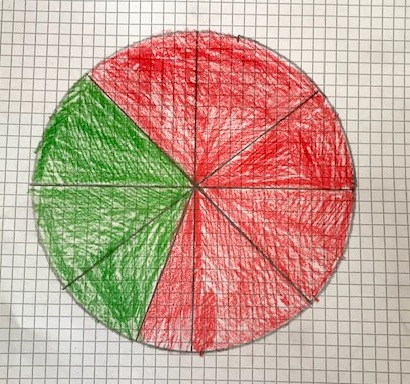

Filippo e Leo I. ragionano diversamente: dividono l’intero a metà e poi ognuno dei 2 spicchi viene diviso ulteriormente a metà. Filippo divide gli spicchi da 25% ancora a metà. Durante la video lezione non c’è stato il tempo di sentire il loro punto di vista. Mi ero ripromessa di riprendere il discorso subito dopo le vacanze di Pasqua ma poi mi sono fatta prendere da altro, mea culpa. Sarebbe interessante sentire cosa dicono gli altri a riguardo, dato che in questo caso non è stato rappresentato uno spicchio con valore 37% ma con valore 37,5%. Sicuramente la scelta delle percentuali da me selezionate non è stata delle migliori perché si poteva facilmente cadere nell’inganno che bastasse prendere uno spicchio da 25% e metà di uno spicchio da 25%

Giulia commette lo stesso errore fatto anche da altri e discusso in video lezione: 36% non corrisponde a 36°, durante la lezione su Meet però non è intervenuta per problemi di audio.
altra data da cercare
ANALIZZIAMO I GRAFICI A TORTA SUL LIBRO DI GEOGRAFIA
Ins: Buongiorno bambini oggi continuiamo il nostro lavoro sui grafici. È un po’ che non ci lavoriamo ma spero che non vi siate dimenticati tutto il percorso fatto insieme. Vi ricordate che cosa ha dato inizio al nostro lavoro sui grafici?
Edo: siamo partiti dalla creazione di Gabriel
Ins: esatto, siamo partiti dalla creazione matematica di Gabriel che ci ha portato a fare un lungo ragionamento sulle percentuali e sui grafici a torta.
Giacomo: comunque posso dire una cosa, la creazione di Gabriel ha aperto un mondo.
Ins: hai proprio ragione, la creazione di Gabriel ci ha dato l’occasione per consolidare cose che già un po’ sapevamo ma anche e soprattutto di imparare cose nuove grazie ai vostri interventi e alle vostre intuizioni. Per oggi vi ho chiesto di portare il libro di geografia. In che modo il libro di geografia ci può aiutare a proseguire il nostro lavoro?
Filippo: nel libro di geografia ci sono tantissimi grafici
Ins: di che tipologia?
Gabriel: nel nostro libro, per ogni regione ci sono 2 grafici a torta. Uno sul territorio e l’altro sui settori economici.
Ins: andiamo a vedere nello specifico come sono realizzati i grafici sul vostro libro. Andiamo a Pag 26 e osserviamo con attenzione il grafico presente nella pagina.
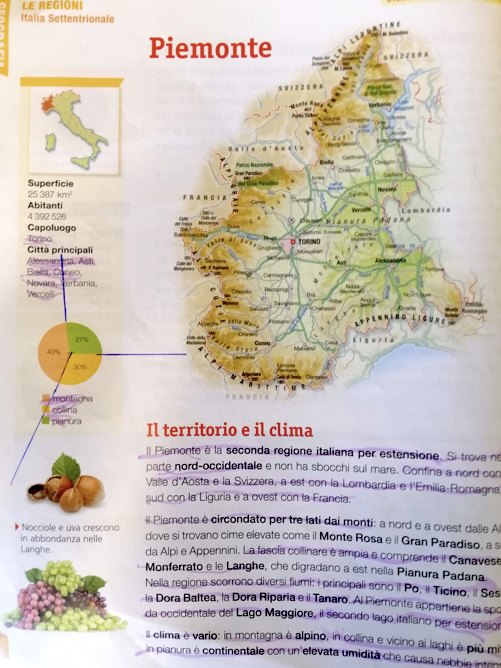
Martino: è il grafico sul Piemonte
Ins: quali informazioni ci fornisce il grafico? Quali informazioni possiamo ricavare osservando il grafico? Senza leggere quello che c’è scritto in questa pagina, riusciamo a capire qualcosa sul Piemonte?
Aurora: si, dice la percentuale di quanta montagna c’è, quanta collina c’è e quanta pianura c’è.
Ins: ok però se lo spieghi in questo modo non si capisce che cosa c’è di uguale o di diverso tra il grafico a torta del Piemonte e quello della Liguria, nella pagina dopo. Possiamo ricavare informazioni più specifiche che, ad esempio, si riferiscono solo ad uno dei due grafici?
Lulù: mi dice le percentuali di pianura, collina e montagna.
Ins: certo, questo però è ciò che ha detto anche Aurora. Proviamo ad essere più chiari, entriamo nello specifico. Prova a pensare di essere una geografa importante, hai questo grafico e devi scrivere una relazione sul Piemonte. Cosa scriveresti?
Lulù: scriverei che la montagna prevale, c’è poca pianura
Martino: poca più o meno
Ins: Martino tu saresti più preciso? Cosa diresti?
Martino: io direi che il territorio del Piemonte è principalmente montuoso, perché dal grafico lo vedi subito ad occhio che la parte marrone è quella più grande e poi lo sai che 43% è più grande di 27% e 30%. Poi non sono tanto d’accordo con Lulù. Non è vero che c’è pochissima pianura. Anzi collina e pianura sono quasi uguali. La collina è un po’ più vasta della pianura ma non di molto. Il 3% in più, non è tantissimo in più.
Ins: le osservazioni di Martino mi sembrano molto precise, bravo. Avete visto quante informazioni abbiamo ricavato solo osservando un grafico. Senza aver letto le pagine del libro sul Piemonte, abbiamo già ricavato delle informazioni sul suo territorio. Ben fatto. Ora però vogliamo anche capire com’è stato costruito il grafico che state osservando. Vi lascio un po’ di tempo per confrontavi a coppie, poi scrivere sul Q. se secondo voi è stato realizzato correttamente oppure no, e poi specificate le vostre motivazioni. Dopo ci confronteremo in una discussione comune.
Enea: io non ho capito
Davide: devi cercare di capire se questo grafico indica le percentuali giuste oppure no.
Alice: dobbiamo guardare se è stato costruito con un’angolazione precisa
Davide: non angolazione, devi guardare la percentuale
Enrico: io penso che bisogna capire quanto vale 1
Ins: 1 cosa?
Enrico: devo prima capire quanto vale 1% del grafico così capiamo se il 27 poi è costruito bene
Davide: bisogna calcolare 1% della superfice, perché ad esempio qui tutte le percentuali sono riferite alla superfice del territorio del Piemonte
Ins: si certo, queste percentuali si riferiscono alla superfice della regione Piemonte che sarebbe?
Edo: 25387 chilometri quadrati
Ins: certo, il 43%, 27% e 30% si riferiscono al totale della superfice del Piemonte che troviamo sul libro.
Edo: nel grafico il 100% rappresenta tutta la superfice del Piemonte, cioè 25387.
Ins: esattamente. E sapendo la superfice totale riusciremmo anche a capire a quanti chilometri quadrati corrisponde la superfice montana, collinare e pianeggiante, e potremmo anche farlo, sarebbe interessante. La domanda che ho fatto prima, però, era un’altra. Come facciamo ad essere sicuri che il grafico sia stato costruito bene? Che il 43% sia proprio uno spicchio così?
Enea: forse ho capito. Guardando il grafico bisogna riuscire a trovare 1% in gradi e poi sommarlo tante volte, ad esempio sommare i gradi che corrispondono all’1% 27 volte così scopriamo quanto dev’essere ampio lo spicchio del 27% e così via.
Davide: e poi se misuriamo con il goniometro i tre spicchi del grafico sul libro possiamo capire se sono corretti oppure no.
Enrico: si esatto, io volevo dire proprio questo. Solo che io non farei il più, farei il per perché è più semplice e veloce
Ins: ok provate con uno dei metodi proposti dai vostri compagni e poi ci confrontiamo
Ho lasciato una ventina di minuti al fine di lasciare il tempo a tutti di comprendere e sperimentare l’ipotesi dei compagni.
Ins: Giulia, tu hai lavorato con Enea. Come avete portato avanti il lavoro per capire se il grafico è corretto o meno?
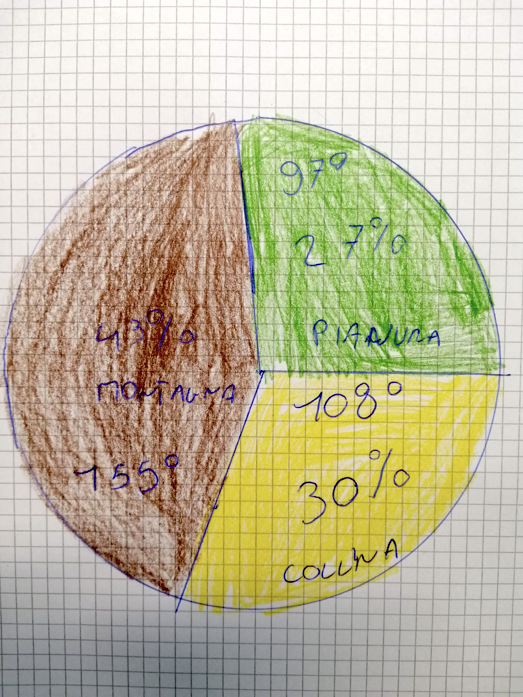
Giulia: noi abbiamo capito che il grafico sul libro non è corretto perché il 27% è 95° invece dovrebbe essere di più di 95°
Giacomo: io ho pensato che il grafico del libro è giusto perché ho pensato che 27% è un po’ di più di 25%. Ho diviso il grafico in 4 parti uguali per fare 4 spicchi da 25% e ho visto che lo spicchio del 27% era leggermente più grande di quello del 25% e ho pensato che poteva andare bene.
Ins: la tua osservazione è corretta, ma noi vogliamo essere molto precisi. Con il tuo ragionamento facciamo un po’ ad occhio. Lo spicchio da 25% quanti gradi è ampio?
Giacomo: 90°
Ins: quindi lo spicchio del 27% a quanti gradi potrebbe corrispondere come ampiezza?
Giacomo: bè ci aspettiamo che sia più di 90°, non lo so, un pochino di più di 90°
Ins: e si però noi che siamo matematici precisi, vogliamo sapere con esattezza quanti gradi in più di 90°, non ci basta dire un po’ più di 90°
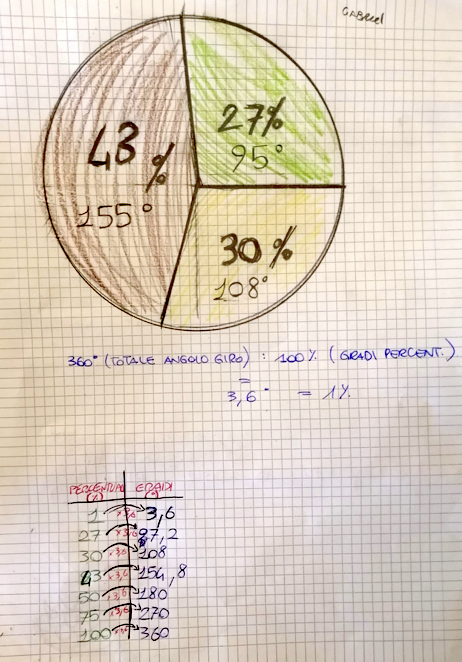
Davide: Noi abbiamo fatto 3,6° x 27 e ci è venuto 97,2. Lo spicchio del 27% dovrebbe essere ampio 97,2°. Questa ampiezza è precisa
Enea: si perché 1% è ampio 3,6°. Abbiamo fatto 360 : 100 perché tutto il cerchio è un angolo giro
Ins: per evitare di confondere i gradi con le percentuali possiamo costruire una tabella: sulla prima colonna mettiamo le percentuali e sulla seconda?
Filippo: sulla seconda mettiamo i gradi. Ad esempio se sulla colonna delle percentuali mettiamo 1 su quella dei gradi dobbiamo mettere 3,6 perché come ha detto Enea 1% è ampio 3,6°
Ins: esatto. Bravi. Notiamo proprio che più aumenta la percentuale da rappresentare e più aumenta l’ampiezza degli spicchi che la rappresentano. Ma come troviamo sul goniometro 97,2°?
Davide: si poteva fare anche l’ampiezza del 25% cioè 90° poi fai più 3,6° e poi ancora più 3,6° e ti viene comunque giusto. Perché ogni 1% in più aumenta sempre di 3.6°
Ins: si certo, perché all’ampiezza del 25% hai aggiunti i gradi che corrispondono all’ampiezza del 2% che sono quelli mancanti per arrivare a 27% e in totale hai l’ampiezza dello spicchio del 27%
Leo C: viene 97,2°
Giulia: però noi abbiamo approssimato a 97° perché non sapevamo come fare 97,2°
Ins: Ottima soluzione, bravi.
Gabriel: sul libro era ampio 95° quindi non è giustissimo
Ins: ora andiamo a controllare anche gli altri due spicchi
Alice M: lo spicchio del 30% dovrebbe essere 108° invece sul libro abbiamo visto che è diverso
Davide: a me sembra che quello sul libro sia 110°
Martino: anche a me
Filippo: quello della montagna è 43 x 3,6° fa 154,8
Edo: quindi approssimiamo per eccesso a 155°
Filippo: sul libro invece è circa 154°
Ins: ok ora abbiamo le ampiezze corrette delle tre percentuali. Proviamo a sommare le tre ampiezze che abbiamo trovato che corrispondono ciascuna a 97° per il 43%, 108° per il 30% e 155° per il 43%. Cosa ci aspettiamo che esca come risultato?
Leo C.: ci aspettiamo che faccia 360°
Jacopo: viene giusto 97+108+155 fa 360
Ins: e se invece sommiamo i valori in gradi che abbiamo rivelato sul libro?
Giacomo: 95+110+154 fa 359 e si capisce già così che non è corretto perché la somma dei gradi totali non è 360°, invece un angolo giro è sempre 360°.
Ins: secondo voi perché il grafico sul libro non è corretto?
Martino: magari perché non pensavano che noi avremmo guardato, invece siamo intelligenti
Enrico: l’hanno fatto un po’ impreciso perché comune si capisce che la montagna prevale su collina e pianura e poi è difficile farlo giustissimo
Giacomo: secondo me l’hanno fatto un po’ impreciso perché è geografia, non matematica
Enea: secondo me perché magari loro l’hanno fatto al computer. Noi però abbiamo visto che si può fare anche con il goniometro facendo qualche approssimazione.
Ins: esattamente, noi abbiamo fatto delle approssimazioni per realizzare il grafico sul nostro quaderno e probabilmente anche le ampiezze dei tre spicchi del grafico sul libro le abbiamo misurate approssimando un po’, perché ci siamo accorti che sul goniometro ci sono solo i gradi interi e ad esempio non potevamo rappresentare uno spicchio con ampiezza 97,2° e abbiamo approssimato a 97°.



QUALI INFORMAZIONI SI POSSONO RICAVARE DA UN GRAFICO A TORTA
Durante la lezione ho proiettato alla LIM il seguente grafico e chiesto loro quali situazioni avrebbe potuto rappresentare un grafico del genere
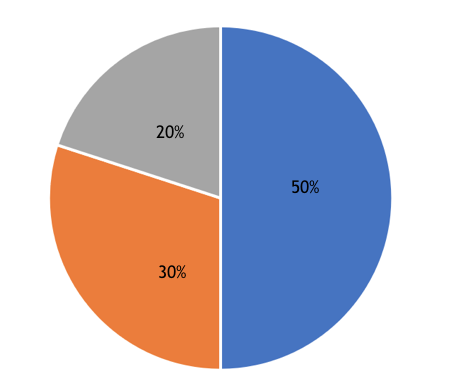
Aurora: per me potrebbe dire che il 50% è lo spicchio maggiore perché c’è più montagna
Ins: ma guardando questo grafico riesci a capire l’argomento preciso da cui è stato tratto?
Lulù: No, non si capisce se il 50% si riferisce alla montagna il 30% alla collina e il 20% alla pianura. Questo non lo stesso grafico dell’altra volta. Questo potrebbe rappresentare una situazione qualsiasi. Ad esempio 50% delle matite sono blu, il 30% rosse e il 20% sono gialle.
Vincenzo: ad esempio ci sono 50 caramelle e le devi dare a 30 bambini
Ins: la situazione di Vincenzo potrebbe essere rappresentata da questo grafico?
Giacomo: secondo me no. Nel caso di Vincenzo basta fare 50: 30 e capisci quante caramelle dare a ogni bambino ma secondo me non c’entra con il grafico. Questo grafico si riferisce a un totale di cose, tipo tu hai un tot di cose e sai che del totale il 50% sono ti un tipo, il 20% di un altro e il 30% di un altro ancora.
Ins: prova a fare un esempio concreto
Giacomo: tipo c’è una torta e Mario ne mangia 50%, Giulia il 30% e Edoardo 20%
Leo C: questo va bene, oppure un po’ come diceva Vincenzo ci sono il 50% delle caramelle del totale alla fragola, il 30% al limone e il 20% ala ciliegia
Filippo: oppure in una città c’è un certo numero di case, il 50% sono marroni, il 30% rosse e il 20% gialle
Aurora: oppure Elisa ha un telefono che è al 50% di batteria, il cellulare di Maria è al 20% e poi Giulia ha il cellulare al 30%
Ins: secondo voi la situazione che ha appena descritto Aurora potrebbe essere rappresentata da un grafico come questo? Si, no perché?
Davide: si
Filippo: secondo me no perché le persone sono solo 3, invece si sta parlando di tante cose. Secondo me non va bene, perché sta parlando della batteria
Ins: ok, pero la tua spiegazione non è molto chiara. Prova a spiegarti meglio
Filippo: non lo so. Secondo me non va bene ma non so spiegarlo
Alice D: secondo me no, perché è vero che la batteria del telefono è espressa in percentuale, tipo sul mio cellulare vedo la carica di batteria che è scritta in percentuale. Tipo se è al 9% capisco che devo metterlo in carica altrimenti poi si spegne. Però non può essere espressa da un grafico a torta così. Nel senso che un grafico delle percentuali indica quanto di queste cose…ad esempio se prendo un barattolo di penne di 3 colori, posso sapere come sono distribuite nei tre colori e dire le 3 percentuali. Posso dire ci sono un tot di penne viola, un tot blu e un tot gialle e posso esprimerlo in percentuale.
Ins: esatto, nella situazione che hai appena descritto c’è una quantità totale che è suddivisa in tre sottogruppi e volendo possiamo esprimere in percentuale la quantità di penne di ciascun colore facendo sempre riferimento al numero di penne iniziale, che sono il nostro riferimento. Invece, nella situazione descritta da Aurora c’è una situazione di riferimento? Un totale a cui riferirci come nella situazione di Alice?
Davide: no perché i cellulari sono 3 diversi, non uno unico
Giacomo: questa cosa l’aveva già un po’ detta Filippo, perché non dico che lui ha detto che erano 3 situazioni diverse, però aveva detto una cosa simile
Ins: si Filippo si stava avvicinando ma poi si è un po’ bloccato con la spiegazione
Giacomo: lui lo trovava sbagliato perché sono 3 situazioni diverse. Ad esempio, io farei tre grafici diversi: uno per il cellulare di Maria che è carico al 50% e colorerei metà verde per indicare la carica e l’altra metà rosso per indicare la percentuale di batteria che si è scaricata. Per l’altra ragazza un altro grafico con il 20% colorato di verde e il resto rosso e per la terza un altro grafico ancora dove coloro 30% di verde e il resto rosso.
Ins: Bene, la situazione di Aurora potrebbe essere rappresentata da 3 grafici diversi come hai spiegato in modo chiaro tu. Proprio perché sono 3 batterie diverse e non possono essere rappresentare da un unico grafico
Martino: maestra io ho un’altra situazione: in una scuola ci sono 100 bambini ad esempio. Il 50% sono maschi, il 30% sono femmine e il 20% sono insegnanti.
Ins: questa situazione potrebbe andare bene?
Giacomo: ma secondo me no, perché gli insegnanti potrebbero essere o maschi o femmine, I maestri possono entrare in due categorie: ad esempio un maestro maschio potrebbe essere messo nella categoria maschio ma anche categoria maestro e non si capirebbe più nulla
Ins: e già, bisogna state attenti perché non possiamo mettere lo stesso dato in due categorie diverse. Se vogliamo capire la percentuale di maschi e femmine in una scuola, in quanti spicchi dovremmo dividere il grafico?
Davide: in due spicchi, uno che indica la percentuale delle femmine sul totale e l’altro spicchio che indica la percentuale dei maschi
Gabriel: magari martino avrebbe potuto dire che nella scuola il 50% sono alunni, il 30% maestri e il 20% bidelle. Perché hai il totale delle persone nella scuola divisi in tre gruppetti
Ins: si questa situazione è perfetta. Magari sarebbe anche utile da inserire sul sito della scuola. Molto bene. Avete fatto molti esempi, che cosa abbiamo capito?
Davide: che un grafico può rappresentare tantissime situazioni. Tipo dal grafico che è ella lim abbiamo raccontato diverse cose. Alcune erano sbagliate ma va bè
Ins: esatto, il grafico, da solo, potrebbe rappresentare moltissime situazioni anche molto diverse tra loro. Dalle situazioni sbagliate, che avete tirato fuori, abbiamo capito cose in più, ovvero che bisogna avere un’unica situazione si riferimento e un totale di cose da suddividere in sottogruppi che possiamo poi esprimere in percentuale rispetto al totale. Cos’è che ci aiuta a capire cosa può dirci un grafico?
Lulù: la legenda. Tipo sul grafico che era nel libro di geografia abbiamo capito subito che era sul territorio perché c’erano i colori che ci davano delle informazioni tipo arancione era la montagna, giallo la collina e verde la pianura. Senza la legenda non si capiva bene se era sul territorio oppure sui settori economici. Anche il titolo del grafico ti aiuta a capire di cosa parla.
Ins: proprio così. Un grafico da solo, senza legenda, può riferirsi ad una quantità infinta di situazioni. La legenda ci aiuta a capire l’argomento e soprattutto a come leggere il grafico. Ma per rappresentare le diverse situazioni esiste solo il grafico a torta oppure ci sono altri modi per rappresentare le informazioni?
Gabriel: no ad esempi quando abbiamo fatto l’indagine sulla temperatura abbiamo rappresentato i dati su un piano cartesiano, da una parte mettevano i giorni del mese e sulla colonna mettevamo i gradi della temperatura e poi mettevamo dei punti che ti dicevano quel giorno che temperatura c’era.
Davide: e poi c’è anche l’istogramma, che si fa tipo con delle colonne
Ins: esatto, esistono diversi modi per rappresentare i dati che raccogliamo o una specifica situazione. Ma tutti i grafici vanno bene per rappresentare tutte le situazioni?
Gabriel: no, quello della temperatura non potevamo farlo tipo con il grafico a torta.
Giacomo: però dipende, se ci sono un tot di penne di 3 colori diversi possono rappresentare le percentuali con un grafico a torta oppure anche un istogramma.
Ins: ok quindi alcune situazioni possono essere rappresentare da più grafici, mentre in altri casi no. Facciamo una cosa. Ci dividiamo in gruppetti, ogni gruppo sceglie un argomento su cui fare un’indagine da sottoporre ai compagni e poi provate a rappresentare i dati raccolti con due diversi grafici. Poi provate a spiegare quale dei due grafici costruiti rappresenta meglio la situazione indagata e perché.


17, 18 e 25 maggio 2021
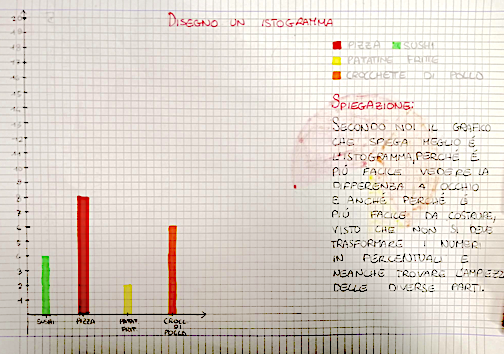
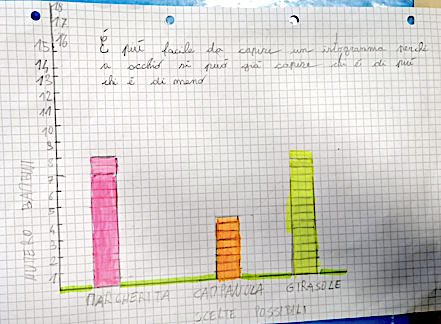
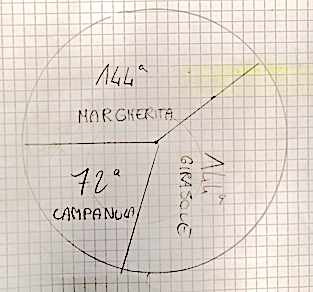
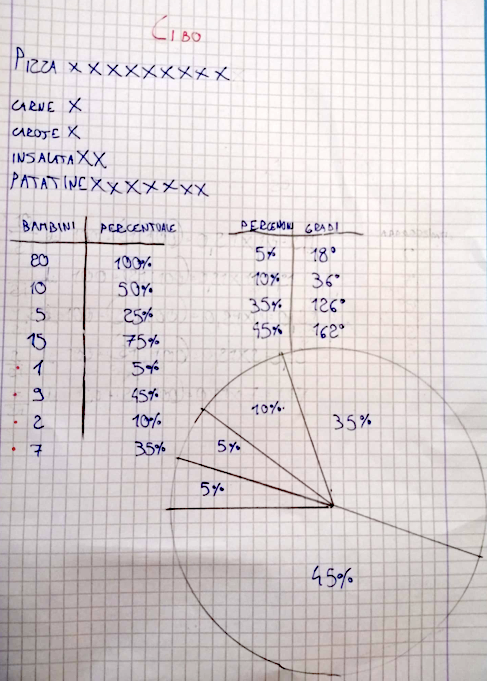
TANTI GRAFICI
Durante la lezione gli alunni hanno avuto modo di presentare il lavoro fatto in piccoli gruppi sulla realizzazione dei due grafici. Complessivamente è emerso che tutte le situazioni indagate dai gruppi potevano essere rappresentare sia con un grafico a torta, sia con un istogramma. Per la maggior parte degli alunni entrambi i grafici spiegano bene le situazioni analizzate, l’istogramma è risultato essere il grafico scelto dalla maggioranza in quanto più semplice da realizzare, sull’istogramma guardando le colonne si riesce subito a capire il numero di bambini inserito in ciascuna delle categorie indicate. Nel grafico a torta no, guardando solo il grafico si può capire qual è la categoria che è stata selezionata maggiormente ma per capire quanti bambini appartengono a ogni categoria bisogna fare dei calcoli.
Vincenzo, Edoardo, Alice

Edo: Per noi è stato complicato costruire il grafico a torta, prima di tutto abbiamo visto quante persone hanno scelto ogni categoria. Ad esempio la pizza è stata scelta da 8 persone su 20. Allora poi abbiamo capito che 4 persone equivalevano al 20% perché 4 x 5 fa 20, quindi poi 8 persone erano 40%, perché era il doppio. Quindi poi 2 persone sono il 10% e così abbiamo capito come trasformare le persone di ogni categoria in percentuali.
Alice: Poi per costruire il grafico a torta abbiamo cercato di capire quanti gradi erano le percentuali. Abbiamo fatto 3,6 per 20 per capire l’ampiezza dello spicchio del 20%
Ins: come avete trovato 3,6? Cos’è?
Alice: è quello che corrisponde a 1 grado
Lulù: ma no, sono i gradi di 1%
Edo: si perché abbiamo fatto 360: 100 e abbiamo trovato 3,6 che è l’ampiezza di 1% poi moltiplicando per 20 che era la percentuale da rappresentare abbiamo trovato l’ampiezza del 20%. Poi abbiamo fatto così anche per le altre.
Ins: bene, ben fatto. Vincenzo, invece come avete costruito l’istogramma?
Vincenzo: abbiamo fatto delle colonne. Tipo per la pizza erano 8 persone quindi abbiamo fatto una colonna che arrivava fino al numero 8
Alice: abbiamo fatto che ogni due quadretti era un bambino. Per noi è stato più facile fare l’istogramma, l’altro era più difficile perché bisognava fate tanti calcoli
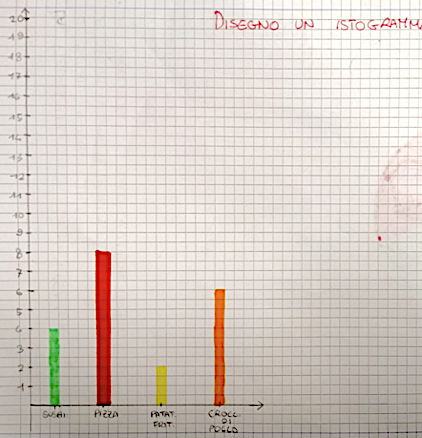
Ins: voi cosa pensate, la situazione descritta da questo gruppo si capisce meglio dal grafico a torta, dall’istogramma o da entrambi e perché?
Leo C: allora dall’istogramma riesco a vedere subito il numero di persone che hanno scelto ogni cosa. Ad esempio se guardo il loro istogramma capisco subito che le patatine fritte l’hanno scelto 2 persone. E capisco subito che la maggioranza ha scelto la pizza. Nel grafico a torta si vedono sono le percentuali
Ins: nel grafico a torta riesci a capire qual è il pasto preferito degli alunni della 5b?
Leo c: si quello rosso è lo spicchio più grande, quello della pizza. Quindi capisco che l’hanno scelto più persone. Però non capisco subito il numero di persone che ha scelto la pizza. C’è scritto 40% ma non vuol dire che 40 persone hanno scelto la pizza.
Ins: e per sapere quanti bambini hanno scelto la pizza guardando solo il grafico a torta?
Leo C. devo fare dei calcoli, se sono che i bambini totali sono 20 devo capire cos’è il 40% dei 20 bambini
Filippo: anche noi abbiamo fatto sul cibo ma non abbiamo fatto l’istogramma, ci siamo dimenticati
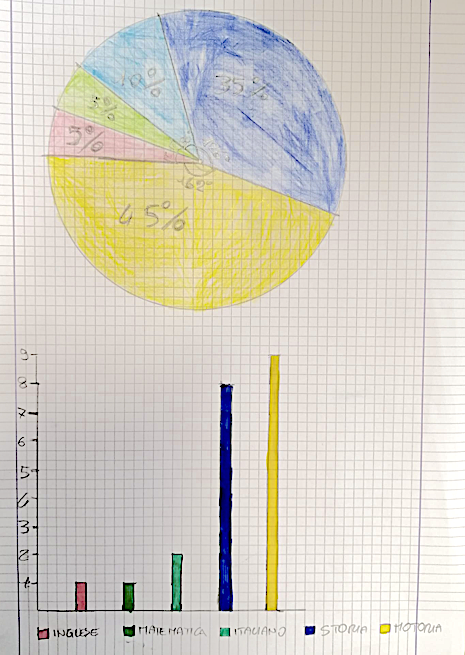
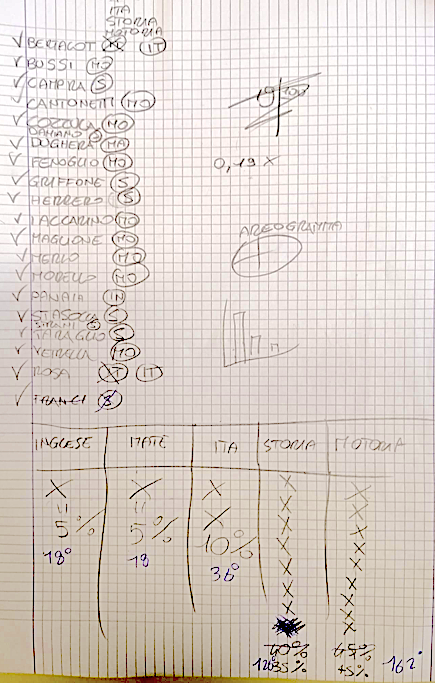
Filippo, Leon, Giulia, Rebecca

Giulia: da noi hanno scelto di più le patatine
Reby: noi abbiamo capito che 9 bambini erano i 45%
Giulia: abbiamo fatto 5 x 9
Ins: e perché avete fatto 5 x 9?
Giulia: 9 erano i bambini e 5 erano: pizza, carote, insalata, carne e patatine
Ins: sei sicura che bisogna moltiplicare per 5 perché 5 erano le categorie della vostra intervista?
Lulù: hanno sbagliato, si fa 3,6 x 9
Ins: sei sicura?
Davide: no quello che dice Lulù serve per capire l’ampiezza degli spicchi per fare il grafico a torta perfetto
Filippo: ora mi sono ricordato, 20 bambini era il 100% perché era il totale e poi….
Cozzula: sappiamo che il 100% sono 20 bambini quindi facciamo 20:100
Filippo: abbiamo fatto per 5 perché 5% corrisponde a 1 bambino. Quindi 9 bambini sono il 45% dell’intero perché 9 x 5 fa 45. E poi per fare il grafico a torta abbiamo fatto 3,6 per 45 come hanno fatto gli altri
(…qui abbiamo fatto una piccola pausa perché è entrata la rappresentante di plesso a fare una comunicazione piuttosto lunga e mi sono accorta di aver un po’ perso il filo del discorso..)
Ins: Quante tipologie di grafici conosciamo?
Lulù: il grafico a torta e l’istogramma
Ins: e basta?
Leo I: anche il piano cartesiano
Ins: quando l’abbiamo usato?
Leo I: quando abbiamo fatto il lavoro a gruppo sulle temperature da un lato mettevano i giorni del mese e dall’altro i gradi della temperatura
Ins: avremmo potuto rappresentare le temperature medie giornaliere del mese di gennaio usando un grafico a torta?
Lulù: no perché non potevano mettere tutte e due le cose
Leo C: magari potevamo fare un grafico a torta sui giorni di pioggia e di sole del mese ma non sulle temperature
Ins: in quale altra occasione abbiamo urato il piano cartesiano come grafico per rappresentare una situazione? Se non vi ricordate andate a guardare sul vostro quaderno
Alice D: abbiamo fatto un piano cartesiano e da un lato abbiamo messo il costo del pane al sesamo e dall’altro i chilogrammi
Ins: cosa andavamo a segnare sul grafico?
Aurora: le tacche dei chilogrammi, tipo ogni tacca era 0,100kg e poi sull’altra gli euro, ogni tacca era cinquanta centesimi
Ins: ok ma poi era finito li oppure abbiamo fatto altro?
Lulù: tipo andavamo a vedere a quanti euro corrispondevano in chilogrammi delle tacchette.
Leon: mettevamo un puntino, poi guardando capivi che tipo 100 grammi di qualcosa costavano un certo prezzo. Più aumenta la quantità che compri e più aumenta il prezzo e lo vedevi bene dal grafico
Ins: che differenza c’è tra un piano cartesiano e un grafico a torta? Quando conviene usare uno piuttosto che l’altro?
Lulù: quando hai più unità di misura
Ins: in che senso?
Davide: perché nel paino cartesiano ci sono i chili e l’euro. Come ha detto Leon se cambia uno, cambia anche l’altro
Ins: esatto, nel piano cartesiano abbiamo due cose che sono in relazione tra loro. In questo caso chili di pane e il relativo prezzo, più aumenta la quantità di pane che compro e più aumenta il prezzo. Ma in che modo il prezzo sale?
Giulia: sale con una certa regolarità
Ins: in che senso? Spiegati meglio
Lulù: il prezzo sale regolarmente, ad esempio 100 grammi costano 50 centesimi, 200 grammi costano 1 euro. Da una tacchetta all’altra dei grammi il prezzo aumentava sempre allo stesso modo
Davide: nel grafico a torta invece hai solo un soggetto, non metti in relazione più cose. Tipo lo puoi fare su una cosa, come abbiamo fatto prima l’argomento era i cibi preferiti dei bambini. L’istogramma invece non ti dice la percentuale, ti fa capire bene il numero di persone in ogni categoria.
Ins :e se invece volessi rappresentare con un grafico una situazione del genere: analizzo i dati relativi agli iscritti delle varie università di Torino divisi in categorie maschi e femmine perché voglio scoprire quali sono i corsi di laurea frequentati principalmente dalle donne e quali invece dagli uomini. Quale grafico utilizzerei per rappresentare i dati raccolti?
Alice D: forse un istogramma o un grafico a torta
Ins: prova a spiegare come costruiresti un grafico a torta, ti ricordo che per ciascun corso di laurea dobbiamo mettere in evidenza gli iscritti uomini e gli iscritti donne
Alice: io lo farei in percentuali. Farei un unico grafico a torta dove metterei le percentuali di maschi e di femmine di tutte le università
Lulù: io fare un istogramma. Metterei le varie università e per ognuna farei due colonne, una per i maschi e una per le femmine. (è venuta alla lavagna e ha rappresentato un istogramma simile a quello che segue, mi sono dimenticata di fare una foto della lavagna)
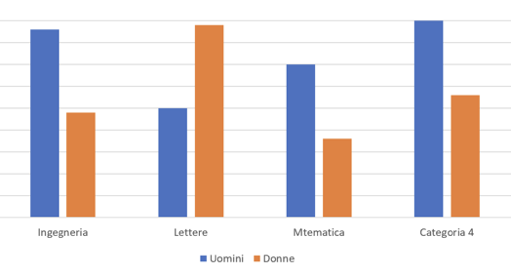
Ins: guardando il grafico di Lulù, riusciamo a capire se ingegneria è frequentata più dai maschi o dalle femmine?
Giulia: si, si capisce bene che sono di più i maschi, perché la colonna blu è più alta
Davide: con il grafico a torta possiamo vedere qual è l’università con più persone, tipo sul totale delle persone iscritte all’università il 50% fa ingegneria ma non si vede la differenza tra maschi e femmine di più università
Ins: esatto, vedete come ogni situazione può essere rappresentata in modi diversi che permettono di capirla osservando con attenzione solo il grafico. Abbiamo visto che alcune situazioni possono essere rappresentare con grafico a torta o istogramma. Costruire un istogramma è più semplice, ma quando abbiamo grandi numeri può essere più comodo un grafico a torta che è più complicato da realizzare, ma abbiamo imparato bene come si fa. Altre volte ancora, invece, dobbiamo usare il paino cartesiano quando c’è una relazione tra due cose: ad esempio grammi di pane e prezzo in euro. È importante saper selezionare la tipologia di grafico più funzionale a descrivere la situazione che si sta analizzando facendo in modo che altri riescano a comprendere l’argomento osservando solo il nostro grafico.
31 maggio 2021
SITUAZIONE PROBLEMA: Il figlio del re e il messaggero
ANALISI PRODOTTI DEGLI ALUNNI SULL’ATTIVITA’ DEL MESSAGGERO
GRUPPO 1: Davide, Aurora, Leonardo C., Leon
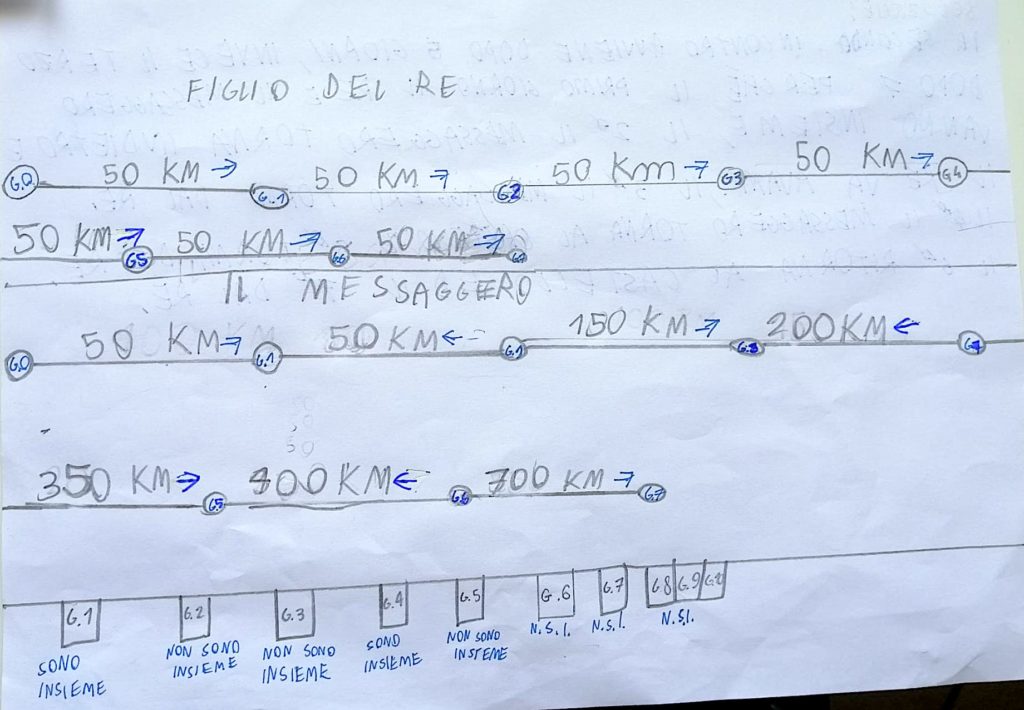

Il gruppo 1 ha compreso che il primo giorno sia il figlio del re, che il messaggero percorrono 50 km. Hanno deciso di rappresentare i percorsi dei due protagonisti con delle frecce per far capire il senso di marcia. Si capisce bene che gli alunni hanno compreso che il figlio del re va sempre in avanti di 50 km al giorno. Risulta più complicato comprendere il percorso del messaggero. Per loro il G0 coincide con il punto in cui si trova il castello. Dalla loro rappresentazione sembra che il primo giorno il messaggero arrivi al 50° km e poi torni indietro al castello. Dal loro schema sembra che Il messaggero faccia i primi 50km con il principe e altri 50km per tornare al castello sempre il primo giorno. Dal loro schema sembra che la prima notte il principe dorme alla tappa 1 e il messaggero al castello. Poi, accanto al giorno 3 scrivono 150km per il messaggero, intendendo che il messaggero deve percorrere 150km per raggiungere il principe e incontrarlo. Dallo schema sembrerebbe che i due si siano incontrati perché poi dal 4° giorno la freccia è in senso opposto, verso il castello per andare a prendere i gioielli. In realtà però per tornare al castello deve percorrere 150 km non 200. Nella spiegazione scrivono che il terzo giorno si incontrano (per la prima volta), nello schema invece hanno scritto che il terno giorno non sono insieme, quindi non è chiaro se hanno compreso che il terzo giorno si incontrano. Per loro, il secondo incontro avviene dopo 5 giorni e il terzo dopo 7 giorni. Non mi è molto chiaro come siano arrivati a questa ipotesi.
GRUPPO 2: Edoardo, Martino, Lulu’
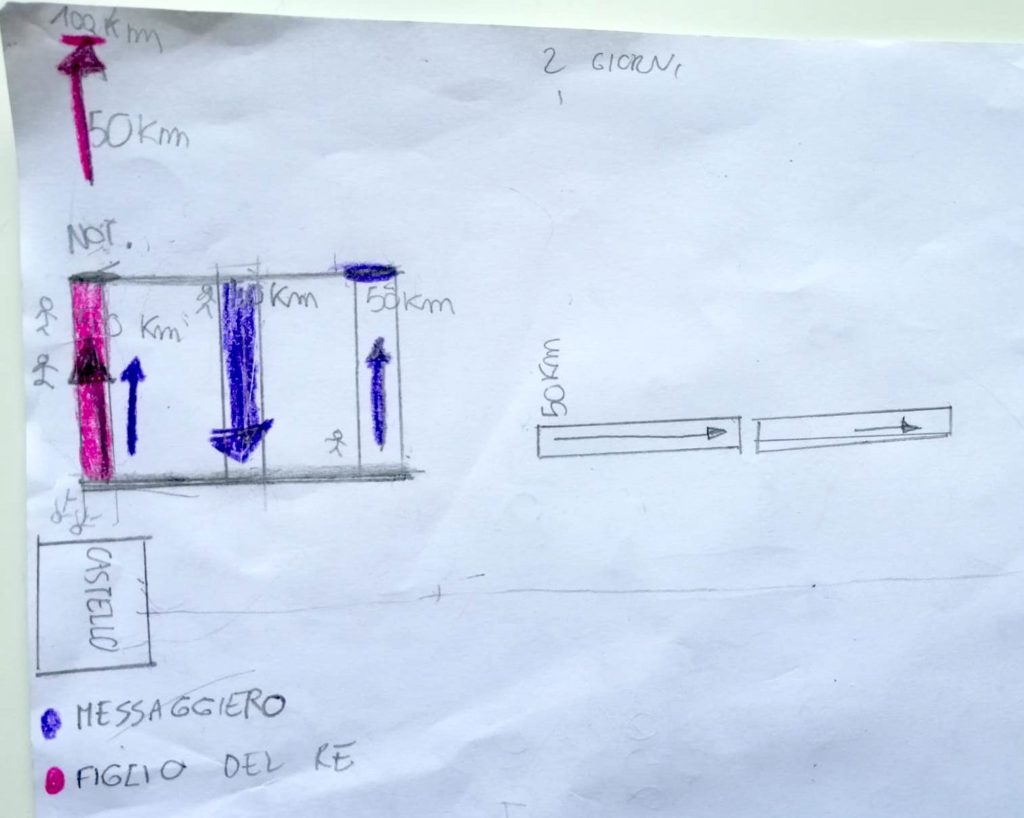
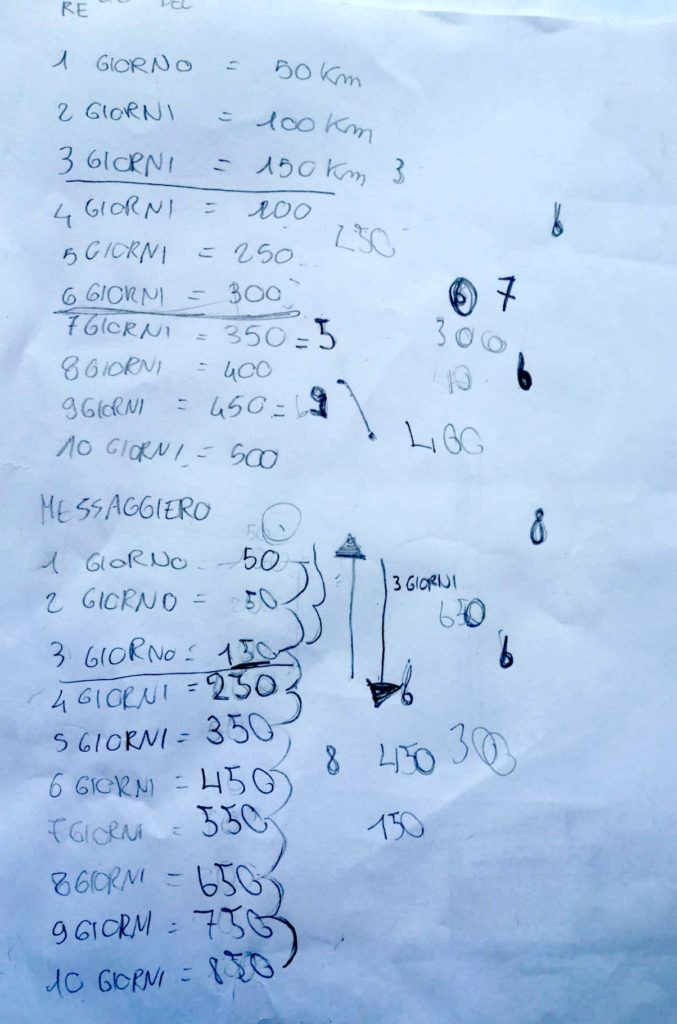
Gli alunni del gruppo due hanno cercato di rappresentare su una tabella i km in cui si trovano i due protagonisti nei vari giorni. La tabella con i km percorsi dal figlio del re è corretta. Le cose si complicano nel completare la tabella relativa ai km in cui si trova il messaggero nei vari giorni. I primi tre giorni sono corretti. Ci sono due frecce in senso opposto che fanno comprendere che gli alunni hanno chiaro il fatto che il cavaliere torni indietro, fino al castello, per poi proseguire in avanti. Ciò si evince soprattutto nel primo schema un po’ abbozzato fatto da Lulù che sosteneva che il messaggero dorme due notti alla tappa 1 (sia la prima che la seconda notte). Dal terzo giorno in poi, non si sono più ricordati che il cavaliere doveva tornare al castello, quindi al posto di sottrarre 100km ai 150 in cui si trovava, ne hanno aggiunti 100, come se il cavaliere continuasse il suo percorso in avanti. Fino al giorno 3 hanno fatto un confronto tra i chilometri in cui si trovavano i due protagonisti, sottolineando il terzo giorno, si trovano allo stesso chilometro (primo incontro), poi si sono un po’ persi perché non hanno fatto tornare indietro il messaggero, ma fatto andare in avanti di 100km al giorno.
GRUPPO 3: Alice D., Gabriel, Giulia, Leonardo I.
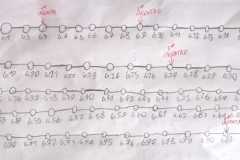
Il terzo gruppo in un primo momento ha cercato di rappresentare la situazione descritta con un disegno. Poi, non riuscendo a proseguire, hanno deciso di cambiare strategia: disegnare tante tappe, ciascuna distante 50km l’una dall’altra (idealmente) e usare due gomme colorate (bianca il figlio del re e blu il messaggero) per capire bene cosa succedeva nei vari giorni. Invio il video con la spiegazione fatta con le gomme, in questo modo sono riusciti a determinare, concretamente dopo quanti giorni avviene il 1° e il 2° incontro.


Video della strategia risolutiva adottata dal gruppo 3
GRUPPO 4: Enea, Filippo, Rebecca
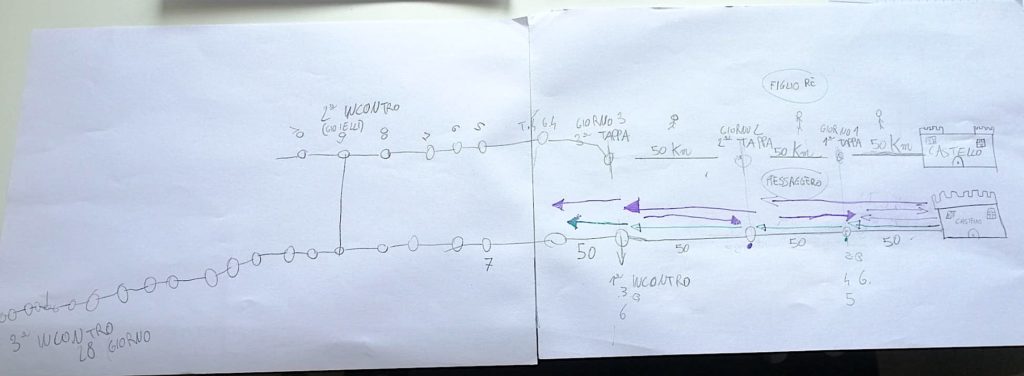
Gli alunni del gruppo 4 hanno compreso che il figlio del re va sempre avanti, frecce verdi, mentre il messaggero, talvolta torna indietro, frecce in due direzioni viola. Hanno compreso che tra una tappa e l’altra ci sono 50km. Anche, in questo caso, si osservano delle difficoltà nel rappresentare le frecce che indicano il percorso del messaggero. Ad esempio le prime due frecce viola, che hanno due direzioni diverse, dalla prima tappa al castello e viceversa, sono corrette. Poi però avrebbero dovuto rappresentare un’altra freccia dalla prima tappa alla terza. La lunghezza delle frecce non è coerente, così come anche la distanza tra una tappa e l’altra. Si intuisce che siano 50 km ogni tappa, ma poi le tappe sembrano avvicinarsi, probabilmente perché il foglio stava per finire. Mi sono accorta che anche questo gruppo ha usato concretamente due oggetti: gomma e temperino per vedere bene gli spostamenti dei due personaggi. Credo che abbiano individuato i giorni del 2° e i 3° incontro in questo secondo modo. Anche se poi i giorni del 3° incontro sono sbagliati, probabilmente perché le varie tappe erano troppo ravvicinate e hanno contato male.
GRUPPO 5: Giacomo, Enrico, Jacopo, Alice M


Nel quinto gruppo, gli studenti hanno deciso di rappresentare la situazione facendo una tabella riportando ogni giorno il numero di chilometri percorsi da ciascun personaggio. Il primo giorno percorrono entrambi 50 km insieme. Il secondo giorno, poiché si dividono, il messaggero percorre 100 km e il principe 50km al giorno. Questo gruppo ha calcolato i chilometri percorsi ma non ne si evince il senso di marcia dei due protagonisti. Hanno cerchiato i chilometri fatti da ciascun personaggio nei giorni in cui si incontrano ma non è chiaro come abbiano capito i giorni in cui si incontrano.
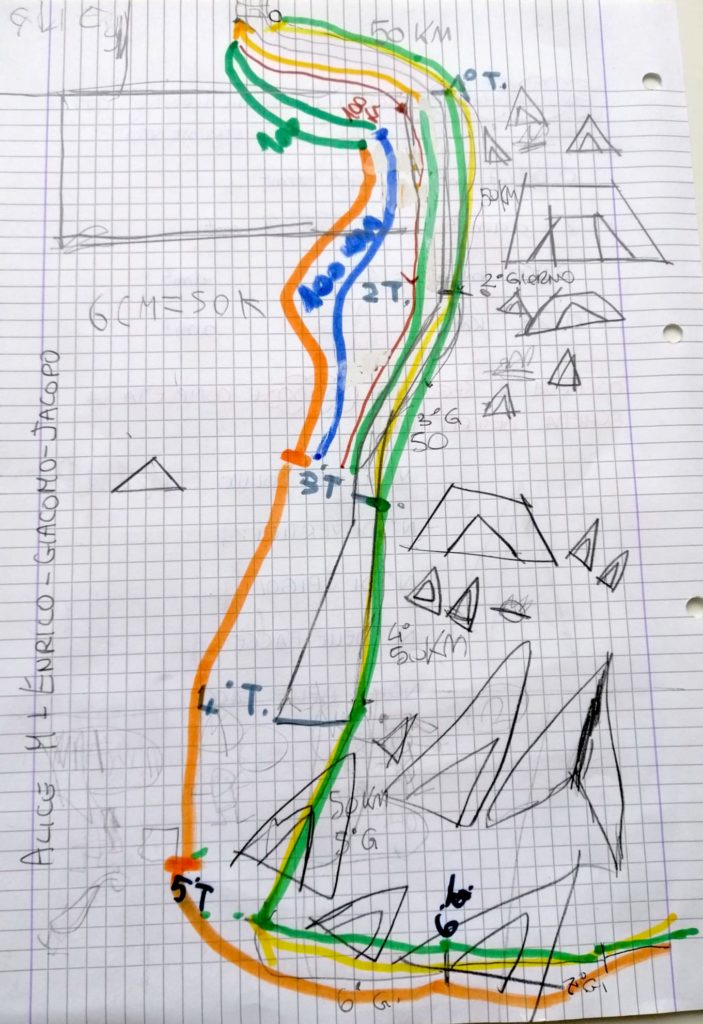
Il disegno è stato rappresentato dall’alunno diversamente abile che faceva parte del gruppo, lui adora disegnare quindi i compagni hanno affidato a lui il compito di disegnare la situazione provando a seguire i ragionamenti fatti principalmente da loro. Dal disegno si evincono le diverse tappe e anche sensi di marcia opposti (freccia gialla che torna indietro).
1 giugno 2021
DRAMMATIZZAZIONE ED ESPOSIZIONE DEI LAVORI DEI 5 GRUPPI
Ho riletto il testo della storia, in modo da riattivare i ragionamenti fatti il giorno precedente e fare una piccola introduzione all’alunno che era assente. Dopo abbiamo discusso su come sarebbe stato possibile fare una scenetta per rappresentare cosa avevamo appena letto
Ins: dopo quanti giorni avviene il primo incontro?
Davide: dopo 3
Ins: esatto, ora per capire bene cosa è successo ai due personaggi nella storia, che abbiamo appena letto, proviamo a fare una scenetta. Di cosa abbiamo bisogno?
Enea: il cavaliere e il figlio del re
Giacomo: magari anche qualcuno che dice cosa devono fare, dove devono andare
Ins: si potrebbe essere utile, potrebbe essere il narratore. E basta?
Leon: anche il re, e tutto il seguito del figlio del re
Ins: si però poi dovremmo muoverci tutti e la classe non è molto grande. Quindi terrei solo il figlio del re e il cavaliere per non confonderci con le troppe persone che si spostano
Filippo: il castello
Ins: si certo, perché è importante capire dove posizionare il castello?
Leo c: perché il messaggero ogni volta torta al castello e poi va dal figlio del re
Ins: solo per questo è importante il castello?
Edo: perché è un punto di riferimento per la storia
Ins: e perché? In che senso?
Lulù: perché altrimenti non potremmo sapere di quanto si allontanano i personaggi, e poi il messaggero deve tornare al castello e dobbiamo sapere dove si trova.
Ins: ok, dove mettiamo il castello?
Filippo: la cattedra potrebbe essere il castello
Ins: quindi, ricapitolando, abbiamo il cartello, ora nomineremo il narratore, il figlio del re e il messaggero. Serve altro?
Leon: servono le diverse tappe
Ins: esattamente, cosa usiamo per fare le tappe e perché sono importanti?
Leon: perché così vediamo dove vanno i personaggi, potrebbero essere i banchi perché sono più o meno distanti uguali
Ins: perché è importante che tra le diverse tappe ci sia la stessa distanza?
Rebecca: perchè dal castello alla prima tappa ci sono 50 km, poi dalla prima alla seconda tappa altri 50 km
Ins: e dalla seconda tappa al castello?
Lulù: 100 km: 50km per la prima più altri 50km
Ins: ma come facciamo a capire in che giorno siamo della storia?
Leo C: ogni giorno il figlio del re fa 50 km, quindi tipo 1° giorno 50 km 1° tappa, secondo giorno altri 50km e arriva alla seconda tappa, terzo giorno altri 50km e arriva alla terza tappa. Ogni 50 km fa un giorno. Quinti tipo se percorre 500km il figlio del re….. sarebbero 10 giorni.
Davide: ogni giorno equivale alla tappa
Ins: quindi per capire in che giorno della storia siamo arrivati a cosa dobbiamo stare attenti?
Davide: ai chilometri che fa il figlio del re
Leo C: perché lui va sempre in avanti
Ins: invece il cavaliere?
Giulia: va un po’ avanti e un po’ indietro
Ins: bene iniziamo con la scenetta. Leon fa il narratore, Vincenzo il figlio del re e Jacopo il messaggero. Iniziamo. Dove sono tutti i personaggi all’inizio?
Leon: sono tutti al castello
Ins: ok, si parte dal castello
Leon: il figlio del re e il messaggero, il primo giorno fanno 50 km e arrivano alla prima tappa. Poi dormono li la prima notte. Poi si svegliano il mattino del giorno 2 e il figlio del re dice al messaggero di tornare al castello a prendere le medicine. Mentre il figlio del re continua ad andare avanti.
Ins: la mattina del secondo giorno partono insieme oppure no?
Leo I: partono insieme ma uno va da una parte e l’altro nell’altra direzione (durante la narrazione i bambini personaggio si spostavano tra le varie tappe-banchi)
Ins: esatto, come avete detto voi il principe continua ad andare avanti, mentre il messaggero torna indietro verso il castello
Gabriel: il principe fa altri 50km e va alla tappa due
Leon: invece il messaggero torna al castello facendo altri 50km
Ins: ma quanti km fa il cavaliere in un giorno?
Leon: 100 km
Ins: quindi la seconda notte dorme al castello o da qualche altra parte?
Lulù: il messaggero impiega mezza giornata per andare al castello a prendere le erbe, poi un’altra mezza giornata per tornare dov’era prima. Quindi dorme la seconda notte dove aveva dormito la prima notte, cioè alla prima tappa.
Ins: Brava. Quindi Aurora, dove dormono i due personaggi la seconda notte?
Aurora: il messaggero alla tappa 1 e il principe alla tappa 2. Quindi non sono insieme
Ins: continuiamo la storia
Leon: il terzo giorno il figlio del re va avanti alla prossima tappa, facendo sempre 50km e arriva alla terza tappa. Il messaggero ne fa 100 e arriva anche lui alla terza tappa
Ins: quindi quando si incontrano la prima volta?
Alice D: dopo 3 giorni
Ins: poi cosa succede?
Leon: il quarto giorno il principe dice al messaggero di tornare al castello a prendere die gioielli per le contesse. Si svegliano al mattino presto il figlio del re va avanti sempre di 50km e va a finire alla 4° tappa, invece il messaggero deve andare indietro e va al castello
Ins: siete tutti sicuri?
Rebecca: no, torna alla tappa 1 perché fa 100 km al giorno
Leon: okok, ho sbagliato, poi il quinto giorno il principe va alla tappa 5. Mentre il messaggero torna al castello, il narratore gli dà le pietre preziose e torna alla tappa 1 per dormire.
Leo C: in realtà il quinto girono il messaggero dovrebbe essere alla tappa 2 non la 1
Ins: siete d’accordo con Leon o con Leo C
Leon: no maestra, ho ragione io. Allora se lui è alla tappa 3, fa 100km e arriva alla tappa 1 perché ogni tappa sono 50km poi il giorno successivo (il quinto) va al castello e torna alla tappa 1 50+50 e sono altri 100km
Leo C: sisi okok ho capito
Ins: Leon come fai a tenere bene il conto dei giorni che passano
Leon: guardo il cartellino delle tappe. Se vedo che il principe, che va sempre avanti, è alla tappa 5 vuol dire che è appena finito il quanto giorno e così via
Ins: quindi cosa dobbiamo guardare per capire bene in che giorno siamo?
Leon: il cartellino della tappa in cui si trova il figlio del re. Così sono sicuro di non sbagliare
Ins: bene
Leon: ora il sesto giorno il figlio del re va alla tappa 6 e il messaggero va alla tappa 3
Gabriel: il settimo giorno il principe fa altri 50 km in avanti e va alla tappa 7, invece il cavaliere fa 100 km arrivando alla tappa 5
Leon: l’ottavo giorno il principe va all’ottava tappa, mentre il messaggero arriva alla tappa 7. Così ora mancano solo più 50 km e poi si incontrano
Ins: siamo tutti sicuri che manchino 50km?
Alice M: no perché poi il principe va ancora avanti e così il messaggero deve fare altri 100km
Giulia: loro si incontrano al nono giorno. La mattina della nona giornata, il figlio del re va alla nona tappa facendo 50km e il messaggero ne fa 100km e arriva anche lui alla tappa 9
Leon: poi però il figlio del re riceve le gemme ma ora vuole la mappa, quindi il messaggero deve tornare indietro.
Davide: può continuare all’infinito
Ins: perché?
Davide: perché ogni volta che si incontrano poi il principe rimanda il cavaliere indietro a prendere altre cose. Secondo me è così.
Ins: ok, con la scenetta siamo riusciti a capire molto bene che il principe va sempre avanti di 50km e guardando il numero della tappa in cui si trova riusciamo anche a capire il girono appena concluso dalla loro partenza. Il messaggero quando è da solo fa 100km, ogni tanto va in avanti e ogni tanto indietro. Infine abbiamo sperimentato concretamente che i due personaggi si incontrano la prima volta il terzo giorno e la seconda volta dopo nove giorni dalla partenza. Come ha detto Davide la storia potrebbe continuare all’infinito, quindi non ci bastano i banchi-tappe, vediamo come avete ragionato ieri nei gruppi.
GRUPPO 1
Davide: noi abbiamo fatto una mappa del figlio del re che ti spiegava che lui va avanti di 50km e l’altra sul messaggero che ne fa 100
Ins: ok però nella vostra mappa non è chiarissima questa cosa. Guardate un po’ cosa avete scritto?
Davide: il terzo giorno ci siamo confusi e gli abbiamo fatto fare 150km in un giorno
Ins: la vostra strategia poteva funzionare ma dovevate stare molto attenti nella rappresentazione. Cosa sarebbe G0?
Davide: è il giorno 0 che indica la partenza, il castello. Poi abbiamo fatto delle frecce avanti e indietro perché abbiamo capito che il messaggero a volte va indietro. Forse per non confonderci al posto di mettere giorno 0, 1, 2, 3 ecc potevamo mettere tappa 0 il castello e poi tappa 1, 2, 3 ecc… come abbiamo fatto nella scenetta prima. Perché così abbiamo confuso i giorni con le tappe
Ins: ok, poi nella vostra mappa quanti chilometri ci sono tra una tappa e l’altra?
Leo C: nella mappa del principe 50km ogni tappa e in quella del messaggero non abbiamo fatto bene, una volta abbiamo messo 50km, poi 150km ma invece tra una tappa e l’altra ci sono sempre 50km anche nella mappa del percorso del messaggero perché sono sempre le stesse tappe
Davide: noi abbiamo sbagliato a contare i km fatti dal messaggero e poi abbiamo sbagliato a contare i giorni
Ins: ok, vi siete accorti di ciò che non andava bene nella vostra strategia. Fare la scenetta sicuramente vi ha aiutato a capire meglio
GRUPPO 3
Alice: noi all’inizio abbiamo provato a fare con delle frecce ma poi non capivamo più nulla, così poi dopo abbiamo capito che sarebbe stato come fare un gioco dell’oca. Abbiamo disegnato il castello che era il nostro start e poi le diverse tappe erano come le caselle del gioco dell’oca
Gabriel: poi abbiamo preso due gomme per fare il figlio del re e del messaggero
(hanno rappresentato il castello e le diverse tappe alla lavagna e poi hanno preso le due gomme per fare i due personaggi, hanno usato la stessa strategia utilizzata il giorno prima e usato la loro tecnica, in questo modo siamo arrivati a capire che il terzo incontro sarebbe avvenuto dopo 27 giorni) Video della strategia risolutiva adottata dal gruppo https://drive.google.com/file/d/1yvaUq62OnKRSO_bl2jO4rgCUxtAqn498/view?usp=sharing
Gabriel: i due personaggi li spostiamo insieme io faccio il cavaliere e Giulia il figlio del re
Alice D: si perché si spostano contemporaneamente, alcune volte nella stessa direzione, altre volte in due direzioni opposte, quando il messaggero va verso il castello.
Ins: ok , spostando contemporaneamente i due personaggi abbiamo capito che il primo incontro avviene…
Giulia: dopo 3 gironi dalla partenza
Leo I: poi il secondo incontro dopo 9 giorni dalla partenza
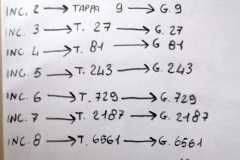
Gabriel: e ora abbiamo visto che il terzo giorno avviene dopo 27 giorni dalla partenza, l’abbiamo capito spostando i personaggi
Ins: dopo che il messaggero porta la mappa al principe al 27° giorno dalla loro partenza, cosa succederà?
Alice D: che sicuramente il principe lo rimanda indietro a prendere delle cose
Ins: chissà dopo quanti giorni si incontreranno di nuovo per la quarta volta
Enea: dopo molti più giorni si incontreranno
Ins: cercheremo anche di capire dopo quanti giorni si incontrano la 4° la 5° la 6° volta ecc, ora però cerchiamo di sentire i ragionamenti fatti da tutti i gruppi. Vedete come i primi due gruppi che hanno esposto hanno utilizzato due modi diversi per cercare di capire meglio gli spostamenti dei due protagonisti. Sentiamo anche gli altri
GRUPPO 4
Filippo: noi abbiamo fatto un po’ come il gruppo 3
Enea: si però noi non abbiamo fatto un unico percorso ma ne abbiamo fatti due e poi abbiamo messo delle frecce
Rebecca: le frecce indicavano i personaggi che andavano avanti e indietro
Lulù: era la direzione
Ins: guardando la vostra rappresentazione di cosa vi accorgete ora che abbiamo fatto la scenetta?
Enea: potremmo mettere tutte le tappe più vicine e metterle alla stessa distanza l’una dall’altra perché sono sempre 50km, potevamo fare ogni 2 centimetri fare una tappa
Ins: ora guardiamo le frecce che avete messo, vanno bene?
Filippo: le frecce viola erano del cavaliere e quelle azzurre del principe. Il principe andava sempre avanti
Rebecca: il messaggero andava avanti poi torna indietro, poi di nuovo avanti
Ins: ok ma guardando la vostra mappa non si capisce bene il percorso del messaggero
Enea: si perché ci siamo sbagliati perché le frecce ci confondevano un po’
Ins: quindi cosa avete fatto
Rebecca: poi anche noi abbiamo usato le gommine con l’altro gruppo e abbiamo capito meglio. Poi qui abbiamo scritto che il terzo incontro è dopo 28 giorni ma perché ci siamo sbagliati perché le tappe poi erano troppo attaccate
GRUPPO 2
Lulù: noi abbiamo usato la tabella per capire cosa succedeva. Una tabella era per il figlio del re e l’altra per il messaggero.
Ins: cosa avete inserito in queste tabelle?
Lulù: da una parte abbiamo messo i giorni, tipo giorno 1 2 3 4 5….. e dall’altra parte i chilometri dove si trovavano.
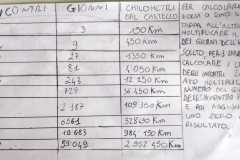
Edo: ad esempio il giorno 1 il principe si trova al 50° km alla tappa 2 si trova al chilometro 100 e così via. Per fare i km del figlio del re perché erano sempre 50 km in più.
Ins: le difficoltà emergono quando bisognava completare la tabella del messaggero.
Davide: e si perché per il principe bastava fare sempre +50 invece per il messaggero bisognava sommare il primo giorno 50 e poi dopo il primo giorno sommare sempre 100
Ins: Siete d’accordo con Davide?
Leo C: a volte bisognava anche sottrarre.
Rebecca: perché a volte il messaggero torna indietro, non va sempre avanti.
Alla lavagna abbiamo corretto la tabella del messaggero e poi confrontata con la tabella del principe.
| FIGLIO DEL RE | MESSAGGERO |
| GIORNO | KM IN CUI SI TROVA | GIORNO | KM IN CUI SI TROVA |
| 1 | 50 | 1 | 50 |
| 2 | 100 | 2 | 50 |
| 3 | 150 | 3 | 150 |
| 4 | 200 | 4 | 50 |
| 5 | 250 | 5 | 50 |
| 6 | 300 | 6 | 150 |
| 7 | 350 | 7 | 250 |
| 8 | 400 | 8 | 350 |
| 9 | 450 | 9 | 450 |
Lulù: il secondo giorno il messaggero di trova al 50° km perché va al castello in mezza giornata e poi l’altra mezza giornata va di nuovo alla tapa 1. Ha percorso 100 ma si trova sempre al km 50 perché l’ha fatto 2 volte
Filippo: il terzo giorno poi si incontrano
Ins: da cosa lo capiamo che si incontrano il terzo giorno
Martino: perché guardando la tabella si vede che si trovano tutti e due al 150° km. Poi il 4° giorno si trova al 150° km e torna verso il castello, quindi bisogna fare -100 che fa 50. Si trova al 50° km
(siamo ancora andati avanti con questo ragionamento fino a capire che si incontrano il nono giorno al 450° km)
Ins: quindi la tabella costruita da questo gruppo cosa segna? I chilometri fatti ogni giorno?
Lulù: no, dice dove si trovano
Ins: esatto, non bisogna confondersi non sono i km fatti ogni giorno ma il chilometro in cui si trovano
Leo C: in questo metodo era più complicato perché a volte bisognava fare -100 e altre volte +100 per il messaggero, invece il principe era facile perché era sempre +50
Enea: anche io la penso come Leo C.
GRUPPO 5
(premetto che non mi è chiaro come abbia ragionato questo gruppo. Loro hanno sommato i chilometri fatti nei vari giorni dal messaggero e dal principe e poi li hanno confrontati, non capisco come siamo arrivati a dire che il secondo incontro avviene il 9° giorno e il terzo al 27° giorno, probabilmente ho posto le domande sbagliate)
Giacomo: noi abbiamo calcolato che sono partiti insieme e entrambi hanno percorso 50km. Dopo il principe dice al cavaliere di tornare indietro. A questo punto lui percorre 100km e arriva al castello, mentre il principe, intanto è avanzato di 50 km. Noi ovviamente tutto questo lo abbiamo sommato. Il principe in 3 giorni fa 150 km
Enrico: e il messaggero ne fa 250, quasi il doppio
Ins: togliendo i chilometri del primo giorno il cavaliere fa sempre il doppio dei chilometri rispetto al principe perché deve tornare indietro. Ok ma sommare tutti i chilometri dei due personaggi, dove vi ha portato?
Giacomo: ci ha portato a dire ad esempio che alla quarta tappa uno ha fatto 200km e il messaggero 350 in totale
Ins: ok ma contando i chilometri fatti in totale alla fine di ogni giorno dai due personaggi, come avete fatto a capire che si incontravano proprio il 3° il 9° e il 27° giorno e non ad esempio il 2° il 7° e il 20°?
Giacomo: noi abbiamo sommato i km che facevano i due personaggi, quando il cavaliere raggiunge il principe lui per raggiungerlo faceva balzi da due perché andava a 100 km al giorno. Quindi si avvicinava sempre di più al principe
Enrico: forse se lo facciamo con delle pedine si riesce a capire meglio
Ins: si, usando le pedine sarebbe il metodo degli altri gruppi e potrebbe funzionare. Io però non ho capito il vostro ragionamento. Riuscite a spiegarmi meglio?
Giacomo: bè noi abbiamo usato sempre la stessa tecnica, abbiamo sommato i km fatti. Il messaggero fa sempre il doppio del km del principe quindi il calcolo ci sta.
(era la fine dell’ottava ora di lezione e non me la sono sentita di portare avanti il discorso , ero fusa anche io, credo che questo gruppo abbiamo sommato i km fatti dai due personaggi capendo che il messaggero, tolto il primo giorno, fa sempre il doppio dei km del figlio del re, però non mi è chiaro come siano arrivati a capire che si incontrano la seconda volta dopo 9 giorni e la terza dopo 27 giorni)
11 giugno 2021