Paola Spolaor, Classe prima, Spinea (VE)
Dopo aver costruito la macchina che mette insieme e aggiunge è ora di cimentarsi con un’altra macchina per affrontare il significato più intuitivo di “sottrazione”: togliere.


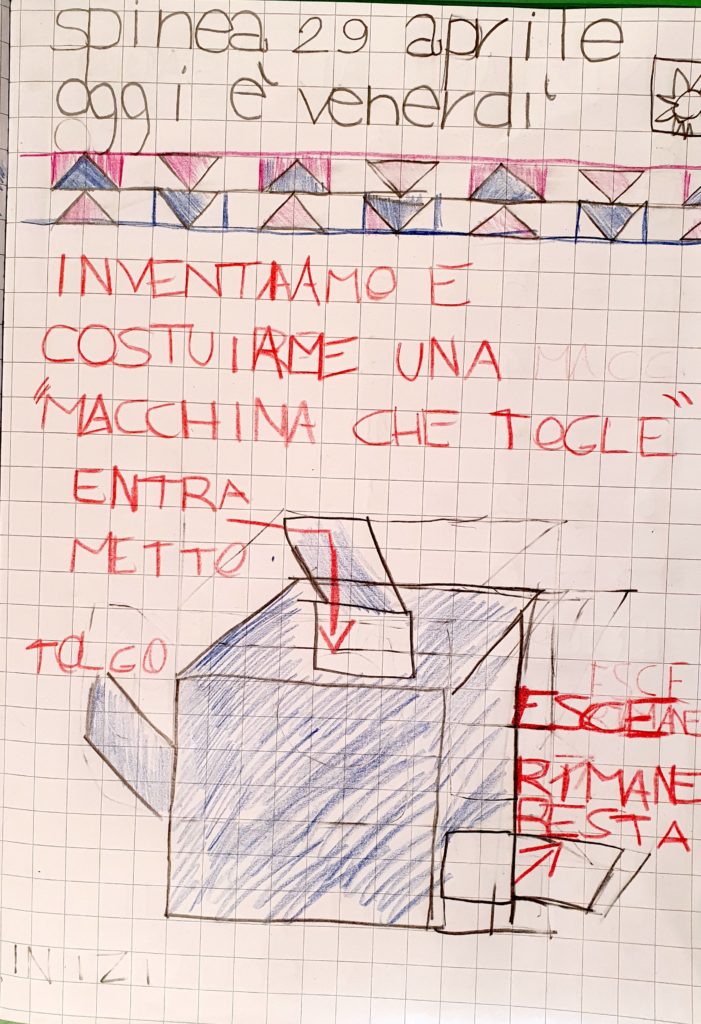



Commento (D.M.): La macchina costruita dai bambini permette di sperimentare solo il significato intuitivo di togliere, azione che viene fatta manualmente dai bambini; ma la sottrazione ha molti altri significati (differenza, quanto manca…) che sono elencati nella classificazione di Moser che metto qui a disposizione:

Commento (D. M.: I problemi inventati da bambini si potrebbero classificare seguendo le indicazioni di Moser per vedere quali significati restano fuori. Inoltre i diversi bambini raccontano delle storie in cui prima del “togliere” c’è un “aggiungere” come si potrebbero tradurre questa situazioni in linguaggio matematico?
Usano anche molto di frequente il “non”: questo è stato indotto o è una loro invenzione (o l’invenzione di qualcuno che ha contaminato gli altri?)? Discorso da approfondire il legame tra la negazione e la sottrazione perchè implica un’idea di inclusione che non è in tutina, va costruita soprattutto perchè nel caso della sottrazione come differenza questa inclusione non c’è più: come rielaborare il significato intuitivo di sottrazione come “togliere” per farla funzionare anche nel caso del confronto?
Commento (D. M.): All’uso della macchina si affianca quello della retta dei numeri introducendo così un altro modello per la sottrazione: come lo intendono i bambini questo andare e venire sulla retta? Si pone ovviamente il problema della sottrazione che non è chiusa per i naturali e i bambini sanno che ci sono numeri sotto lo zero ma non come usarli nelle sottrazioni.
Commento (D. M.): Con l’uso della retta numerica il discorso si fa più complesso: si lavora su una successione che va in due direzioni, andando verso sinistra i numeri diminuiscono (da cui il collegamento con la sottrazione), andando verso destra i numeri aumentano (addizione). C’è da chiedersi, avendo fatto questa duplice esperienza (macchine e retta numerica) quale sia attualmente il significato di struttura additiva che hanno in testa i bambini. Sanno collegare addizione e sottrazione? Le percepiscono come un ‘operazione unica cioè la sottrazione come inversa dell’addizione? dalla discussione parrebbe di sì ma occorre capire quanto questa idea sia patrimonio comune. Quindi non accontentiamoci di poche frasi che vanno nella direzione volute ma facciamo lavorare i bambini in modem specifico su questo aspetto., ad esempio proponendo le terne di numeri che sono collegati da addizione e sottrazione: 2+3=5 da cui 5-3=2 e 5-2=3. Questi fatti devono diventare coscienti per cogliere il nesso tra le due operazioni ed entrare veramente nella matematica.
Le attività suggerite in questa pagina darebbero lo spunto per molte “creazioni” che dovrebbero dare la misura di quanto hanno veramente in testa i bambini; è importante su questi temi avviare molte discussioni per approfondire i diversi approcci e i diversi significati di sottrazione che veicolano. E poi lavorare sui significati mancanti…
Sintesi del lavoro della classe prima
