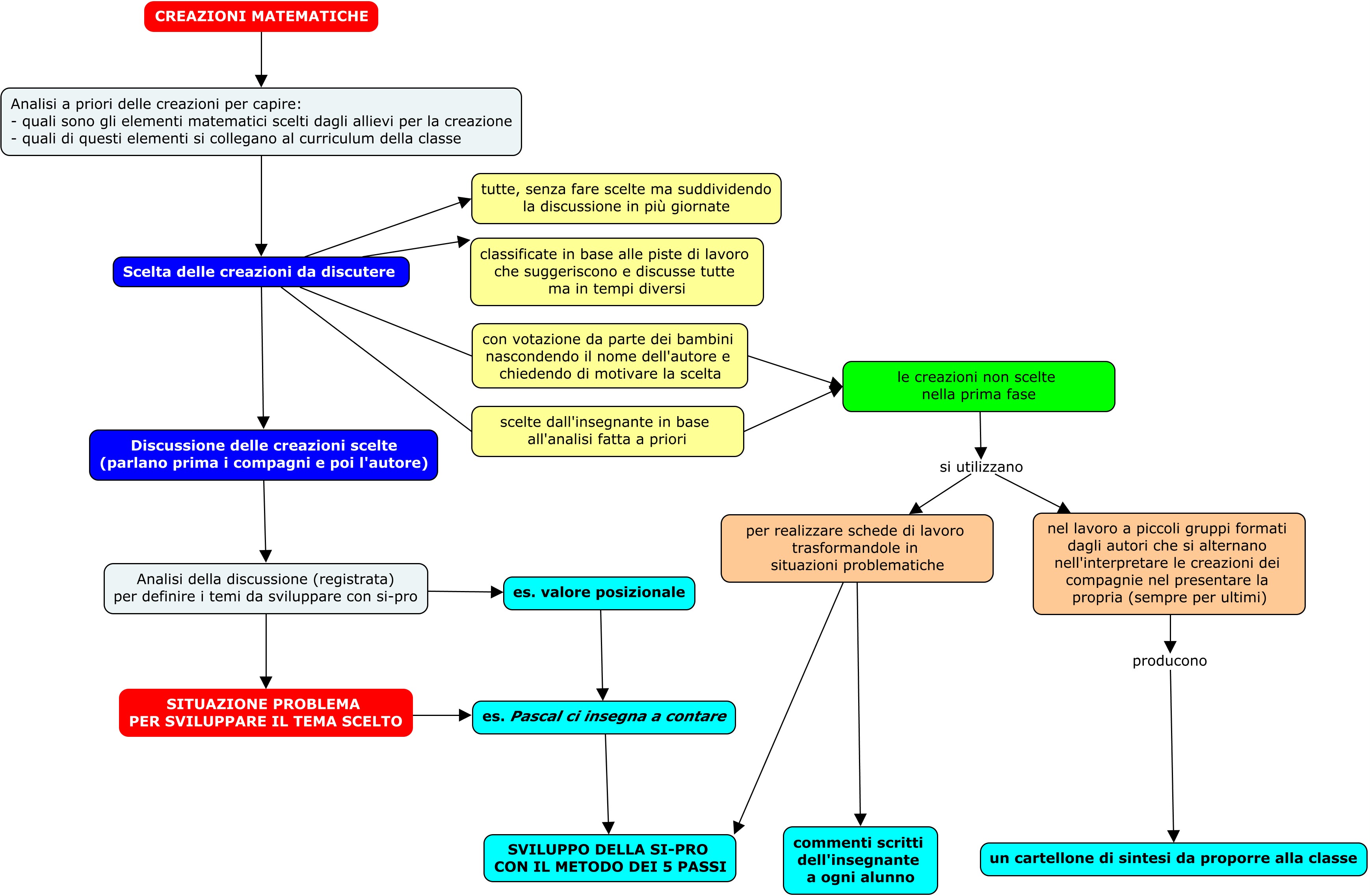
Sono passati alcun i mesi dall’inizio del percorso di ricerca-azione “Fate una creazione matematica!” e gli insegnanti hanno prodotto una quantità notevole di documentazioni sui vari argomenti sviluppati durante gli incontri di formazione più strettamente disciplinari mettendosi alla prova sia sul versante del metodo che su quello dei contenuti.
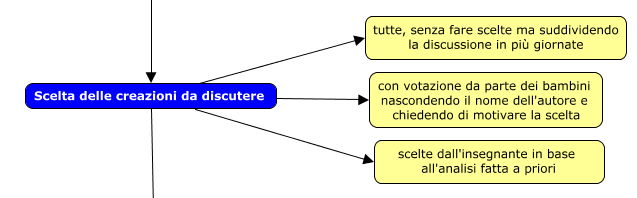
Un problema che stiamo affrontando recentemente è quello della consegna iniziale da dare ai bambini per stimolarli a produrre le loro creazioni soprattutto con i più piccoli che, come succede nella scuola dell’infanzia, non hanno idea di che cosa sia la matematica se non quelli che avendo fratelli più grandi ne hanno sentito parlare in casa.
Questa sfida è stata raccolta da alcuni insegnanti partecipanti al gruppo di ricerca che hanno registrato e trascritto le discussioni fatte con i bambini e le hanno restituite al gruppo. Ho pensato di creare una pagina dedicata a queste discussioni perché può dare dei modelli a chi non ha ancora proposto le creazioni nella sua classe e darci anche l’occasione di riflettere sul nostro percorso.
Trovate le discussioni in questa pagina
Che cosa è una creazione matematica?