Eleonora Deserafini, classe prima, San Germano Chisone (TO)
Lo stimolo delle creazioni matematiche ha dato subito i suoi frutti edi ha suggerito numerose piste di lavoro:














Quali piste di lavoro seguire?
Classifichiamo le creazioni
Ci sono molte tipologie diverse:
LE CIFRE E I NUMERI COME SCRITTURA
Con queste creazioni si può lavorare sulla differenza cifra/numero e sul valore posizionale. Ad esempio nel disegno abbiamo 6 e 5 oppure 8 e 5: che numero rappresentano? e se cambio di posto le cifre cosa cambia? l’1 da solo… il 4 da solo che numero sono? e se di cifre ne metto due che numeri posso fare? Le attività che si possono suggerire sono moltissime (cfr. https://ilpiaceredifarematematica.blogspot.com/2020/04/la-e-pascalina.html)
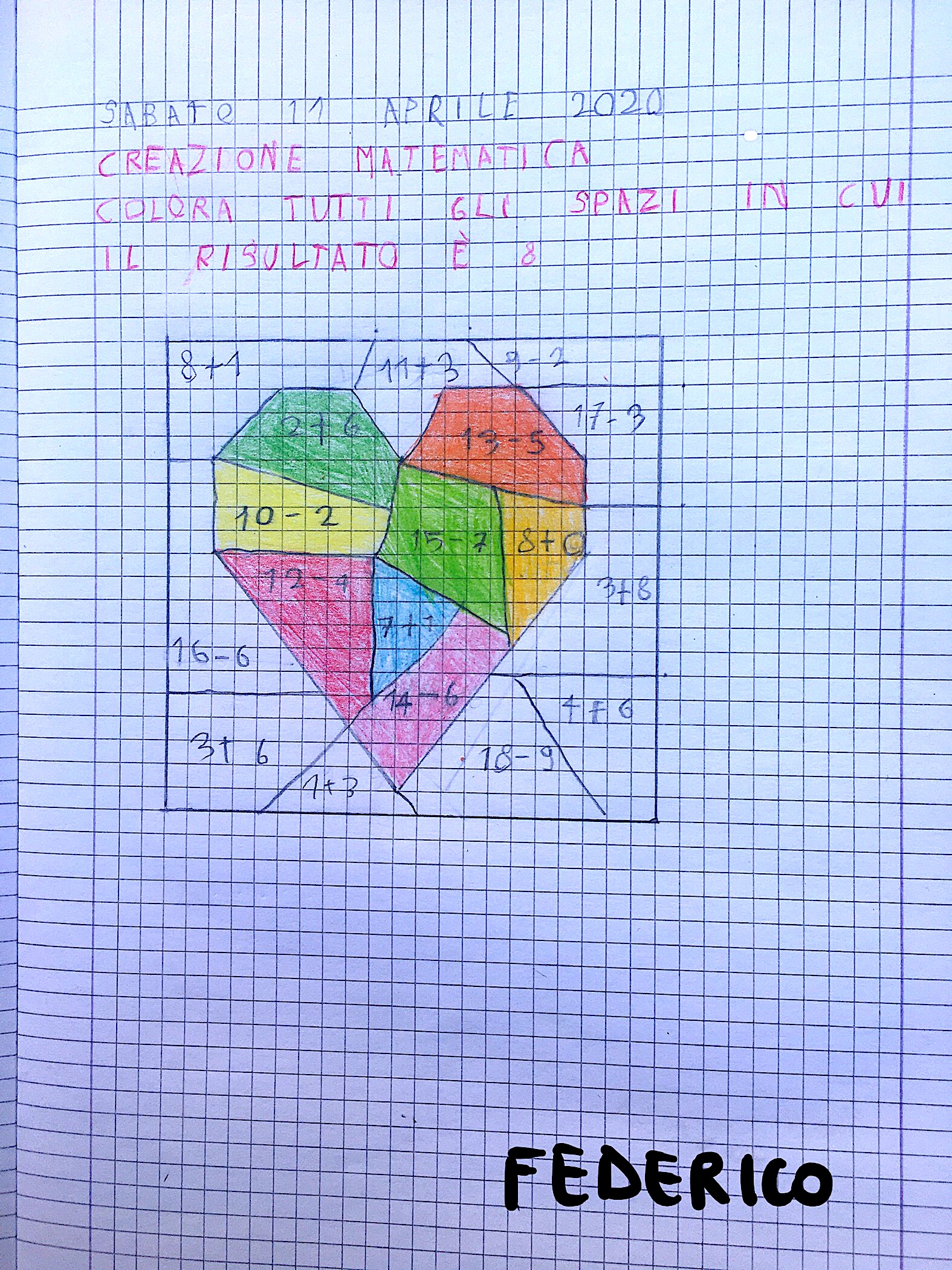
I PROBLEMI ADDITIVI
I bambini attraverso varie attività si impadroniscono della struttura additiva del numero e alcune creazioni suggeriscono questa pista di lavoro che si può ampliare con opportune domande:
- i numeri amici: i numeri che danno 8 ci sono tutti? quanti sono? come si fa per essere sicuri di averli fatti tutti? che ragionamento si deve fare? e con il 7 cosa succederebbe? e con il 5? i bambini devono spiegare per scritto e quindi rendere esplicite le loro strategie
- composizione e scomposizione additive di numeri: ad esempio tutte le scomposizioni da 10 a 20: 10 e 1 10 e 2 10 e 3 10 e 4 ecc. e poi andare anche oltre
La conoscenza dei fatti additivi deve collegarsi con le attività sui problemi per dargli senso. I problemi si costruiscono facilmente da situazioni quotidiane che i bambini vivono a casa. Si possono proporre due tipi di attività:
- tradurre una situazione vissuta in un testo di problema con le sue caratteristiche di genere testuale (situazione, indovinello…), rappresentarla con un disegno che metta in evidenza la strategia risolutiva (disegno spontaneo ed originale); la stessa cosa si ottiene partendo da un’immagine data che suggerisca qualche storia (storie con i numeri);
- partire da un’operazione scritta e chiedere di inventare una storia che si possa rappresentare con l’addizione, la sottrazione… oppure partendo da un’immagine che rappresenti quella scritta, trovare tutte le situazioni additive possibili dirette e inverse (quindi non solo mettere insieme o togliere ma anche trovare quanto manca a…, la differenza tra….): i bambini dovrebbero scoprire il legame che unisce addizione e sottrazione e imparare a trasformare le situazioni in modo da risolvere ora con l’addizione ora con la sottrazione a seconda di come è stata formulata.
IL CONTEGGIO
La creazione del nome con i bottoni suggerisce queste domande:
- quanti bottoni per ogni lettera?
- quanti bottoni in tutto?
- quale lettera ne richiede di più? perché?
- come contarli per essere sicuri di non sbagliare?
Dovrebbe nascere l’idea del raggruppare per…. per rendere più veloce in conteggio. Si possono trovare molte altre situazioni in cui dovendosi confrontare con grandi quantità i bambini devono necessariamente trovare un modo per organizzare il conteggio formando dei gruppi. Inoltre si può lavorare sul confronto allineando opportunamente i bottoni di ogni lettera per creare una corrispondenza biunivoca. Oppure ragionare sulla diversa grandezza dei bottoni.
LE REGOLARITÀ
L’organizzazione della piramide di cioccolatini, degli ometti di pietra, dei legnetti colorati invita a riflettere su vari aspetti, in particolare sui pattern che si possono costruire a partire da qualsiasi materiale ad esempio con i pezzi delle costruzioni; sul sito http://www.visualpatterns.org se ne trovano moltissimi.
Invitiamo quindi i bambini a cercare regolarità e li portiamo così verso l’algebra (la cosiddetta early algebra). In pratica queste creazioni danno l’avvio al discorso delle successioni numeriche, attività molto importante da proporre fin dalla classe prima ma partendo da un pattern visivo il numero è collegato alla percezione spaziale e questo facilità la ricerca delle regolarità. Ciò che dovrebbe essere messo in evidenza è il collegamento tra la posizione di un item e il numero rappresentato nel pattern perché questo induce a successive generalizzazioni.
LA MISURA
Questo tema è aperto dalla creazione con le tavolette di cioccolata e l’uovo di Pasqua: come fare per verificare che sia effettivamente come sta scritto sul foglietto cioè che la cioccolata di un uovo di Pasqua corrisponde a quella di 7 tavolette di cioccolata? In questo caso è stata l’esperienza concreta: sciogliere il cioccolato in tavolette e trasformarlo in uovo di Pasqua con una forma adatta. Un problema importante da affrontare in questa classe è questo: come si fa a dire quanta cioccolata c’è nell’uovo? e nelle tavolette di cioccolata? come si fa a dire che ce n’è la stessa quantità? Questa situazione però ci porta inevitabilmente nel mondo della misura che si può esplorare con attività specifiche, facilmente realizzabili a casa: quanta farina per fare la torta? contiamo le manciate… quanto zucchero nella macedonia? contiamolo a cucchiaiate…. e poi spieghiamo come abbiamo fatto e perchè.
IL SIGNIFICATO DELL’UGUALE
Per esplorare il significato matematico dell’uguale esiste questa bellissima app gratuita per iPhone e iPad https://apps.apple.com/it/app/tiny-human-math-lite/id1244487957 (con > < = costa qualche euro) . La stessa cosa si può simulare facilmente scrivendo su cartoncini le operazioni e chiedendo ai bambini di completarle con i numeri mancanti es. 2 + …….. = 5 + ……, un gioco tipo “bilancia matematica” in cui a destra si pone un’operazione e a sinistra l’altra, i bambini devono scoprire che numeri mancano per ristabilire l’equilibrio.
La discussione delle creazioni
