Sonia Sorgato, classe terza, Milano
Discussione della creazione di Jana
Insegnante: vorrei che disegnaste questa creazione di Jana e poi proviamo a discuterne.
Sveva: mi ricorda un prisma.
Insegnante: hai pensato a un prisma.
Cloe: un prisma con un buco dentro.
Jan Paul: se guardi il triangolo più piccolo mi sembra un corridoio.
Sara: sembra un prisma come ha detto Sveva e anche un corridoio, un prisma con un corridoio, ci sono le pareti che continuano come una caverna fino a che diventa un puntino che si chiude.
Antonio: se io sono qui e cammino vedo questo buco e arrivo fino al buco, è una caverna con un prisma.
Giorgio: mi sembra una piramide a metà, poi ancora la metà, se l’hai tagliata i triangoli sono uguali. Sembra tagliata a metà. Una piramide grande che taglio a metà e mi viene quell’immagine.
Cloe: ah ho capito!
Giorgio: tu la tagli a metà e vedi questo buco che sarebbero le entrate o le stanze.
Davide: sembra la piramide degli Egizi, sembra un corridoio.
Insegnante: ti è venuta in mente la piramide dell’antico Egitto.
Giorgio: anche a me era venuto in mente l’Egitto.
Sveva: vedo dei triangoli sempre più piccoli, ma se tu ti metti un po’ così a guardarlo sembra in 3D.
Insegnante: hai notato che ci sono dei triangoli.
Sabiha: sono dei triangoli.
Malik: ci sono dei triangoli grandi e piccoli.
Gaia: in che modo è tagliata questa piramide?
Insegnante: bisogna chiedere a Giorgio.
Cloe: sembra una grotta triangolare tutta tagliata, oppure tanti triangoli messi in fila dal più grande al più piccolo.
Stefy: mi sembra una piramide tagliata.
Insegnante: io non ho capito bene perché Sabiha, Sveva e Malik hanno parlato di triangoli sempre più grandi invece Giorgio a un certo punto del suo discorso ha detto che questi triangoli sono uguali.
Giorgio: ho capito cosa intendevi! Sono uguali ma lontani!
Insegnante: sono uguali ma lontani. Cerchiamo di capire bene questa cosa.
Davide: ma non sono molto uguali, forse se li facciamo sui fogli a quadretti sono uguali, questi non sono fogli a quadretti quindi sono venuti un po’ storti.
Insegnante: dopo proviamo anche a disegnarli su un foglio a quadretti.
Gaia: sembra che cresca.
Omar: per me sono uguali ma cambia solo la grandezza.
Sveva: l’ultimo è la piramide più lontana, quella grande è la più vicina.
Antonio: ha fatto 3×7, Jana ha osservato bene il disegno e ha fatto 3 punte per 7.
Alessandro: ha fatto uno spicchio di piramide e l’ha tagliata a metà
Jan Paul: è come un arcobaleno ma geometrico con i triangoli.
Insegnante: Omar, ripeti quello che hai detto…
Omar: i triangoli sono uguali ma cambia solo la grandezza.
Cloe: quello che ha detto Omar è vero ma se io guardo una cosa da lontano è più piccola, per esempio se io prendo il mio astuccio da lontano è molto più piccolo. Se io vado vicino a un oggetto più piccolo può sembrare più grande di un altro che è più grande ma più lontano.
Insegnante: abbiamo visto ancora questa cosa che ha raccontato Cloe.
Sara: l’abbiamo visto con il drone, quando saliva vedevamo le cose piccole, eravamo piccoli, quando si avvicinava erano molto più grandi.
Ale: è come quello che ha detto Sara, quando il drone è salito la chioma degli alberi impediva di vedere il tronco.
Sveva: l’abbiamo visto anche un’altra volta, quando abbiamo studiato le ombre con le forme mettendole davanti alla luce e poi abbiamo osservato ancora con la luce del sole in giardino.
Gaia: quando il drone andava su noi eravamo un puntino.
Sveva: quando abbiamo fatto il disegno con il drone, noi eravamo dei puntini e poi c’era tutto il parco visto dall’alto.
Ale: abbiamo fatto anche tutto un disegno per fare una mappa. È molto diversa la prospettiva della visione.
Insegnante: parla l’autrice.
Jana: mi è venuta questa idea: il per e il diviso e altre cose. Prima di fare 3×7 ho fatto i triangoli che hanno 3 punti come ha detto Antonio e poi mi sono venute tante idee 3+3+3+… per fare 21. Quando ho fatto i triangoli mi è venuta un’idea come ha detto Giorgio, sono uguali ma più piccoli.
Poi ho fatto 3×7. 3 sono i lati di un triangolo.
Antonio: io ho pensato agli angoli e ai punti visto che il triangolo ne ha 3. Il triangolo deve avere sempre la stessa forma. Quelli dentro sono sempre triangoli. Ha contato quanti angoli c’erano.
Jana: ho fatto prima il triangolo piccolo e poi quelli grandi, ho visto quanti ce ne possono stare.
Insegnante: quanti ce ne possono stare?
Jana: 7
Gaia: 10
Antonio: infiniti.
Sveva: in base alla grandezza del foglio.
Insegnante: ma se io parto dal grande quanti ne posso fare di più piccoli rispetto a quello che ho disegnato? Anche se magari non lo posso fare ma nella nostra immaginazione…
Jana: ognuno rimane della sua idea.
Antonio: sono sempre infiniti…
Insegnante: e se avessimo usato i quadrati?
Jana: ci sono anche altri modi.
Il problema dell’angolo
03.02.2021 Dettato di figure geometriche
L’insegnante ha organizzato lo spazio in modo che ci sia un banco coperto da un telo bianco. A turno, dopo averla scelta, consegna a un bambino/a una figura geometrica in gomma eva. Il bambino/a si nasconde sotto al banco coperto e deve cercare di far indovinare la figura ai compagni che hanno il compito di disegnarla, ciascuno sul proprio foglio.


GAIA E IL RETTANGOLO
Insegnante: Descrivi com’è fatta questa figura senza dire come si chiama.
Gaia: ma io non so come si chiama
Insegnante: Meglio!
Gaia: Ha due righe lunghe, ha una riga corta e anche un’altra riga corta.
(I compagni iniziano a intervenire)
Insegnante: Hai finito la descrizione o puoi dire anche un’altra cosa?
Gaia: Ho finito
Insegnante: Possono iniziare le domande poi io ti dico se puoi rispondere
Cloe: Gaia, ma le righe lunghe sono in verticale o in orizzontale?
(Gaia sta in silenzio)
Cloe: Magari sono così o così
Giorgio: Ma cosa dici così o così Cloe che non ti vede neanche
Gaia: In orizzontale
Alessandro: Ma è lungo? Cioè è una forma lunga?
Gaia: Un po’ lungo
Cloe: La possiamo disegnare?
Insegnante: Sì, se avete capito la potete disegnare con matita e righello, è un disegno geometrico!
Sara: Quante righe ha questa forma?
Gaia: Ne ha quattro
(Alcuni bambini esclamano: “Ecco!” “Lo sapevo!”)
Insegnante: Scusate, come si chiamano le righe, il termine un po’ più specifico?
Jan Paul: Segmenti!
Insegnante: I segmenti però possono anche essere da soli. Come si chiamano quelli delle figure?
Arianna: I segmenti retti
Insegnante: Retti nel senso che sono dritti? C’è un altro termine, ve lo dico io, si chiamano lati.
Molti manifestano i fatto che hanno capito di che figura si tratta, Gaia può uscire e chiama Ginevra.
Ginevra: E’ un rettangolo!
Insegnante: E’ un rettangolo Gaia?
Gaia: No
Giorgio: Ma se non sa il nome? Non è un quadrato, un quadrato non ha due linee lunghe e due linee corte.
Sveva: Ma ha tre lati?
Gaia: No, ne ha quattro
Giorgio: E allora io cancello!
Insegnante: Aspettate a cancellare!
Sveva: Ma è tipo un parallelelpipedo?
Insegnante: Il parallellepipedo però è un solido, tu forse intendi un parallelogramma?
La classe decide che è un rettangolo!
Insegnante: Perchè pensate che sia un rettangolo?
Cloe: Perchè ha detto che due linee corte e due linee lunghe e ha quattro lati. Cos’è? Il quadrato ha le linee uguali.
Insegnante: (prende il disegno di Marco e lo mostra alla classe) però potrebbe essere questo. Anche questa figura ha due lati lunghi e due corti.


Giorgio: E’ un rettangolo!
Insegnante: Questo non è un rettangolo. Gaia ha fatto questa descrizione: ci sono due lati lunghi e due corti, questo corrisponde a questa descrizione.
Giorgio: Anche il rettangolo corrisponde alla descrizione.
Insegnante: Quindi che differenza c’è?
Alessandro: Quello di Marco è come se fosse spezzata una parte del rettangolo, una parte di triangolo, mentre quello di Arianna è un rettangolo.
Insegnante: Sentiamo altre ipotesi
Sveva: La differenza tra quello di Arianna e quello di Marco è che quello di Marco ha le linee messe oblique invece quello di Arianna ha le righe dritte.
Insegnante: Dritte che cosa vuol dire? Se lo metto così è dritto? (Prende il foglio di Arianna e lo inclina)
Bambini: Sì.. No…
Insegnante: Cambia forma? Non è più un rettangolo?
Antonio: No!
Insegnante: Cosa vuol dire dritto?
Cloe e Alessandro: Quello è un rettangolo!
Sveva: I lati sono dritti
Insegnante: E’ giusto quello che hai detto Sveva, ma come possiamo dire allora?
Cloe: Guarda, se lo vedi sul foglio qua sono dritte. Anche il foglio è un rettangolo e anche se lo giri così è un rettangolo. Sono due rettangoli.
Insegnante: Sì, ma Sveva ha detto che i lati sono dritti tra loro. Teniamocela in mente perchè è una cosa molto importante. Facciamo vedere la figura!
Giorgio: E’ un rettangolo!! L’abbiamo detto tutti e lei hai detto di no!
Solayman: Allora dobbiamo cancellare?
Insegnante: In matematica non si cancella niente!
Giorgio: ma tu sei una bugiardona!! Quello è un rettangolo!
Insegnante: Ma forse non sapeva che si chiama rettangolo…
Giorgio: Ma che razza di geometria hai!
Insegnante: Gaia, questa figura si chiama rettangolo e l’hai descritta benissimo perchè hai detto che ha due lati lunghi e due corti. Quello che ha disegnato Marco si chiama parallelogramma.
ALESSANDRO E IL ROMBO
Alessandro: Ha due lati uguali … e ha quattro lati.
(Alessandro ha la voce un po’ bassa e i compagni gli chiedono di ripetere)
Alessandro: Ha quattro lati!
Cloe: ha sei lati??
Jan Paul: Ma se ha detto che ha quattro lati!
Alessandro: Ho finito
Antonio: Ma ha due lati lunghi e quattro lati?
Cloe: Ha sei lati quindi?
Alessandro: No, in tutto ha quattro lati
Cloe: Allora perchè hai detto che ha due lati e quattro lati?
Alessandro: No, non ho detto così.
Insegnante: Allora spiegati Alessandro perchè si vede che non è chiaro.
Jan Paul: Ha quattro lati in tutto uguali.
Insegnante: Alessandro, Jan paul dice così, è giusto?
Alessandro: Credo di sì.
Insegnante: Ha quattro lati uguali?
Alcuni bambini consigliano di utilizzare il righello per verificare che siano quattro lati uguali.
Insegnante: No, sbagliatissimo il righello!
Cloe: Ma se ci dici sempre di farlo con il righello!
Insegnante: Il righello per disegnare ma per vedere se una figura ha i lati uguali dovete vedere con gli occhi e il ragionamento.
Gaia: Si possono fare due figure?
Insegnante: Certo! E’ venuta fuori una cosa molto interessate!
(Alessandro chiama Solayman)
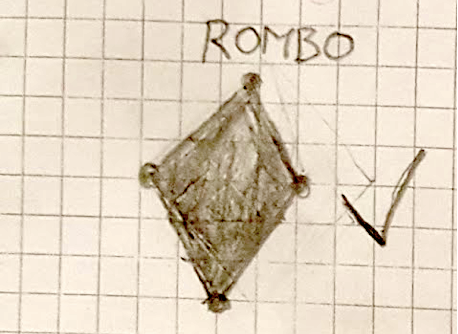
Solayman: E’un rombo
Alessandro: Non so come si chiama quella forma…
I compagni di classe fanno vedere con le dita al compagno che forma ha un rombo, come un aquilone, come due piramidi una sopra e una sotto.
Insegnante: Attenzione però perché Alessandro ha detto che ha tutti i lati uguali.



Alessandro: Sì, è un rombo!
Insegnante: Facciamo attenzione a una cosa. Il rombo ha tutti i lati uguali come che cosa?
Ginevra: Come il cubo!
Insegnante: Il cubo è un solido, noi stiamo parlando di figure.
Cloe: Il quadrato.
Insegnante: Alessandro, Arianna ha seguito quello che hai detto tu: ha quattro lati, due sono uguali. Ha la forma di un aquilone e si chiama deltoide.
Ma la tua figura non è questa. Come possiamo descriverlo in modo da essere sicuri di disegnare questa figura (rombo) e non il deltoide e non il quadrato?
Perchè il quadrato è un rombo perchè ha quattro lati uguali, però è un rombo molto particolare. Che cosa ha di particolare rispetto a questo (rombo)?
Matteo: Basta che dici rombo e si spiega tutto
Insegnante: D’accordo ma se la regola è di non dire il nome?
Jana: (Prende in mano il rombo) Questo è un rombo ma se lo giriamo così non diventa un quadrato.
Insegnante: (Prende in mano il quadrato e lo ruota) Questo se lo metto così che cos’è?
Antonio e altri: Un rombo
Insegnante: No,… anche se è così (quadrato girato in senso tradizionale) è un rombo, ma è un rombo particolare, sia che lo metta così, così, così rimane sempre un rombo particolare, cioè un quadrato.
Insegnante: E’ come se dicessi: io sono una donna, mi chiamo Sonia, sono una donna particolare perchè mi chiamo Sonia.
Jana: Sei sempre una donna se ti giri così, così o così.
Insegnante: Non è che se mi chiamo Sonia non sono più una donna. Sono sempre una donna, come questo è sempre un rombo, però oltre a essere una donna mi chiamo anche Sonia. Oppure posso dire oltre a essere una donna ho i capelli castani. Non è che se ho i capelli castani non sono più una donna.
Cloe: Non è che se ti capovolgi diventi un uomo.
Insegnante: Che differenza c’è tra questo e questo (mostra rombo e quadrato)?
Cloe: Quello è un rombo e quello è un quadrato.
Insegnante: Ok, si chiamano in maniera diversa ma che differenza hanno?
Omar: I lati sono così e l’altro così (mostrando con le mani che i lati diventano obliqui).
Insegnante: Attenzione che tutte e due le figure hanno quattro lati uguali.
Solayman: Questo è più grosso (indicando il quadrato)
Insegnante: Hai ragione!

Insegnante: Che forma è questa?
Malik: Quadrato
Insegnante: Questo è un quadrato. Se faccio così (restringe due vertici verso il centro) i lati rimangono sempre uguali o cambiano?
Omar: Cambiano
Insegnante: Assì, ho cambiato lo stuzzicadenti?
Bambini: Sì, no… no, no.
Insegnante: Allora i lati sono uguali nel rombo e nel quadrato, sono quattro lati uguali.
Cosa cambia allora se faccio così (allarga e restringe gli angoli)?
Giorgio: Diventa più lungo
Solayman: I vertici, l’allargatura, la grandezza, non lo so…
Sveva: Diventa più schiacciato
Insegnante: Quindi cosa cambia?
Jana: Cambia la lunghezza
Insegnante: No, gli stuzzicadenti sono sempre quelli, guarda, ne ho presi quattro uguali (e mostra i 4 stuzzicadenti una accanto all’altro)
Solayman: Cambia che quando è un quadrato è più largo e quando fai così è più stretto.
Insegnante: Quando è più stretto diventa un rombo. Quindi cosa cambia di questa figura? Cosa si modifica? I lati abbiamo detto di no
Alessandro: La prospettiva?
Insegnante: No, la prospettiva no perchè siamo sul piano.
Insegnante: Proviamo a fare un’altra figura perchè dobbiamo capire che cosa cambia.
Cloe: Si trasforma!
MALIK E IL TRIANGOLO
Malik: Ha tre lati.

Anche piegare il telo utilizzato per il gioco diventa un’attività di matematica con vertici e lati.
Seconda attività: rotazioni ad occhi chiusi


Tecnologia: forme e misure



