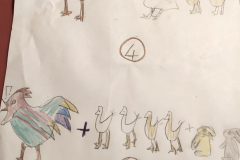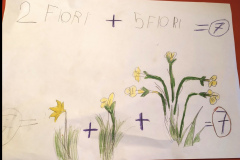Angela Chiappa, classe terza, Piacenza
La discussione delle creazioni
Lavoro di gruppo su una prova del Rally matematico

Gli alunni hanno disegnato le cassette in modo corretto, la media il doppio della piccola e la grande il doppio della media, e hanno aggiunto il numero di arance da mettere in ogni cassetta, mettendo il 48 nel punto sbagliato. Non hanno spiegato come hanno ragionato ma a me hanno raccontato che dopo aver disegnato le cassette, “hanno fatto delle prove”, quindi sono andati per tentativi. Sono partiti mettendo 10 arance nella cassetta piccola.
Se la piccola ne conteneva 10, nella media ce ne dovevano essere 20 e nella grande 40. Così in tutto però sarebbero state 70. Siccome erano poche hanno provato con 11. 11 nella piccola, 22 nella media, 44 nella grande, 77 in tutto. Ancora poche hanno provato con 12. 12 andava bene, hanno scritto il numero sulle cassette anche se il 48 non lo hanno scritto al posto giusto.
Gli alunni non sanno calcolare la divisione quindi risolvono per tentativi ed errori. Questa situazione potrebbe essere il punto di partenza per ragionare sugli algoritmi di divisione. In genere i bambini fanno delle addizioni per trovare il risultato della divisione e da lì poi si riparte per trovare metodi più efficaci e veloci …. senza perdite di senso.
Partendo dalla strategia “naturale” per tentativi ed errori i bambini dovrebbero essere titillati a trovare una strategia che permetta di trovare subito il valore 12 senza fare i tentativi. Si tratta di fare dei ragionamenti a ritroso. Siccome arrivo a 84 facendo due volte il doppio che succede se parto da 84 e faccio il contrario cioè dimezzo? Parto da 84, dimezzo e trovo 48, poi dimezzo ancora una volta e trovo 24, dimezzo ancora e trovo 12. Ho raddoppiato due volte e ora ho dimezzato tre volte perché devo avere tre numeri da sommare (48, 24 e 12) essendo tre le scatole, e infatti sono proprio questi tre numeri che sommati danno 84. Come esce il : 7 da questo ragionamento? Sono rimasta volutamente su un ragionamento solo matematico, senza rappresentazioni. La cassetta da 12 è come una unità di misura e ripercorrendo la sequenza questa volta a partire da 12 posso anche vederla così: 12 + (12+12) + (12+12+12+12)… 7 volte 12… se 12×7=84 allora 84:7=12… Così teniamo insieme moltiplicazione e divisione. Sarei curiosa di vedere altri modi di ragionare perché la rappresentazione con i disegni delle scatolette mi sembra perfin troppo evoluta. Il bambino che l’ha pensata è stato veramente bravo. Ma io mi chiedo: nessuno ha sbagliato? E chi ha sbagliato che tipo di errore ha fatto?
Ora ragioniamo in altri modi… coerenti con la nostra ricerca.
E se invece di 84 la somma fosse stata…. posso mettere qualsiasi numero come risultato o ce ne sono solo alcuni che vanno bene? Perché? Da quanto ho scritto prima le 7 scatolette possono essere riempite da qualsiasi numero: la situazione si può quindi algebrizzare sostituendo a 12 una lettera (o una scatoletta): a + 2a + 4a = 84, se rendo variabile anche 84 avrò che a + 2a + 4a = x cioè 7a=x da cui posso dedurre che x deve essere per forza un multiplo di 7 altrimenti non trovo dei numeri interi. E le arance devono essere intere… il gioco può ovviamente continuare… E se raddoppiassi ancora una volta? a + 2a + 4a + 8a = x … 15a = x … i multipli di 15… E se raddoppio solo una volta? …. I multipli di 3 …. E se la prima volta raddoppio e la seconda triplico? Questa è la ricerca matematica che penso potrebbero fare i bambini.
Ricordiamoci che l’algebra nasce quando si comincia a ragionare su delle relazioni e si crea un “discorso” in cui al posto di valori numerici fissi si introducono delle variabili e delle costanti. Si potrebbe allora riformulare il problema iniziale in questo modo: “Ho una certa quantità di arance con cui riempire tre cassette con questa regola: nella prima cassetta metto un certo numero di arance, nella seconda ne metto il doppio e nella terza il doppio della seconda. In questo modo non avanzo nessuna arancia. Trova almeno due quantità di arance con cui sia possibile fare questo gioco.”
Sarebbe interessante inviare lo stesso problema a ragazzi della scuola media… e vedere se sanno rispondere… e come fanno.