Silvana Testa, classe quarta, San Matteo delle Chiaviche (MN)
Condivido le creazioni fatte da alcuni bambini della classe 4° sul tema delle frazioni che fanno capire quale sia la loro idea di “frazione” attualmente e fanno anche intravedere possibili piste di lavoro.
CREAZIONE MATEMATICA DI ALICE G.
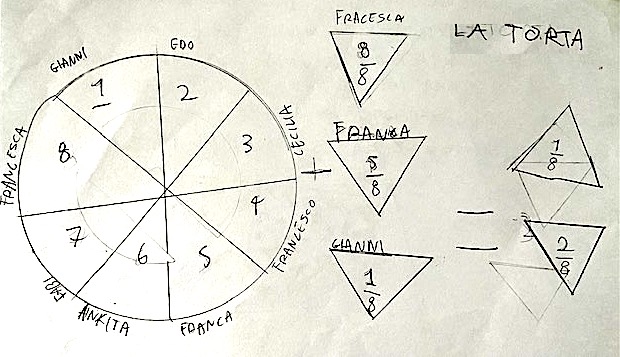
HO FATTO UNA TORTA E HO ASSEGNATO UN PEZZO AD OGNUNO. SE FRANCESCA, FRANCA E GIANNI MANGIANO IL LORO PEZZO POI NE RESTANO 5. QUINDI È UNA CREAZIONE MATEMATICA SULLE FRAZIONI PERCHÉ MANGIANO POCA TORTA E NE RESTA DI PIÙ.
CREAZIONE MATEMATICA DI ALICE P.
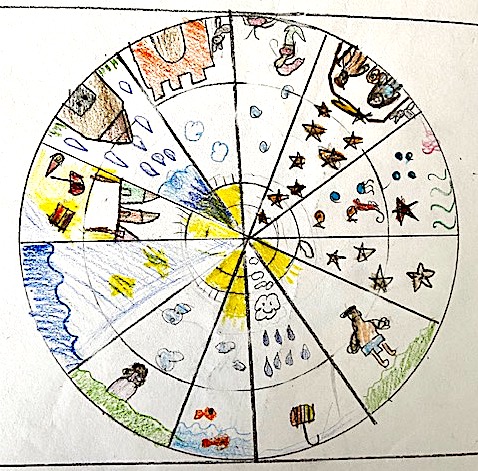
HO DIVISO UN DISCO IN TANTE FETTE UGUALI E OGNI FETTA RAPPRESENTA UNA FIABA DIVERSA.
CREAZIONE MATEMATICA DI ANKITA
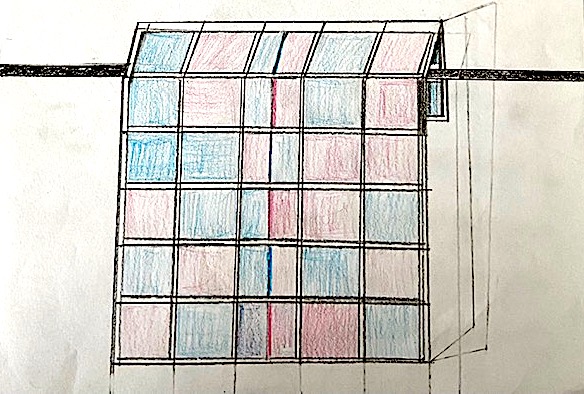
SECONDO ME È UNA CREAZIONE MATEMATICA SULLE FRAZIONI PERCHÉ HO DISEGNATO UN ASCIUGAMANO E L’HO DIVISO IN PARTI UGUALI E L’HO FATTO A FORMA DI QUADRATO.
CREAZIONE DI EDOARDO
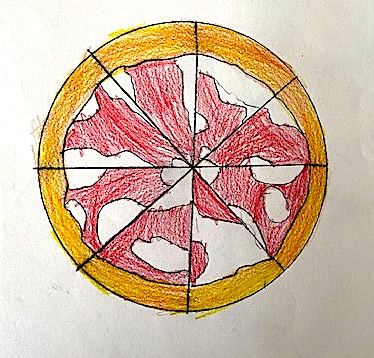
HO DIVISO UNA PIZZA IN 8 PARTI UGUALI
CREAZIONE MATEMATICA DI GABRIELE

SECONDO ME È UNA CREAZIONE MATEMATICA SULLE FRAZIONI PERCHÉ L’HO DIVISA IN PARTI UGUALI.
CREAZIONE MATEMATICA DI GIOVANNI

QUESTO È UN TIRO A BERSAGLIO CON LE FRECCETTE E SECONDO ME È UNA CREAZIONE CHE C’ENTRA CON LE FRAZIONI PERCHÉ GLI SPAZI BIANCHI SONO 9 MENTRE 5 SONO LE PARTI COLORATE DI ROSSO 9/9 E 5/5 QUINDI È UNA FRAZIONE.
La corrispondenza con una classe quinta
Lettera ai bambini della classe 5° di Francesca Liaci. Abbiamo scritto così:
“Noi sappiamo che frazionare significa dividere in parti uguali, ma vorremmo saperne di più!
Le nostre curiosità sono:
– Perché sono state create le frazioni? A cosa ci servono nella vita?
– Come si fa a frazionare qualcosa che non è divisibile in parti uguali?
– Si può frazionare l’infinito?
– Come si fa a frazionare della farina o del liquido?
– Le frazioni a cosa ci servono se abbiamo le divisioni?
– Si può frazionare un numero con la virgola?
– Ci mandate una creazione matematica?
Scusate per tutte queste domande ma la nostra curiosità è davvero tanta.
Vi manderemo presto anche delle creazioni matematiche sulle frazioni che abbiamo fatto!”
La lettera originale:
Discussione delle creazioni di Alice e Edoardo
Nella discussione emerge il conflitto tra due modi di intendere la scrittura 1/8.. 2/8 ecc. Per Alice le frazioni 1/8 2/8 3/8 ecc. servono a “numerare” gli 8 pezzi uguali di cui è composta una torta … per altri invece tutti i pezzi sono 1/8. Come risolverlo?
La risposta dei corrispondenti
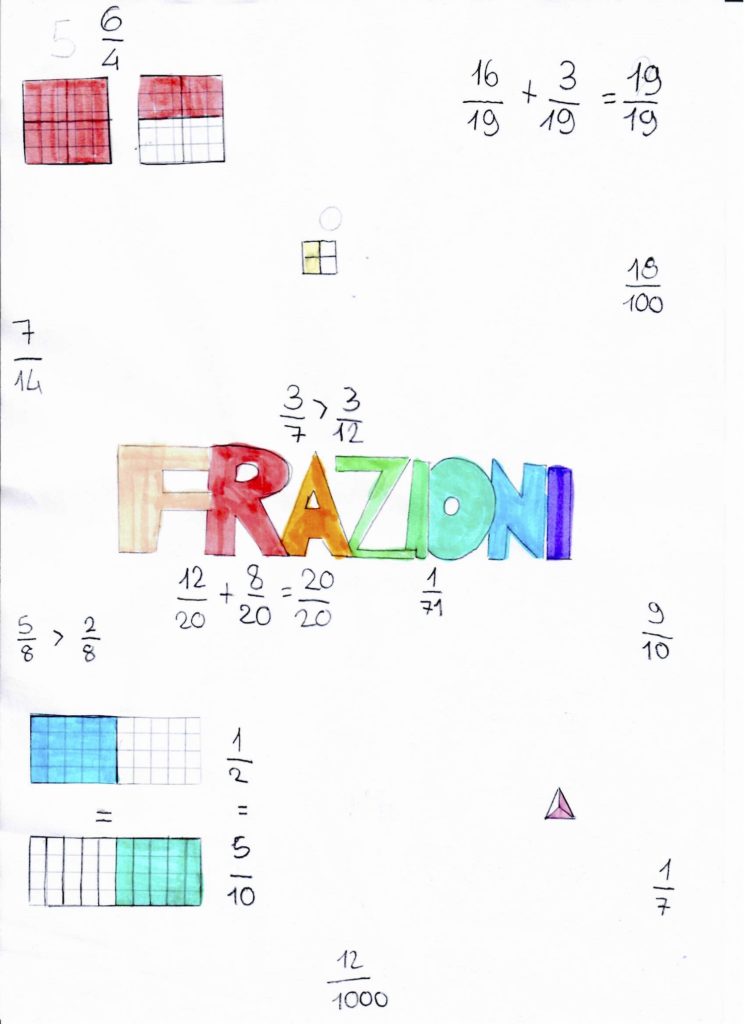


Come è proseguito il lavoro
Commento D.M.: Il lavoro del gruppo 4 si può considerare una creazione perchè ha messo in gioco tante idee diverse che andrebbero approfondite ad esempio il discorso sulla simmetria. ma anche quello dell’equiestensione che, facendo fare le frazioni di grandezze continue, va preso sempre seriamente in considerazione, cioè da intuizione deve diventare conoscenza. Di fatto i bambini ragionano sul conteggio dei quadretti quindi su un un’uguaglianza numerica. Il problema del RMT penso che avesse questo come obiettivo: far ragionare sull’equiestensione e Ankita lo cita a proposito. Che cosa avete fatto sulle aree? E sulle isometrie? Più che sul conteggio dei quadretti dove c’è la simmetria dovrebbe essere questa a garantire l’uguaglianza per sovrapposizione. E poi c’è il discorso dei mezzi quadretti che mi pare risolvano bene contatto mezzo+mezzo=1. Questo andrebbe reso esplicito chiedendo di spiegare come hanno fatto a contare 16 quadretti dove i quadretti erano solo a metà. Non tutti potrebbero aver capito, soprattutto i più fragili.
Sarebbe interessante a questo punto riprendere le creazioni per cercare di capire se gli ostacoli evidenziati allora siano stati veramente superati: avrebbe senso proporre di correggere quelle che contengono ambiguità, idee discutibili…?
