Antonella Varesi, classe terza, Agazzano (PC)




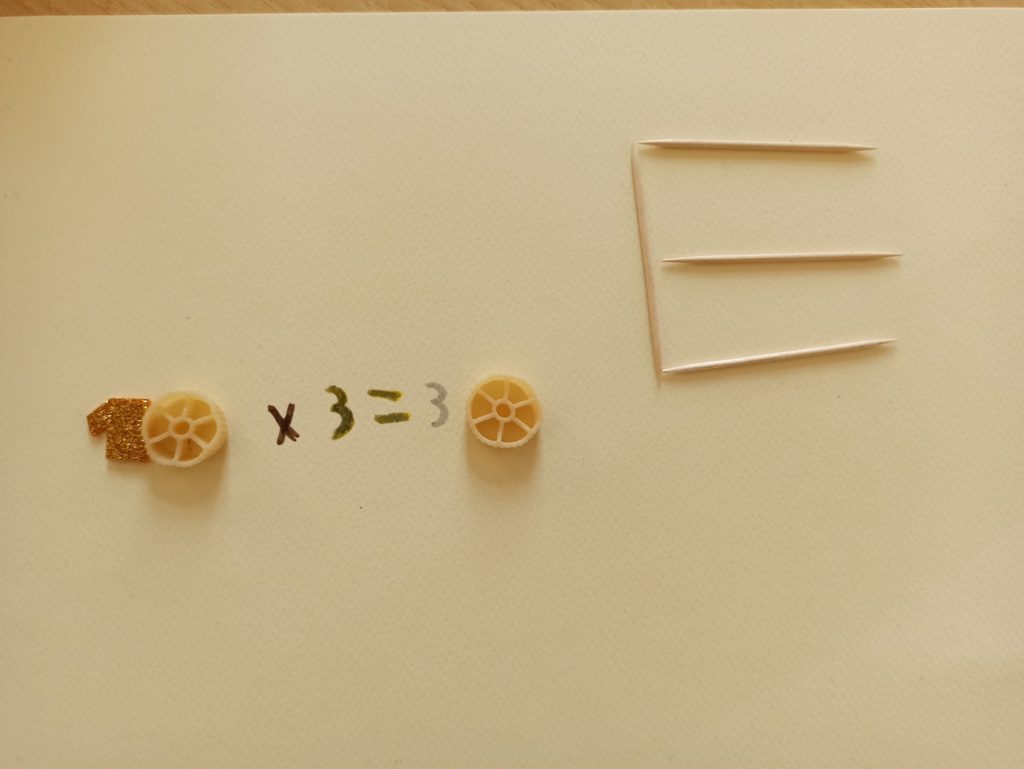











Un Padlet per commentare a distanza le creazioni dei compagni
Le attività precedenti
La scelta della creazione di Ahmed è stata fatta per sviluppare il discorso sui numeri decimali e sulle frazioni. Le attività svolte precedentemente sono documentate nei file pdf e nelle immagini seguenti:
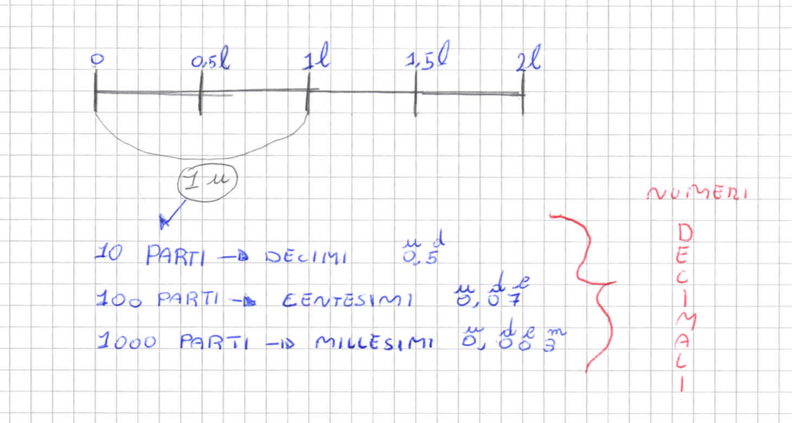




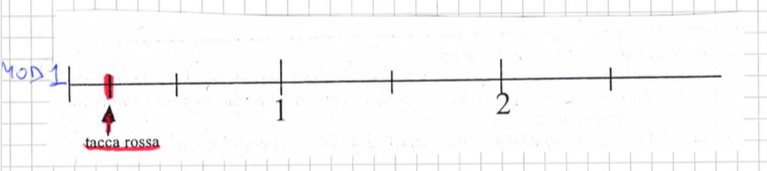
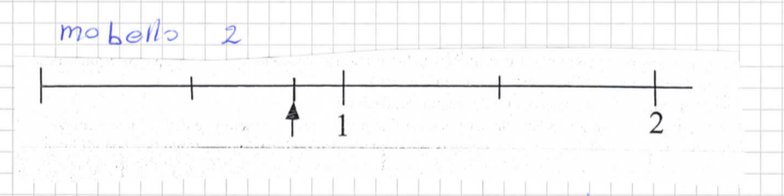

PROBLEMA SULLE FRAZIONI: Le tavolette di cioccolata
4 BAMBINI DEVONO DIVIDERSI IN PARTI UGUALI 3 CIOCCOLATE. COME POSSONO FARE? INVENTA UNA STRATEGIA E RAPPRESENTALA.
PROBLEMI DI PROPORZIONALITÀ: Le ricette
22 marzo 2021
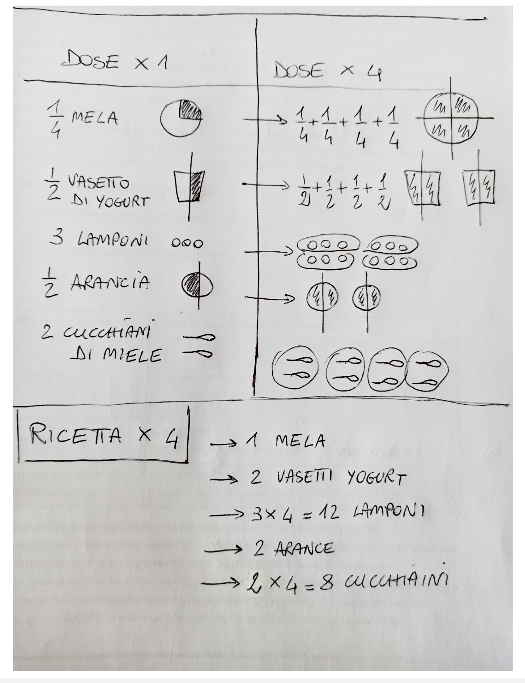
RICETTA PER LA MACEDONIA DI FRUTTA E YOGURT DOSE PER 1 PERSONA
– MEZZO VASETTO DI YOGURT
– UN QUARTO DI MELA
– 3 LAMPONI
– MEZZA ARANCIA
– 2 CUCCHIAINI DI MIELE
ABBIAMO UN PROBLEMA DA RISOLVERE: LE DOSI DELLA RICETTA SONO PER 1 PERSONA MA DOBBIAMO PROCURARE GLI INGREDIENTI PER 4 PERSONE.
24 marzo 2021
RICETTA PER FARE LA PASTA DI SALE PER REALIZZARE 2 LAVORETTI.
– 2 BICCHIERINI DI SALE FINO POLVERIZZATO
– 4 BICCHIERINI DI FARINA
– 2 BICCHIERINI DI ACQUA TIEPIDA
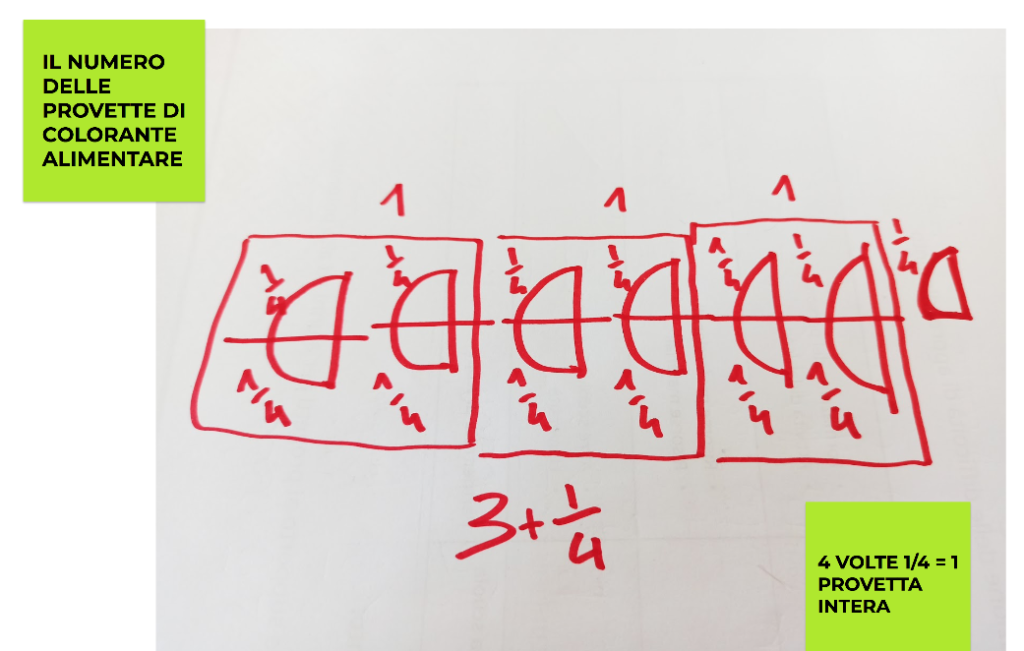
– MEZZA PROVETTA DI COLORANTE ALIMENTARE
ABBIAMO UN PROBLEMA DA RISOLVERE NOI VOGLIAMO REALIZZARE 13 FORMINE.
La macedonia e la pasta al sale (protocolli su jamboard in DaD)



LA CREAZIONE DI AHMED

DISCUSSIONE
LA SITUAZIONE PROBLEMA: Dove collochiamo 3,25 sulla retta numerica?
CONSEGNA: OGGI FATE UNA CREAZIONE MATEMATICA A TEMA ISPIRANDOVI ALLA CREAZIONE DI AHMED: CREATE DUE RETTE NUMERICHE IN CUI COLLOCARE IL NUMERO 3,25.
- USATE I MATERIALI E GLI STRUMENTI CHE VI SEMBRANO PIU’ ADATTI.
- SPIEGATE PER SCRITTO COME AVETE FATTO A COSTRUIRLA E PERCHE’ AVETE COLLOCATO QUEL NUMERO IN QUELLA POSIZIONE.
Materiali: spago, filo di lana, bottoni, stuzzicadenti corti e lunghi, tappi, colla, patafix, nastro adesivo, pennarelli, due strisce di carta bianca per ogni gruppo di lunghezze diverse, righelli, cotton fioc
GRUPPO 1
Ha iniziato disegnando nella striscia di carta più corta una pista doppia ed attaccando un bottone dopo l’altro fino a riempire il foglio.
Non si sono posti il problema di dove collocare il 3,25
Interrogati su dove collocare il 3.25 Serena risponde: Ahmed ha fatto la tabellina del due, noi volevamo fare quella del 5…ricontando…scoprono che dove era per loro il 3,25 in realtà numerando per 0,5 otteniamo il 13,25
1° VIDEO GRUPPO 1
https://drive.google.com/file/d/1CIblYhJkJmOEQi99aqphVU0CWsBjkWIG/view?usp=sharing
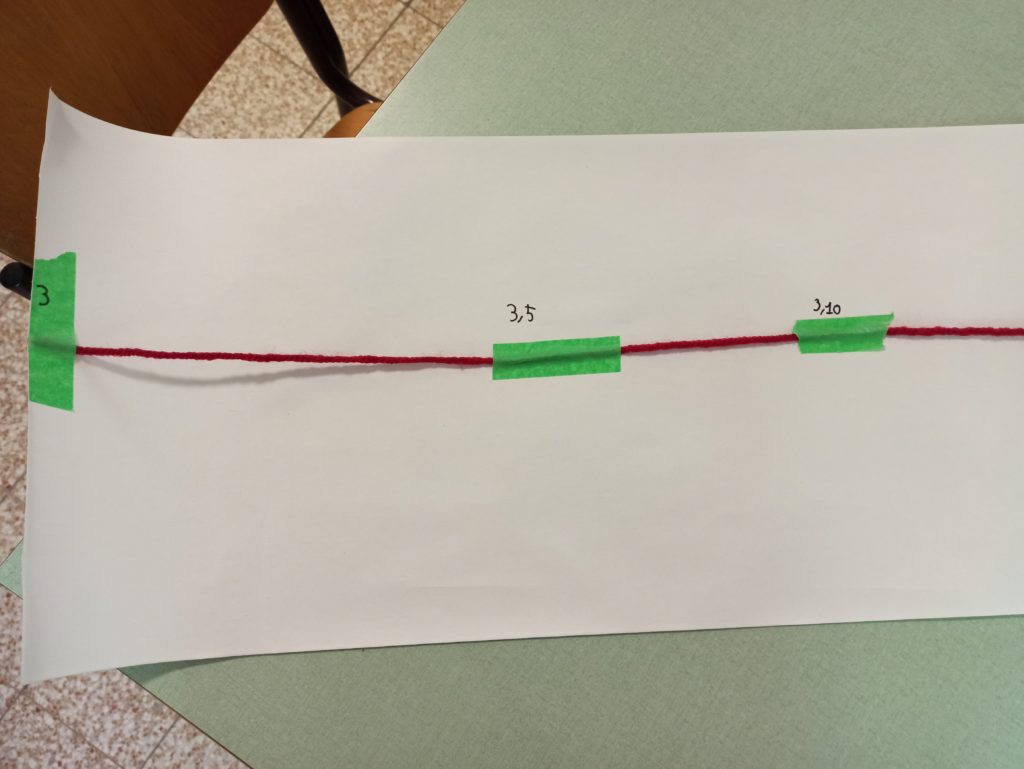
Pensano di dover smontare tutto. Gaia suggerisce di riprendere la numerazione dal 3 e conta…3…3,5…3,10,…3,15
(qui è chiaro che il modello degli interi è ancora presente e interferisce e non sanno come uscirne ovviamente, questo è l’ostacolo da superare)
2° VIDEO GRUPPO 1
https://drive.google.com/file/d/1ClW3Tnku5djAqfET1r6BYvNjuXgp0MQl/view?usp=sharing
STRISCIA CARTA CORTA
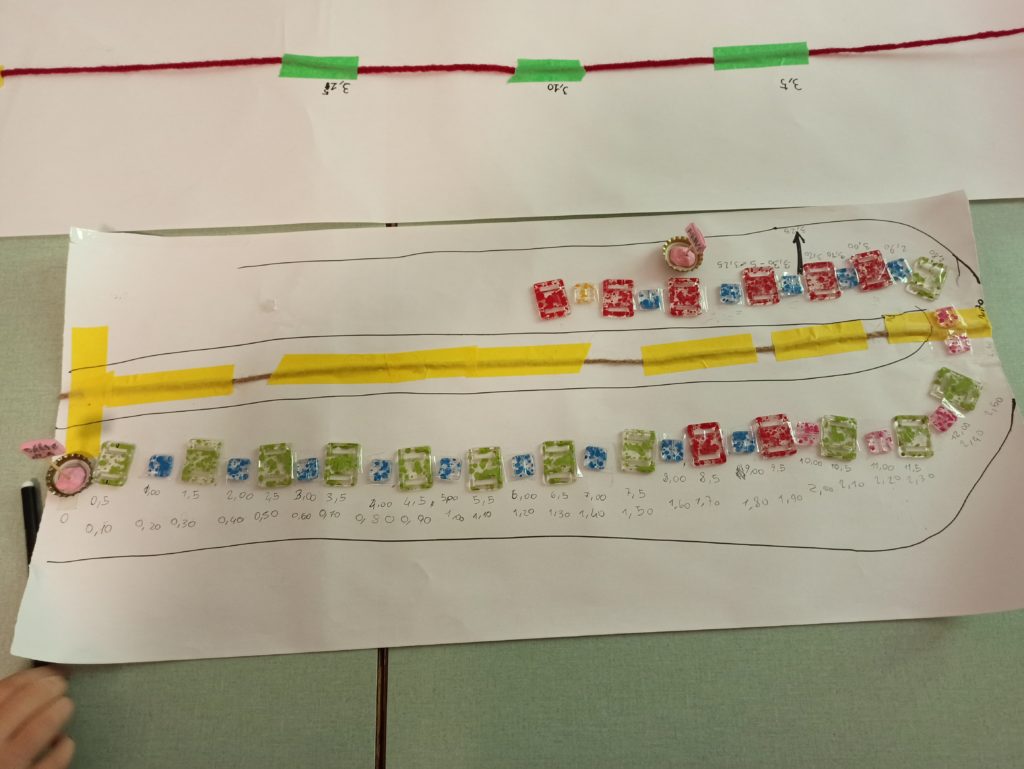
(qui c’è un bel salto concettuale perché capiscono che ci devono essere due cifre decimali per riuscire a collocare con senso il 3,25, infatti lo collocano tra 3,20 e 3,30… in realtà stanno ancora ragionando con gli interi …. permane l’ostacolo del 3,5… 3,10 ecc. testimoniato dall’altra retta ed è su questo che bisognerà lavorare, è un bell’esempio di tatônnement!!! non mi sembra che abbiano mai nominato i centesimi)
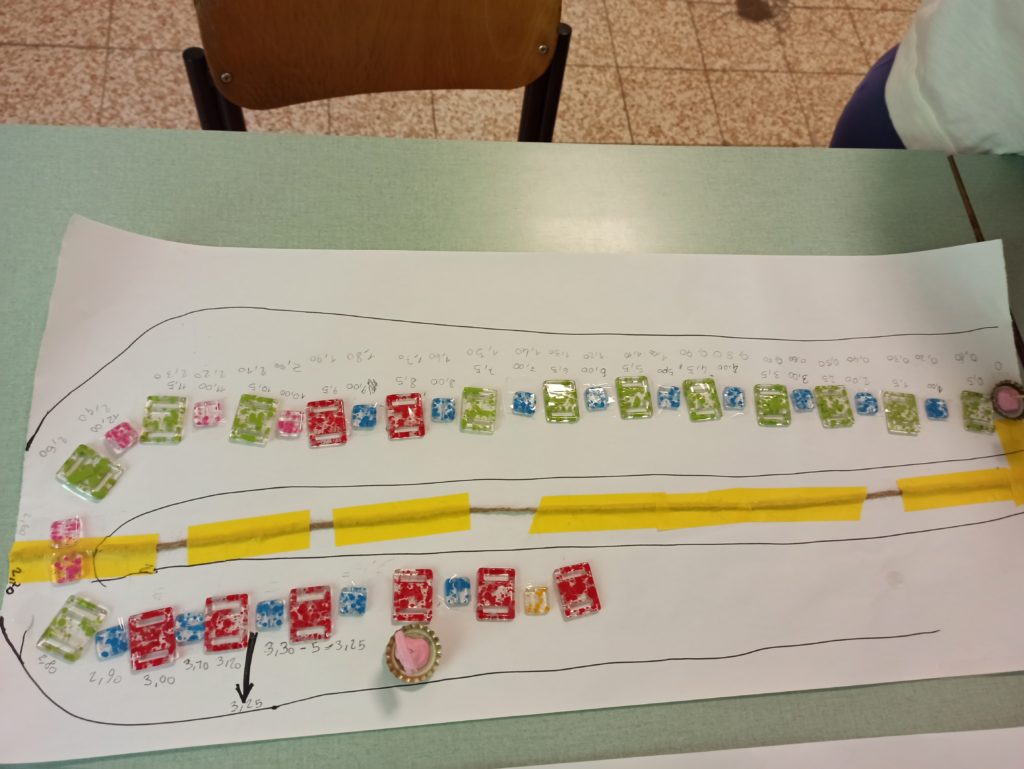
(Il problema è come far emergere chiaramente l’ostacolo in modo che il modello dei decimali cominci piano piano ad emergere)
STRISCIA DI CARTA LUNGA


GRUPPO 2
Questo gruppo è formato da due maschi e due femmine, si sono divisi i compiti e di fatto hanno lavorato a coppie. Dalila e Anita hanno lavorato sulla striscia di carta corta mentre Marco F e Iacopo hanno lavorato sulla striscia di carta lunga. Per comodità chiamo i maschi gruppo 2A e le femmine gruppo 2B.
CREAZIONE GRUPPO 2A FOTO MARCO F E IACOPO (Bravi!)


CREAZIONE GRUPPO 2B FOTO (Brave!)


(bello confrontare le due strisce, le due modalità sono interessanti e complementari)
VIDEO COSTRUZIONE STRISCIA GRUPPO 2 A
https://drive.google.com/file/d/1CRl6JwopZRlsFBAtaE9wHd_lM_XecqwI/view?usp=sharing
(qui c’è l’idea che per fare la retta ci vuole una unità di misura mentre il gruppo precedente mi sembra che andasse a occhio)
VIDEO INTRODUZIONE RETTA NUMERICA 2B E PROSECUZIONE RETTA 2A
https://drive.google.com/file/d/1CLgEXOoY3SaM_LCUhmGhLv9eyqwxbDJZ/view?usp=sharing
https://drive.google.com/file/d/1CC3Z_b1xdpCGGW13-PH_bWx6YgAX1_mG/view?usp=sharing
(il 3,25 sta dentro il 3 e il 4! Bello! 0,3 e 0,4 —- 0,25 sta in mezzo: è così?
è un quarto di centesimo…. di cento forse…)
VIDEO FINALI RETTA 2 A
https://drive.google.com/file/d/1C4x_XySC-RUJHRyM-RX6nMi4XNI_q_Gd/view?usp=sharing
ogni tacca è a 3 cm quindi 3,2 sarebbe a 6 cm e 3,25 a 6,5 per loro perché ragionano sul mezzo del centimetro successivo non sul mezzo dello spazio tra 3,2 e 3,3
(qui dai una valutazione indiretta al lavoro del bambino, quando chiedi con un certo tono “è giusto secondo te?”: risposta obbligata = no. Secondo me dovresti cercare altri punti nei filmati dove ti comporti, senza volerlo, in questo modo, così troviamo insieme dei modi alternativi)
GRUPPO 3
STRISCIA CORTA
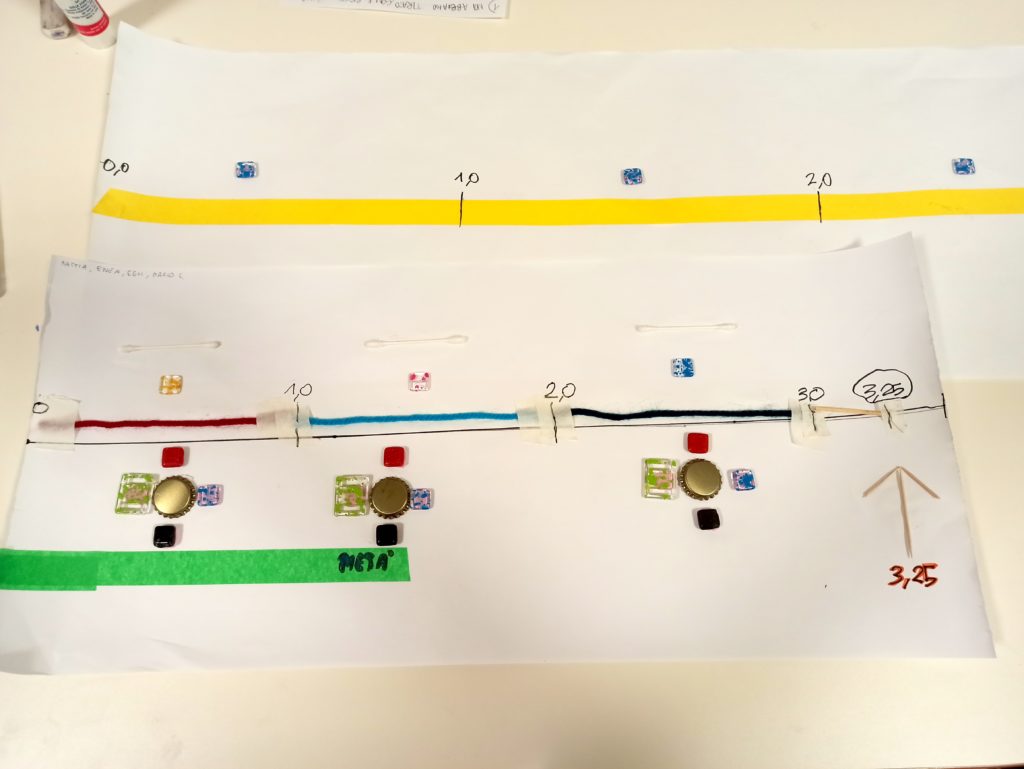
STRISCIA LUNGA


VIDEO
https://drive.google.com/file/d/1CZjABI00w0YLbCiv6j-Cs8Uq1vMcEKs_/view?usp=sharing
https://drive.google.com/file/d/1CYrJfNBPI6KvflJAww0nO_iyDUzMpWfa/view?usp=sharing
(metà della metà, 25 come 1⁄4 di 100, due grossi pivot cognitivi da sfruttare)
GRUPPO 4
STRISCIA CORTA

STRISCIA LUNGA



VIDEO
https://drive.google.com/file/d/1CBnIw1aPPcMjZKc89jjJ8nPJevKPNN-8/view?usp=sharing
Riflessioni sulla conduzione della discussione
(in grassetto i pezzi tratti dal video, in blu le possibili domande alternative dell’insegnante, in fucsia i commenti di DM, in nero normale le riflessioni dell’insegnante)
GRUPPO 1
Sere: siamo partiti dall’idea di fare una strada…
- La consegna ti chiedeva di creare una retta numerica, come mai avete deciso di disegnare una pista?
- In mezzo quali numeri scriverai?
- A che numero corrisponde ogni bottone?
- Come hai fatto a stabilire dove incollare i bottoni?
Questa è la partenza e l’arrivo è il 3,25
Serena prima conta dicendo la tabellina del 5 mettendo uno 0 davanti, ma non comprende il significato della parte decimale?!
Poi ricomincia a contare…tenendo sotto controllo i decimi e le unità
(Io penso che se non sono ancora riusciti a dare un senso a questo passaggio dai naturali ai decimali, insistere su aspetti formali non aiuta, la scomposizione del numero scritto non basta, bisogna imparare a fare spesso dei percorsi a ritroso per far recuperare i sensi mancanti, riandare alle esperienze fatte ad esempio quella delle bottiglie…)
Facciamo la tabellina del 5 – 0,5 – 0,10
Alla fine della numerazione si accorgono che l’ultimo bottone è 13,5 quindi non corrisponde a 3,25 e li faccio riflettere sul fatto che dovevano pensare prima a quanti bottoni servivano e alla corrispondenza con un determinato numero, dettata dal valore dell’intervallo tra un bottone e l’altro.
Avrei potuto chiedere dove collocare il 3,25?!
Ricomincia a contare 0 0,5 1 1,5 2……13,5

Gaia interviene suggerisce di contare 3… 3,5…. 3,10….3,15 …..3,20 (il 3,20 corrisponderebbe al 5 di Serena)
Li faccio riflettere sul fatto che Serena e Gaia stanno numerando in due modi diversi, potevo chiedere….
3,5 è quindi minore di 3,10 ? perché numerando lo hai collocato prima ? Avrebbe dovuto dire 3,05… 3,10… 3,15….
(Queste domande non aiutano superare l’ostacolo.)
Gaia non rispetta l’intervallo tra una tacca e l’altra le avrei potuto dire: Perché non scrivere 1000 al posto del 5 a questo punto?
(Pensa a che cosa potrebbe risponderti? Non è una domanda, è un tuo suggerimento che bypassa totalmente la ricerca della bambina, non tiene conto del punto a cui è, della sua vera difficoltà.)
Faccio riflettere i bambini sulla retta numerica che abbiamo in classe nella quale ogni tacca corrisponde ad un’unità, ma forzo con domande del tipo…
Io: cosa ho aggiunto?
Bambini: una unità
Io: giusto Gaia? Sei convinto Andrea?
Domande inutili a cui non possono che rispondere sì… per consolarmi!
(Secondo me il problema è che non c’è chiarezza su quale sia il vero ostacolo che la bambina deve affrontare.)
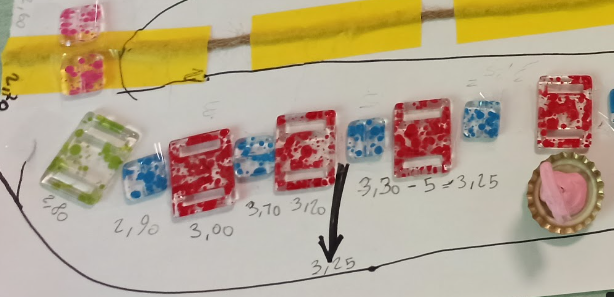
Propongo di scrivere una nuova numerazione e potevo chiedere:
- In questa nuova numerazione per quanto avete numerato?
(Continuare a farli ragionare sulle numerazioni secondo me non va bene perché rinforza ulteriormente il modello degli interi, i bambini devono dare un senso ai decimali per capire…)
- Avete scritto la seguente sottrazione:
3,30 – 5= 3,25
Il 5 (scritto così) che valore ha? Che marca mettete? Non mi sembra che aiuti il riferimento alle marche… io sono un po’ allergica a queste cose….
(Secondo me a questi bambini manca ancora un solido background su che cosa siano i numeri decimali e sul contesto in cui nascono che è quello della misura, cioè devono capire che quando si misura i naturali non bastano. Se sono ancora a quel livello, allora fare solo riferimento a questioni formali di scrittura non serve a molto. La retta dei numeri è un’astrazione ma finché si lavora dentro un contesto di senso i bambini riescono a fare dei ragionamenti più coerenti con il significato. Alcuni sono già ad un livello più astratto e quindi colgono il senso della proposta, altri hanno ancora bisogno di esperienze concrete che diano senso a quei numeri scritti sulla retta.)
Non riconoscono che il 5 ha valore di centesimo e non di unità quindi ragionano ancora con gli interi.
(Ripeto, queste sono conoscenze solo formali, quindi non avendo un significato per loro non posso costruiti sopra dei ragionamenti.)
GRUPPO 4

Ahmed: abbiamo messo il 3,25 a metà tra il 3,0 e il 3,5 perché 25 +25 fa 50… 25 sono dei centesimi
Sbagliano la misura tra 3,0 e 3,5, credo più che altro per una mancanza di spazio e per non dover rifare tutta la linea, ha messo a metà il 3,25. (risparmio energetico)
Domande possibili: prova a collocare 1,25 e 1,50 sulla retta numerica
questo avrebbe consentito di trovare la discordanza di intervallo e a trovare l’errore.
Dicendo 25+25 fa 50 …sembra che parli di unità e non di centesimi
Cosa vuol dire… virgola 25?
Cosa sono i centesimi?
Che risposte ti aspetteresti?
I centesimi sono dei numeri decimali
Le unità sono una cosa e i decimali un’altra?
Come fanno a risponderti?
Esiste la casa delle unità semplici e la casa dei decimali: millesimi, centesimi e decimi
Perché il 25 sta lì?
E’ a metà tra il 3,0 e il 3,50?
Giorgio: 25+25 fa 50
3 unità, 2 decimi e 5 centesimi
Torniamo al punto di prima…
25 significa 0,25
Qui fornisco la risposta e faccio una domanda retorica: quindi è diverso dire 25 da 0,25?
