Francesca Demartini, classe prima
Galleria di creazioni matematiche
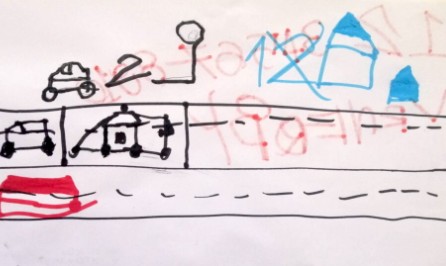










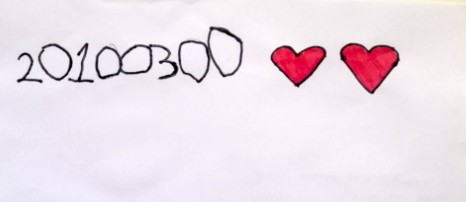
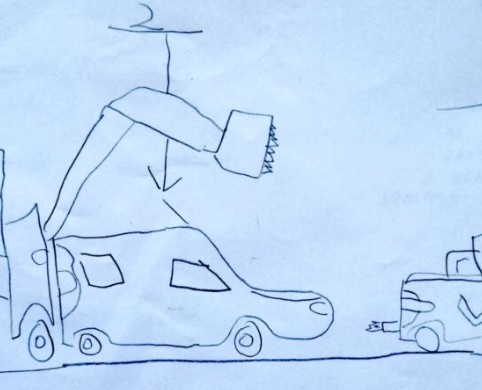



Alla ricerca di regolarità guardando la creazione di H
Partendo dal disegno di un braccialetto, abbiamo provato a realizzare il bracciale con due tipologie di pasta, indagato le strategie per contare i pezzi di pasta disposti in modo circolare (bracciale chiuso) e disposte in fila (bracciale aperto). Durante l’ultimo incontro a coppie i bambini hanno provato a realizzare nuovi bracciali aperti concordando con il compagno una regolarità nuova. (Nella discussione le lettere utilizzate per identificare i bambini sono state assegnate in modo del tutto casuale)

L’attività sulla ricerca di regolarità continua…
La creazione di H. realizzata ad ottobre ha aperto un percorso che è ancora in atto. In realtà mi succede spesso, faccio fare le creazioni e poi lavoriamo su una creazione per metà anno scolastico. Forse dovrei farne realizzare comunque delle altre, anche se il lavoro su una non è ancora terminato.
Dopo aver compreso che il bracciale di A e P era stato realizzato con la regola un pezzo di pasta in più rispetto alla posizione precedente ci siamo chiesti come fanno i matematici a scrivere uno in più, abbiamo completato la tabella per mettere in relazione il numero delle posizioni con il numero dei pezzi di pasta in ciascuna posizione e poi, sempre a coppie i bambini hanno provato a realizzare un nuovo bracciale con la seguente consegna: “E se volessimo realizzare un bracciale con la regola due pezzi di pasta in più rispetto alla posizione precedente come sarebbe?”
Abbiamo confrontato i bracciali, individuato quello che più si avvicinava a rispettare la nuova regola e abbiamo costruito una nuova tabella che poi abbiamo confrontato con quella precedente.
La scorsa settimana i bambini hanno realizzato delle creazioni, per il momento abbiamo discusso la creazione di A ma ce ne sono anche altre interessanti che magari farò discutere più avanti.
Dalla discussione della creazione di A sono emersi i seguenti aspetti:
– Quando faccio un calcolo di addizione conviene partire dal numero maggiore
– Come strategia per calcolare il risultato posso usare le dita ma anche la mente (soprattutto quando vado oltre il 10 e le dita non bastano più)
– A volte invertendo gli operatori il risultato non cambia, mentre altre volte questa inversione non si può fare. Rispetto a quest’ultimo punto mi stavo chiedendo se potrebbe aver senso far partire un ricerca in piccolo gruppo per cercare di capire se è sempre possibile invertire gli operatori di un’operazione o meno. Ora che sono fresca di formazione mi piacerebbe partire ma allo stesso tempo mi chiedo se possa essere il giusto punto di partenza per una ricerca. Inizierei con una ricerca in piccolo gruppo (magari in 3) un po’ come abbiamo provato insieme l’altro giorno, perché avendola provata in prima persona mi da’ un po’ più di sicurezza.
Commento alla discussione sulla creazione di A (D.M.)
Questa discussione è bellissima.
Ci sono tutte le strategie di calcolo e ci sono le proprietà delle operazioni.
Hai la porta aperta anche verso i numeri negativi: vediamo se superano l’idea che 3-7 non si può fare…le risorse dei bambini sono infinite. Si tratta di trovare situazioni in cui si può fare. Passerei quindi a situazioni concrete. Se ho 3 caramelle e 7 bambini 4 restano senza… 4 come differenza in negativo, 4 che mancano… se giro la situazione ho invece 4 caramelle in più…. Come indicare questi due 4 con significato diverso. Parlando di figurine una volta funzionava… debiti e crediti nello scambio… sono tutte situazioni da esplorare con tanti E se….. questa è una ricerca di tipo diverso….
La commutativa dell’addizione è ben spiegata.
Come si conta con le dita e con mente e dita insieme pure.
Farei dei cartelloni con queste scoperte.
Rimane l’addizione con i numeri grandi che richiede ulteriori abilità. Io metterei in campo del materiale concreto per contare perché verrebbe fuori la necessità di raggruppare per non perdere il conto. La ricerca qui ci sta.
Ci sono anche altri modi di usare le dita per contare numeri grandi, ad esempio usare le falangi come facevano gli antichi. Chissà se nella tua classe multiculturale ci sono esempi di modo di contare diversi magari coinvolgendo i genitori. Questo però lo farei in un secondo momento.
Addizione e sottrazione
Questa settimana ho chiesto ai bambini di ripensare a quanto era emerso dalla discussione sulla creazione di A rispetto a cosa accade quando scambio due operatori in un’operazione. Alcuni hanno iniziato a fare molti calcoli, senza però provare a invertire gli operatori, altri hanno provato a scambiarli ma rimanendo all’interno dell’addizione, scoprendo quindi che il risultato rimane sempre quello. Altri, pochi, si sono addentrati nella sottrazione provando a vedere cosa accade invertendo i numeri.
Tra quelli che hanno provato anche la sottrazione, molti hanno scritto operazioni come 8-8, 5-5 sostenendo quindi che anche con la sottrazione il risultato rimane sempre uguale invertendo i due operatori. Al momento mi sembra che sono A2 sia arrivata a pensare che quando i due numeri sono uguali, anche se li inverto nella sottrazione il risultato rimane sempre 0, se i due numeri invece sono diversi succede qualcosa di strano.
Un bambino ha provato a fare il calcolo 13+14 individuando il risultato corretto. Ha detto di essere riuscito a farlo contando un po’ con le dita e un po’ con la mente ma vorrei indagare meglio per capire come ha fatto. Prima di chiedere a E. di spiegare come ha fatto il calcolo chiederei anche agli altri di provare a farlo, con la possibilità magari di usare del materiale concreto, per poi confrontare le diverse strategie emerse.
Rispetto al lavoro sul valore posizionale stiamo contando con diversi tipi di materiale: cannucce, tessere del domino, pennarelli. Abbiamo fatto la discussione su quali possano essere delle strategie per contare più velocemente e i bambini hanno tirato fuori la conta per 2, per 3, per 4, per 5 e per 10. Le conte per 3 per 4 e per 5 sono risultate un po’ più complicate ma i bambini si sono comunque cimentati nel conteggio. Loro dicono che è più facile contare per 2 e per 10. Quindi abbiamo poi iniziato a raggruppare le cannucce con l’elastico a gruppi di 10 per contarle più velocemente. Stiamo continuando a contare quantità di cannucce riflettendo su quanti gruppi da 10 si formano, quante cannucce da sole rimangono e stiamo cercando di capire se c’è una connessione con il numero scritto.
Qualcuno inizia a intravedere una relazione tra le cifre e il numero dei gruppi da 10 e delle cannucce da sole ma continuiamo a lavorare con materiale concreto. Due anni fa con la corrispondenza con la classe di Irene ricordo che era emersa la necessità di comprendere la differenza tra i numeri 21 e 12 e questo li aveva aiutati molto a capire che le cifre erano sempre le stesse ma che posizionate in modo differente avevano valore diverso e quindi i due numeri sono diversi.
Potrei provare a proporre situazioni di vita reale per vedere cosa dicono in situazioni in cui c’è un numero piccolo meno un numero più grande.
Nel calcolo mi sembra di capire che per loro non si possa fare, perchè appunto “le dita non bastano” però in situazioni reali si possono trovare altri modi.
Scoperte su addizione e sottrazione
I bambini hanno capito che nel caso della sottrazione è importante che ci sia un numero maggiore meno un numero minore o uguale.
Nel caso di semplici sottrazioni con numero minore meno numero maggiore es. 3-5 alcuni riescono ad esplicitare il numero di dita che mancherebbero per poter eseguire l’operazione dicono “per fare 3-5 mancano ancora 2 dita”, quindi mi sembra che ci sia un po’ questa idea che l’operazione si possa eseguire in qualche modo e che il risultato non sia zero.
Ora vorrei procedere proponendo qualche situazione di vita reale e tangibile, come ad esempio ragionare sulle figurine come aveva proposto Donatella e poi chiedendo come si potrebbe trovare il risultato dell’operazione 13+14.
La documentazione che inserisco ora riguarda “come eseguire calcoli di addizione altre il 10”. I bambini si sono accorti che le dita delle mani non bastavano e hanno trovato delle strategie alternative.
A3 ho trovato un ottimo modo per eseguire il calcolo 13+14 preso dalla creazione di A1. Ricordo che l’anno scorso eravamo arrivati alla strategia di A3 il seconda, ora invece qualcuno ha capito questo metodo già in prima. Continueremo a provarlo anche con altri calcoli, oltre alle altre strategie individuate, affinchè anche i bambini che faticano, con l’aiuto dai compagni riescano a comprenderle e a farle proprie.
